代码随想录算法训练营第25天|LeetCode106.中序和后序遍历构造二叉树、LeetCode105.中序和先序遍历构造二叉树

1、LeetCode106.中序和后序遍历构造二叉树

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

知道理论怎么求，但是太久没写递归代码忘了。为了节省时间直接看视频讲解了。

思路

1. 中序遍历无法得到根节点的位置，需要从后序遍历得到。那么后序遍历的最后一个元素即根节点。
2. 但后序遍历无法得到左右区间，因此需要中序遍历。在中序中找到根节点的左右区间，进行切割。再对后序进行相应的切割。
3. 然后继续递归

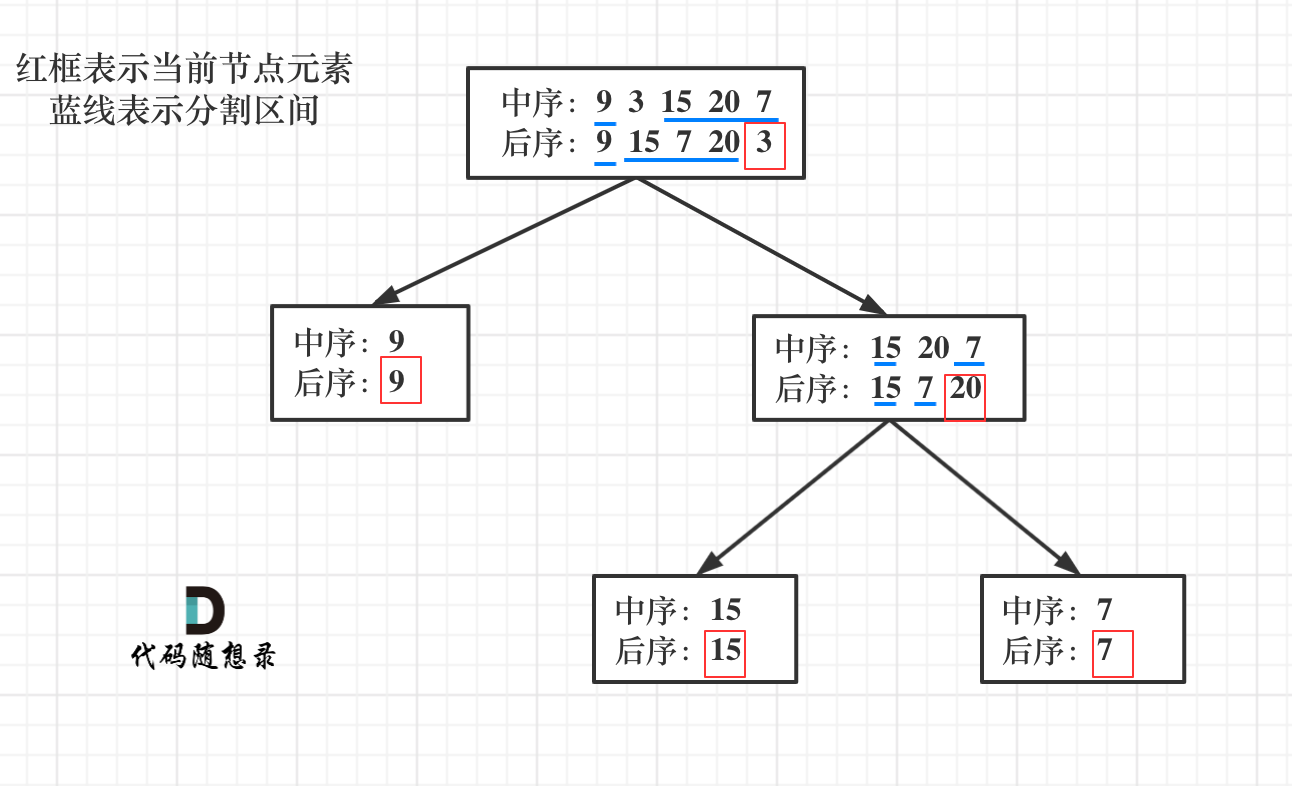
代码的步骤

1. 后序数组为空，应返回空节点
2. 后序数组只有一个元素，直接返回
3. 后序数组的最后一个元素作为节点元素
4. 寻找中序数组位置做切割点
5. 切中序数组
6. 切后序数组
7. 递归处理左右区间

代码

• 需要注意坚持“左闭右开”的原则。
• vector判断函数empty()，或者size()==0
• find(begin, end, val)按值查找，返回迭代器，减去begin即索引
• 递归的逻辑一开始没弄明白

class Solution {
public:
    TreeNode* traversal(vector<int>& inorder, int inbegin, int inend, vector<int>& postorder, int postbegin, int postend){
        // 1 为空，返回NULL
        if(postend == postbegin)    return NULL;

        // 2 只有一个元素，直接返回root
        if(postend - postbegin == 1){
            TreeNode* root = new TreeNode(postorder[postend-1]);
            return root;
        }

        // 3 找到后序遍历最后一个节点作为根节点
        TreeNode* root = new TreeNode(postorder[postend-1]);
        int rootValue = postorder[postend-1];

        // 4 切割中序遍历
        // 找到索引
        int delimiter_index = find(inorder.begin(), inorder.end(), rootValue) - inorder.begin();
        // 切割 左闭右开
        int left_in_begin = inbegin;
        int left_in_end = delimiter_index;
        int right_in_begin = delimiter_index + 1;
        int right_in_end = inend;

        // 5 切割后序遍历 左闭右开
        int left_post_begin = postbegin;
        int left_post_end = postbegin + (left_in_end - left_in_begin);
        int right_post_begin = left_post_end;
        int right_post_end = postend - 1; 

        // 6 递归处理左右区间
        root->left = traversal(inorder, left_in_begin, left_in_end, postorder, left_post_begin, left_post_end);
        root->right = traversal(inorder, right_in_begin, right_in_end, postorder, right_post_begin, right_post_end);
        return root;
        
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.empty() || postorder.empty())
            return NULL;
        return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
    }
};

2、LeetCode105.中序和先序遍历构造二叉树

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

和上一题的思路应该是一模一样的，所以可以直接改。我自己改试试

犯错：先序遍历获取根节点的时候直接取索引为0了，应该是prebegin才对。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* traversal(vector<int>& inorder, int inbegin, int inend, vector<int>& preorder, int prebegin, int preend){
        // 1 为空，返回NULL
        if(preend == prebegin)    return NULL;

        // 2 只有一个元素，直接返回root
        if(preend - prebegin == 1){
            TreeNode* root = new TreeNode(preorder[prebegin]);
            return root;
        }

        // 3 找到后序遍历最后一个节点作为根节点
        TreeNode* root = new TreeNode(preorder[prebegin]);
        int rootValue = preorder[prebegin];

        // 4 切割中序遍历
        // 找到索引
        int delimiter_index = find(inorder.begin(), inorder.end(), rootValue) - inorder.begin();
        // 切割 左闭右开
        int left_in_begin = inbegin;
        int left_in_end = delimiter_index;
        int right_in_begin = delimiter_index + 1;
        int right_in_end = inend;

        // 5 切割先序遍历 左闭右开
        int left_pre_begin = prebegin + 1;
        int left_pre_end = left_pre_begin + (left_in_end - left_in_begin);
        int right_pre_begin = left_pre_end;
        int right_pre_end = preend; 

        // 6 递归处理左右区间
        root->left = traversal(inorder, left_in_begin, left_in_end, preorder, left_pre_begin, left_pre_end);
        root->right = traversal(inorder, right_in_begin, right_in_end, preorder, right_pre_begin, right_pre_end);
        return root;
        
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(inorder.empty() || preorder.empty())
            return NULL;
        return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
    }
};