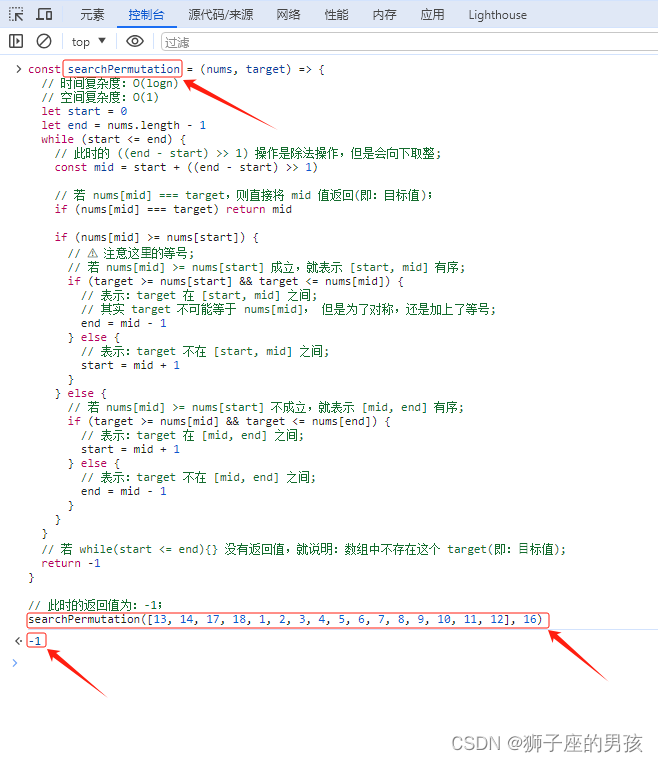
题目描述
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3 输出:-1
示例 3:
输入:coins = [1], amount = 0 输出:0
解题思路
1.贪心
1.1 想要总硬币数最少,肯定是优先用大面值硬币,所以对 coins 按从大到小排序先丢大硬币,再丢会超过总额时,就可以递归下一层丢的是稍小面值的硬币
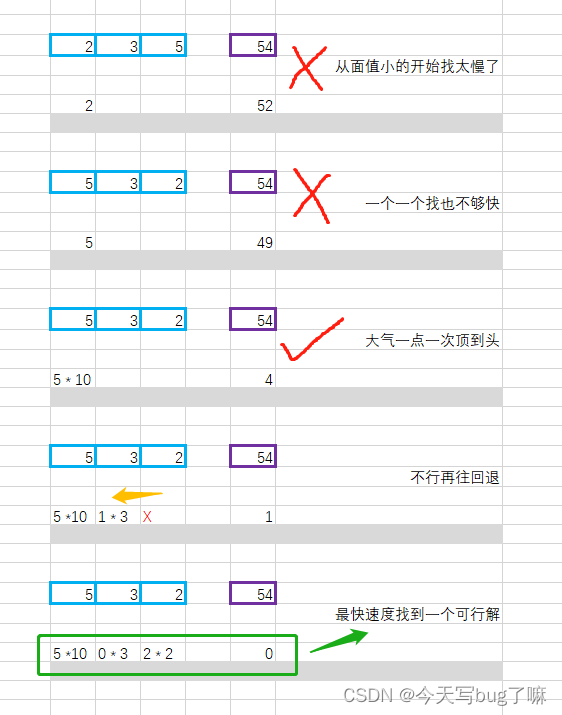
2. 乘法对加法的加速
2.1 优先丢大硬币进去尝试,也没必要一个一个丢,可以用乘法算一下最多能丢几个k = amount / coins[c_index] 计算最大能投几个
amount - k * coins[c_index] 减去扔了 k 个硬币
count + k 加 k 个硬币如果因为丢多了导致最后无法凑出总额,再回溯减少大硬币数量
3. 最先找到的并不是最优解
3.1 注意不是现实中发行的硬币,面值组合规划合理,会有奇葩情况考虑到有 [1,7,10] 这种用例,按照贪心思路 10 + 1 + 1 + 1 + 1 会比 7 + 7 更早找到
所以还是需要把所有情况都递归完
4. ans 疯狂剪枝
4.1 贪心虽然得不到最优解,但也不是没用的我们快速算出一个贪心的 ans 之后,虽然还会有奇葩情况,但是绝大部分普通情况就可以疯狂剪枝了
复杂度分析
时间复杂度:O(Sn),其中 S是金额,n是面额数。我们一共需要计算 S个状态的答案,且每个状态 F(S)由于上面的记忆化的措施只计算了一次,而计算一个状态的答案需要枚举 n个面额值,所以一共需要 O(Sn)的时间复杂度。
空间复杂度:O(S),我们需要额外开一个长为 S 的数组来存储计算出来的答案 F(S)。
代码
void coinChange(vector<int>& coins, int amount, int c_index, int count, int& ans) {
if (amount == 0) {
ans = min(ans, count);
return;
}
if (c_index == coins.size()) return;
for (int k = amount / coins[c_index]; k >= 0 && k + count < ans; k--) {
coinChange(coins, amount - k * coins[c_index], c_index + 1, count + k, ans);
}
}
int coinChange(vector<int>& coins, int amount) {
if (amount == 0) return 0;
sort(coins.rbegin(), coins.rend());
int ans = INT_MAX;
coinChange(coins, amount, 0, 0, ans);
return ans == INT_MAX ? -1 : ans;
}