摘要

知识图嵌入(Knowledge graph embedding, KGE)的目的是通过对比正负三元组，将知识图中的实体和关系映射到一个低维、密集的向量空间中。在kge的训练过程中，由于kge只包含正三元组，因此负采样对于找到高质量的负三元组至关重要。大多数现有的负抽样方法都假定不存在的高分三元组是高质量的负三元组。然而，用这些方法采样的负三元组可能包含噪声。具体来说，他们忽略了不存在的高分三元组也可能是真实事实，因为通常被称为假阴性三元组的KGs不完整。为了缓解上述问题，我们提出了一种易于插入的去噪混合方法，称为DeMix，它通过以自监督的方式精炼采样的负三元组来生成高质量的三元组。给定一个采样的未标记三元组，DeMix首先根据KGE模型本身的判断将其分类为边缘伪负三元组或负三元组。其次，为当前三元组选择合适的混合伙伴合成部分正或较硬负三元组;在知识图完成任务上的实验结果表明，本文提出的DeMix算法优于其他负采样技术，保证了相应的kge更快的收敛速度和更好的链路预测结果。

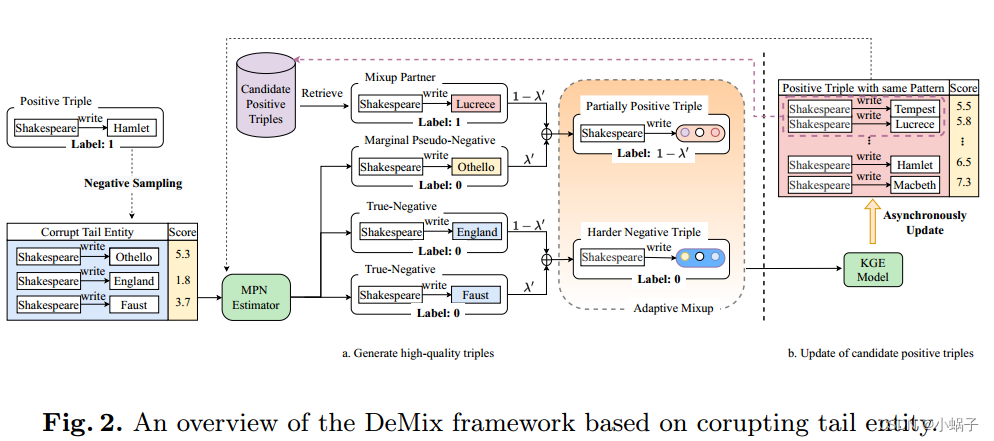 在本节中，我们将介绍提出的方法DeMix，这是一个用于生成高质量三元组的新颖且易于插入的框架。回顾采样高质量负三重组的去噪挑战，我们设计了两个模块来解决上述挑战，即边际伪负三重估计器(MPNE)和自适应混合(AdaMix)模块。MPNE模块利用KGE模型的当前预测结果将未标记的损坏三元组划分为伪负三元组和真负三元组。然后，AdaMix模块为每个损坏三元组选择合适的混合伙伴，并将它们混合在实体嵌入空间中以生成部分正确三元组或更难的负三元组，以帮助训练KGE模型。DeMix的概述如图2所示。

 

均匀采样[4]。基本的负抽样方法，即从均匀分布中抽样负三元组。

 Translating embeddings for modeling multi-relational data

伯努利抽样[24]。从考虑假负三元组的伯努利分布中抽取负三元组。

 Knowledge graph embedding by translating on hyperplanes

NSCaching[31]。NSCaching将缓存策略作为一般的负采样方案引入。

Nscaching: Simple and efficient negative sampling for knowledge graph embedding

自对抗抽样[18]。它利用自评分函数，并根据当前的嵌入模型对负三元组进行采样。

Rotate: Knowledge graph embedding by relational rotation in complex space

RW-SANS[1]。它利用图结构从节点邻域的k-hop中抽取负三元组。

Structure aware negative sampling in knowledge graphs.

CANS[16]。CANS是CAKE[16]的一个组成部分，负责解决无效的负采样挑战。考虑到我们的方法侧重于KGEs的负采样，我们主要比较CANS而不是CAKE。

Cake: A scalable commonsense-aware framework for multi-view knowledge graph completion

ESNS[29]。它考虑了实体之间的语义相似性来解决假阴性样本的问题

 Entity similarity-based negative sampling for knowledge graph embedding