- 采集到原始的数据中会存在一些噪点数据,噪点数据是对分析无意义或者对分析起到偏执作用的数据。
- 如何清洗:
- 清洗空值/缺失值
- 清洗重复值
- 清洗异常值
import pandas as pd
from pandas import DataFrame,Series
import numpy as np
pandas处理空值操作
- isnull
- notnull
- any
- all
- dropna
- fillna
df = DataFrame(data=np.random.randint(0,100,size=(7,5)))
df.iloc[0,3] = np.nan
df.iloc[3,3] = None
df.iloc[2,2] = np.nan
df.iloc[5,3] = np.nan
df
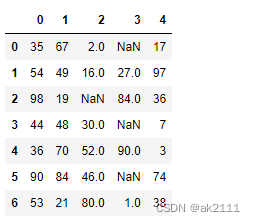
-
缺失值的处理方案:
- 1.可以将空值对应的行/列进行删除
- 2.可以将空值进行填充
-
将空值对应的行进行删除
ret = df.isnull() #可以通过isnull判断df中是否存在空数据
ret

#监测ret中哪些行存在True(表示df中哪些行存在空值)
ex = ret.any(axis=1) #axis=1表示轴向为行
#any可以对ret表格中的行进行是否存在True的判定,如果存在True,则给该行返回一个True,否则返回False
ex

#整合后的结果;在df中True对应的行是存在空值
ex = df.isnull().any(axis=1)
ex

ex = df.notnull().all(axis=1) #all判断每一行中是否全部为True,如果全部为True,则给该行返回True,否则返回False
ex

df.loc[ex] #一般可以将notall->all返回的结果作为df的行索引,过滤空对应的行数据
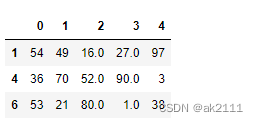
#更简单的过滤空对应的行数据的方式
df.dropna(axis=0) #注意在dropna中的轴向0表示行,1表示列
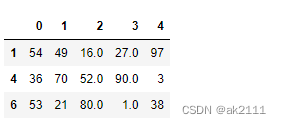
#需求:知道df中每一列存在空值的个数/占比
for col in df.columns:
#col表示df的某一列的列索引
#判断列中是否存在空值
if df[col].isnull().sum() > 0:
#计算空值占比
p = df[col].isnull().sum() / df[col].size
#将p小数转换成百分比显示
p = format(p,‘.2%’) #.2%表示将p转换成保留2位小数的百分数
print(col,‘列中存在的空值的占比为:’,p)

- 将空值进行填充
#使用任意值对空值进行填充
df.fillna(value=666) #将df中所有的空值填充为666
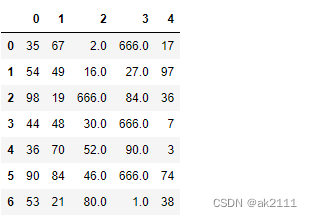
#使用有意义的数据对空值进行填充(近邻值)
df.fillna(method=‘bfill’,axis=0) #在竖直方向上选择空后面的元素填充空值
#method填充方式:ffill(向前填充)和bfill(向后填充)
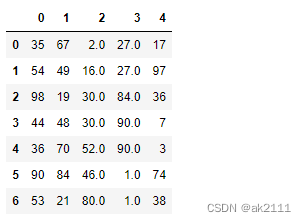
#使用有意义的数据对空值进行填充(统计值)
#使用列的均值填充列的空值
for col in df.columns:
if df[col].isnull().sum() > 0:
mean_value = df[col].mean()
df[col].fillna(value=mean_value,inplace=True)
df
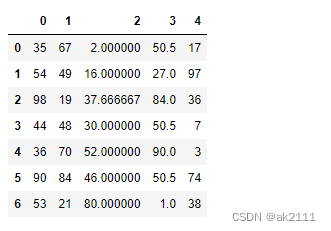
- 注意:实现空值的清洗最好选择删除的方式,如果删除的成本比较高,再选择填充的方式。
处理重复数据
- 基于duplicated和drop进行删除重复行操作
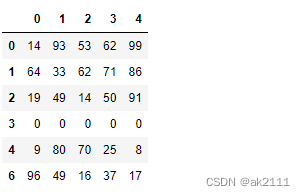
df = DataFrame(data=np.random.randint(0,100,size=(8,5)))
df.iloc[3] = [0,0,0,0,0]
df.iloc[5] = [0,0,0,0,0]
df.iloc[7] = [0,0,0,0,0]
df
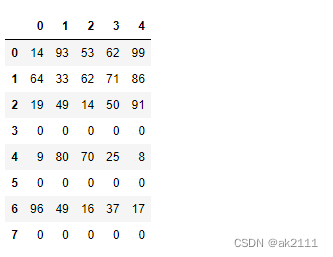
#如何监测数据中是否存在重复的行数据
df.duplicated() #可以监测原始数据中哪些行是重复,重复则返回True,否则返回False

df.duplicated().sum() #说明df这组数据中有2行重复的行数据
2
df.drop_duplicates(inplace=True) #直接删除数据中重复的行数据
df
处理异常/离群数据
异常值是分析师和数据科学家常用的术语,因为它需要密切注意,否则可能导致错误的估计。简单来说,异常值是一个观察值,远远超出了样本中的整体模式。
异常值在统计学上的全称是疑似异常值,也称作离群点(outlier),异常值的分析也称作离群点分析。异常值是值样本中出现的’极端值’,数据值看起来异常大或异常小,其分布明显偏离其余的观测值。异常分析是检验数据中是否存在不合常理的数据,在数据分析中,既不能忽视异常值的存在,也不能简单地把异常值从数据分析中剔除。重视异常值的出现,分析其产生的原因,常常成为发现新问题进而改进决策的契机。
举个例子,做客户分析,发现客户的年平均收入是80万美元。但是,有两个客户的年收入是4美元和420万美元。这两个客户的年收入明显不同于其他人,那这两个观察结果将被视为异常值。
- 给定条件的异常数据处理
- 自定义一个1000行3列(A,B,C)取值范围为0-1的数据源,然后将C列中的值大于其两倍标准差的异常值进行清洗
import pandas as pd
from pandas import DataFrame
import numpy as np
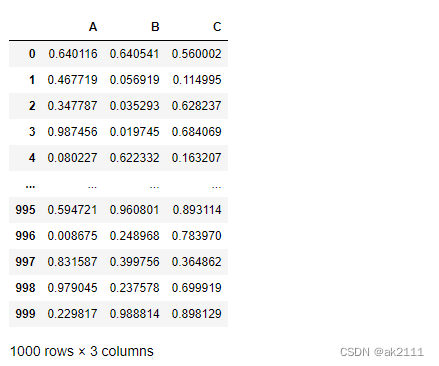
data = DataFrame(data=np.random.random(size=(1000,3)),columns=[‘A’,‘B’,‘C’])
data
#求出了C列数据的2倍标准差
twice_std = data[‘C’].std() * 2
twice_std
0.5816897093856236
ex = data[‘C’] > twice_std
data.loc[ex] #取出了异常值对应的行数据

indexs = data.loc[ex].index #取出了异常值对应行数据的行索引
indexs

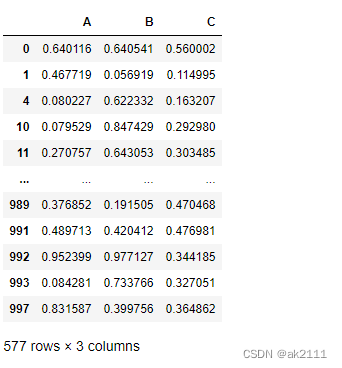
data.drop(index=indexs,inplace=True) #在演示数据中将异常值对应的行数据进行清洗
data
- 标准差法
- 又称拉依达准则(标准差法),对某些异常数据进行剔除,以提高数据的准确性。
- 适用场景:
- 仅局限于对正态或近似正态分布的样本数据处理,且数据量级尽可能大会更加使用。
- 工作原理:
- 先假设一组检测数据存在异常数据,对其进行计算处理得到标准偏差σ,然后确定一个区间,认为凡超过这个区间的就是异常数据,则对该数据予以剔除。
- 标准差本身可以体现因子的离散程度,是基于因子的平均值μ而定的。在离群值的处理过程中,可通过μ ± nσ来衡量因子与平均值的距离(n通常使用3)。
- 将区间[μ - 3σ,μ + 3σ]的值视为正常值范围,在[μ - 3σ,μ + 3σ]外的值视为离群值。
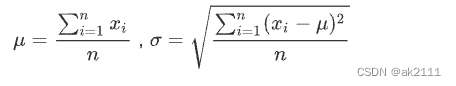
- 将区间[μ - 3σ,μ + 3σ]的值视为正常值范围,在[μ - 3σ,μ + 3σ]外的值视为离群值。
#伪造了一组含有5个异常数据的样本
iris_length = abs(np.random.randn(9999))
#手动添加一些异常数据
iris_length[44] = 54
iris_length[33] = 67
iris_length[22] = 56
iris_length[11] = 87
iris_length[55] = 49
iris_length
def std_opt(data):
mean_value = data.mean()#均值
std_value = data.std() #标准差
m_min = mean_value - 3 * std_value
m_max = mean_value + 3 * std_value
return m_min,m_max
m_min,m_max = std_opt(iris_length)
for i in iris_length:
if i < m_min or i > m_max:
print(i)
87.0
56.0
67.0
54.0
49.0
- MAD法
-
又称为绝对值差中位数法,是一种先需计算所有因子与中位数之间的距离总和来检测离群值的方法,使用大样本数据
-
公式:设有平稳离散数据X=[x1,x2,…,xn],其数据中位数为X_median:

-
应用场景:
- 当数据呈对称分布或接近对称分布时MAD和标准差法效果相等或接近相等
- 当数据为偏态分布,应选择众数或中位数等位置代表值,这时它们的代表性要比均值好。
-
def median_opt(data):
median = np.median(data)
count = data.size
a = (((data-median)**2).sum()/count)**0.5
m_min = median - 3 * a
m_max = median + 3 * a
return m_min,m_max
median_opt(iris_length)
(-3.9479897059920868, 5.302663263389095)
m_min,m_max = median_opt(iris_length)
for i in iris_length:
if i < m_min or i > m_max:
print(i)
87.0
56.0
67.0
54.0
49.0
源文件可在这里下载:
https://download.csdn.net/download/ak2111/89025242?spm=1001.2014.3001.5501