学习流程

————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————
整数在内存里面的存储
整数在计算机里面的存储的方式的大纲普及
整数在计算机里面的存储是按照二进制的方式进行存储
显示的时候是按照16进制的方法进行显示
1. 整数在内存中的存储在讲解操作符的时候,我们就讲过了下⾯的内容:整数的2进制表⽰⽅法有三种,即原码、反码和补码
三种表⽰⽅法均有符号位和数值位两部分,符号位都是⽤0表⽰“正”,⽤1表⽰“负”,⽽数值位最⾼位的⼀位是被当做符号位,剩余的都是数值位。
正整数的原、反、补码都相同。负整数的三种表⽰⽅法各不相同。
原码:直接将数值按照正负数的形式翻译成⼆进制得到的就是原码。
反码:将原码的符号位不变,其他位依次按位取反就可以得到反码。
补码:反码+1就得到补码。
对于整形来说:数据存放内存中其实存放的是补码。
总结
在计算机系统中,整数的存储使用的是补码形式,而不是原码,计算的形式是原码,而不是补码。
原码转补码需要取反+1
补码转原码也需要取反+1
实际的存储不管怎么说都是二进制,但是为了观察方便,采取的是16进制的方式进行表现
———————————————————————————————————————————
详解
为什么呢?在计算机系统中,数值⼀律⽤补码来表⽰和存储。原因在于,使⽤补码,可以将符号位和数值域统⼀处理;同时,加法和减法也可以统⼀处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
———————————————————————————————————————————
1. 数据类型
计算机中整数类型有多种,常见的有短整型(short)、整型(int)、长整型(long)等。这些类型定义了整数能表示的范围以及所占用的内存空间。例如,在C语言中,short通常占用2个字节(16位),int通常占用4个字节(32位),long在某些平台上是4个字节,在64位系统上可能是8个字节。
———————————————————————————————————————————
2. 字节大小
字节是计算机存储的基本单位,一个字节(byte)包含8位(bit)。因此,一个字节可以表示256(2^8)个不同的值,从0到255。整数的大小取决于它占用的字节数。
———————————————————————————————————————————
3. **Endianness(字节序)**:
这指的是多字节数据在内存中的存储顺序。有两种主要的字节序:小端(little-endian)和大端(big-endian)。在小端格式中,最小的字节存储在地址最低的位置,而在大端格式中,最大的字节存储在最低地址。不同的硬件和操作系统可能使用不同的字节序。
———————————————————————————————————————————
4. **整数的表示方法**:
整数在内存中的存储方法依赖于整数的类型和大小。
- 对于有符号整数,通常使用二进制补码(two's complement)表示法。这种方法允许一个数表示正数和负数,并且可以简化算术运算的硬件实现。
- 无符号整数则直接以二进制形式存储,不使用补码。
例如,一个32位的整数(int)可以表示从-2,147,483,648到2,147,483,647范围内的任何整数。存储时,计算机将这些数字转换为二进制形式,并按照机器的字节序排列。在内存中,这些二进制数会被分成4个字节,每个字节8位,按照特定的顺序(取决于系统的endianness)存储。
总之,整数在内存中的存储涉及数据类型、字节序以及二进制补码或无符号表示法,这些因素共同决定了如何在计算机内存中为整数分配空间以及如何解读这些空间中的数据。
————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————
大小端字节序和字节序的判断+有符号整形和无符号整形的取值范围
大小端存在的意义
大小端字节存储方式(Big-Endian 和 Little-Endian)的存在主要是由于不同计算机体系结构和网络通信标准对数据表示方式的差异所导致的。大小端字节存储方式的存在具有以下意义:
1. 兼容性:不同的计算机系统和网络协议可能采用不同的字节顺序。大小端字节存储方式允许不同系统之间的数据交换和通信,只要各方都遵守相同的字节顺序约定。
2. 性能:在某些计算机体系结构中,例如x86架构,小端字节存储方式有助于优化性能,因为处理器通常从最低地址开始访问数据,这与小端字节顺序相匹配。
3. 历史原因:早期的一些计算机系统(如IBM的System/360系列)采用了大端字节存储方式,而其他系统(如 Motorola 68000系列)则采用了小端字节存储方式。这些早期的设计选择在后来的技术发展中继续被一些新的系统采用。
4. 可移植代码:在编写可移植的代码时,程序员需要考虑字节顺序的问题,并可能需要使用字节交换或掩码操作来确保代码在不同的系统上都能正确运行。
5. 数据交换:在网络通信和数据交换中,大小端字节顺序的正确处理确保了数据的正确解释。例如,TCP/IP协议栈中的数据包需要按照网络字节顺序(Big-Endian)来处理。
6. 架构设计:计算机体系结构的设计者可以根据系统内部的数据处理方式来选择合适的字节顺序,以便于实现高效的数据访问和处理。
总之,大小端字节存储方式的存在是为了适应不同的系统设计、通信协议和性能需求。正确处理字节顺序对于确保数据的一致性和正确性至关重要。———————————————————————————————————————————
什么是大小端
大小端(Big-Endian 和 Little-Endian)是指计算机系统中多字节数据类型的存储顺序。这种存储方式影响数据的读取和写入,特别是对于有符号整数和浮点数的字节顺序。
1. 大端
- 在大端字节存储方式中,数据的高位字节(Most Significant Byte,MSB)存储在内存的低地址端,而低位字节(Least Significant Byte,LSB)存储在内存的高地址端。
- 例如,对于一个四个字节的整数305419896(二进制为00110000 00001010 00001001 00001000),在Big-Endian系统中,它会被存储为:0011 0000 0000 1010 0000 1001 0000 1000。
2. 小端
- 在小端字节存储方式中,数据的低位字节(LSB)存储在内存的低地址端,而高位字节(MSB)存储在内存的高地址端。
- 继续上面的例子,在Little-Endian系统中,整数305419896会被存储为:0000 1000 0000 1001 0000 1010 0000 1000。
字节顺序对于二进制数据的处理非常重要,特别是在涉及到网络传输和不同计算机体系结构之间的数据交换时。网络传输通常遵循Big-Endian字节顺序,而某些计算机体系结构(如x86架构)使用的是Little-Endian字节顺序。
程序员在处理跨平台或跨网络的数据时,需要考虑字节顺序的差异,并可能需要进行相应的转换。在编程语言中,有一些函数库或方法可以帮助开发者处理字节顺序的转换。例如,在C语言中,可以使用`memcpy`函数来复制内存块,而`htons`、`htonl`、`ntohs`和`ntohl`函数用于网络字节顺序与主机字节顺序之间的转换。———————————————————————————————————————————
简单的说就是
什么是⼤⼩端?
其实超过⼀个字节的数据在内存中存储的时候,就有存储顺序的问题,按照不同的存储顺序,我们分为⼤端字节序存储和⼩端字节序存储,下⾯是具体的概念:
⼤端(存储)模式:是指数据的低位字节内容保存在内存的⾼地址处,⽽数据的⾼位字节内容,保存在内存的低地址处。
⼩端(存储)模式:是指数据的低位字节内容保存在内存的低地址处,⽽数据的⾼位字节内容,保存在内存的⾼地址处。上述概念需要记住,⽅便分辨⼤⼩端。———————————————————————————————————————————
具体举例
小端存储 在内存里面的存储是倒过来的

那么大端的存储在内存里面是按照顺序进行存储的
也就是顺着存储也就是大端存储,逆着存就是小端存储
———————————————————————————————————————————
图解
首先我们知道 在计算机的存储里面
如果你给一个类型是int类型,那么这个是四个字节
这四个字节是按照大小端进行存储的,
这里如果我们给一个数值1
存放在数值里面那么
如果是小端存储 此时在监视内存里面可以看到四个字节的排序方式是 01 00 00 00 (逆着存储)
如果是大端存储 此时在监视内存里面可以看到四个字节的排序方式是 00 00 00 01(顺序存储)
如果我们按照逻辑进行推论 那么

首先 我们是知道的是
地址是从低地址到高地址累计的
字节的高位和低位
是从右到左 依次是个十百千万
所以我们得知 123里面 ,1是个位也就是低位,3是百位也就是高位
同理我们上述图推理出来
小端字节序存储:低位字节放到低地址处,高位字节放到高地址处。
大端字节序存储:高位字节放在低地址处,低位字节放到高地址处。
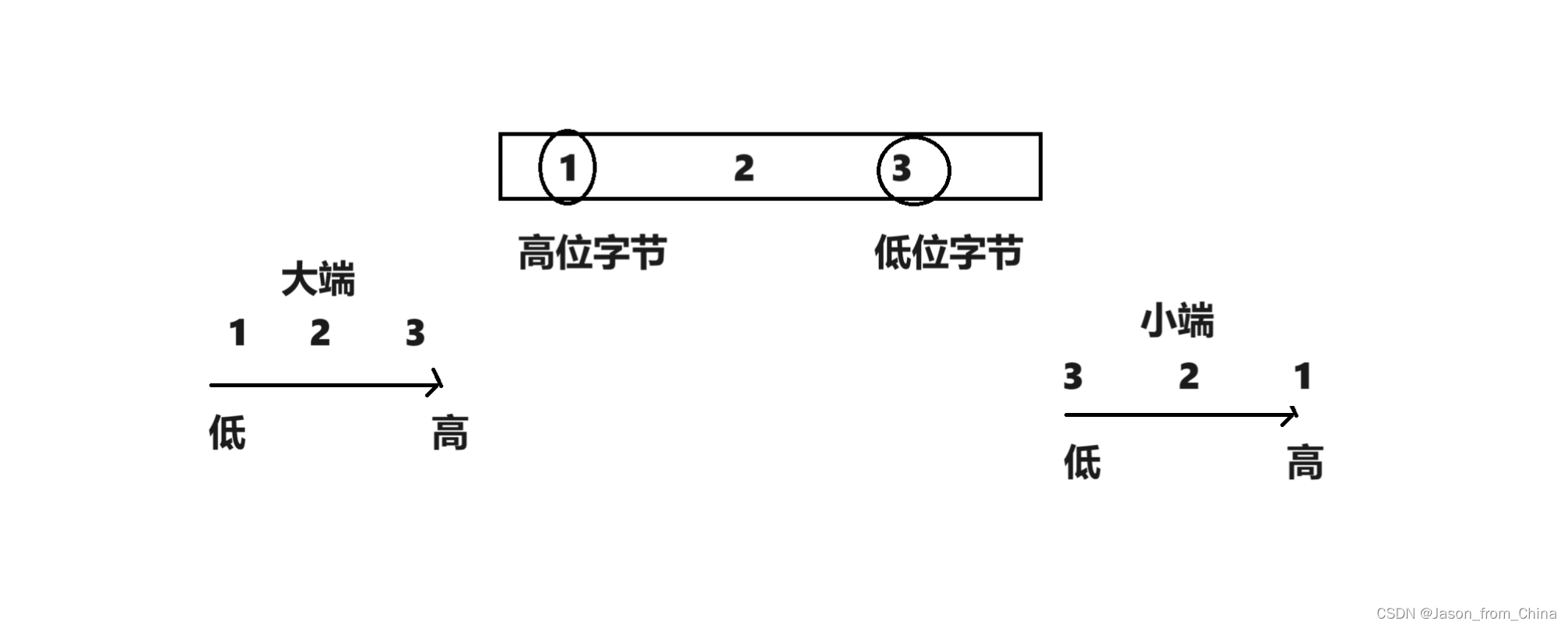
小端字节序(Little-Endian)和大端字节序(Big-Endian)是两种不同的字节存储顺序方式,它们在多字节数据类型(如整数、浮点数等)的存储上存在差异:
- **小端字节序(Little-Endian)**:在小端字节序中,数值的最低位字节被存储在最低的地址中,而最高位字节被存储在最高的地址中。换句话说,数据的高位字节到低位字节是按照地址从低到高进行存储的。这种存储方式在现代计算机体系结构中较为常见,包括x86、ARM等处理器。
- **大端字节序(Big-Endian)**:在大端字节序中,数值的最高位字节被存储在最低的地址中,而最低位字节被存储在最高的地址中。这意味着数据的高位字节到低位字节是按照地址从高到低进行存储的。这种存储方式在一些早期的计算机系统中较为常见,例如IBM的System/360。
在网络通信中,通常使用大端字节序来保证数据的统一性和可交换性。例如,IP地址、端口号、网络字节顺序(如UTF-8编码的字符串)等都是使用大端字节序进行存储和传输的。
在编程中,操作系统和编译器通常会处理字节序的问题,但在跨平台编程或网络编程中,程序员可能需要手动进行字节序的转换,以确保数据在不同系统或网络之间正确地传输和解读。
———————————————————————————————————————————
为什么会有⼤⼩端模式之分呢?以及大小端会怎么出现。
这是因为在计算机系统中,我们是以字节为单位的,每个地址单元都对应着⼀个字节,⼀个字节为8bit位,但是在C语⾔中除了8bit的 char 之外,还有16bit的 short 型,32bit的 long 型(要看具体的编译器),另外,对于位数⼤于8位的处理器,例如16位或者32位的处理器,由于寄存器宽度⼤于⼀个字节,那么必然存在着⼀个如何将多个字节安排的问题。因此就导致了⼤端存储模式和⼩端存储模式。
例如:⼀个 16bit 的 short 型 x ,在内存中的地址为 0x0010 , x 的值为 0x1122 ,那么0x11 为⾼字节, 0x22 为低字节。对于⼤端模式,就将 0x11 放在低地址中,即 0x0010 中,0x22 放在⾼地址中,即 0x0011 中。⼩端模式,刚好相反。我们常⽤的 X86 结构是⼩端模式,⽽KEIL C51 则为⼤端模式。很多的ARM,DSP都为⼩端模式。
有些ARM处理器还可以由硬件来选择是⼤端模式还是⼩端模式。
也就是一般情况下 x86也就是小端模式
⽽KEIL C51 则为⼤端模式
———————————————————————————————————————————
大小端的练习1
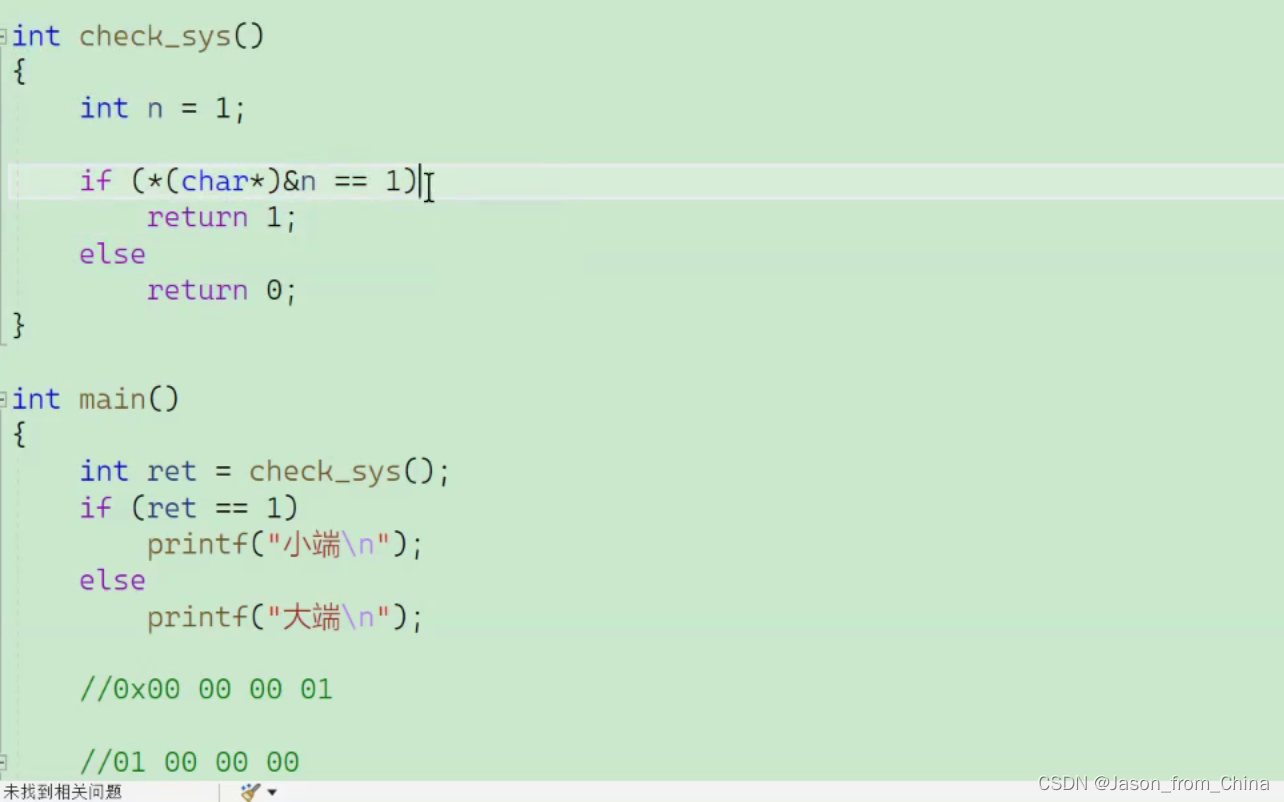
练习1 设计一个小程序 判断大小端
这里必须拿到a的地址 然后向后四个字节 直接只是强制类型是不行的

或者
简化
强制类型转化是先按出来 然后拿出最后一个字节

n的地址取出来是int*
但是我想访问一个字节不是四个字节
所以强制类型转化 指向第一个字节
这里补充一下 如果强制类型转化的时候 直接进行强制类型转化 长字节转化为短字节 此时也就是只取最后一个

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//判断大小端
int main()
{
int a = 1;//首先这里给出一个数值
//这里需要进行强制类型转化 为什么呢
// 因为这里给出的是一个整形 内存的存储是一个字节 一个字节进行存储的 也就是
//大端:00 00 00 01
//小端:01 00 00 00
//此时我们不知道这个编译器是大端 还是小端 所以 此时需要我们进行判断
//假设是小端 此时我们取地址取出的是整个int类型的 首元素的地址 不是单独指向 四个字节大小的其中一个字节
//所以我们需要进行强制类型转化 强制转化为 一个字节的类型
//同时因为这里是取地址 需要用指针进行接收
//所以我们强制类型转化为char*类型
//同时他是一个指针 取出a的地址 是一个指针 从而判断第一个字节是00 还是01 从而判断是不是大小端
if (*(char*)&a == 1)
{
printf("小端");
}
else
{
printf("大端");
}
return 0;
}
———————————————————————————————————————————
大小端的练习2
代码
#include <stdio.h>
int main()
{
char a= -1;
signed char b=-1;
unsigned char c=-1;
printf("a=%d,b=%d,c=%d",a,b,c);
return 0;
}代码的讲解
首先我们需要知道
整形在内存的存储是补码储存,原码进行计算,补码进行存储
正数原码反码补码是一样的
负数的原码需要取反+1
所以也就是
这里计算是需要补满32位的 因为int类型是4个字节 也就是32比特位
在进行转化之后 因为是char类型的 所以需要进行整形截断
然后 打印的时候再进行整形提升
char a= -1;
进行计算
//因为是负数 所以首位是1
//10000000 00000000 00000000 00000001这里是补码 但是我们计算需要进行原码进行计算 所以
//11111111 11111111 11111111 11111110这里是反码 反码就是除了符号位 其他都是按位取反
//11111111 11111111 11111111 11111111这里计算出原码 反码+1 也就是原码
//11111111 最后因为是char类型的 产生截断 只保留 一个字节 也就是八个比特位
//最后打印的时候要进行整形提升 因为是打印的是整数 所以按照符号位进行整形提升
//所以也就是
//11111111 11111111 11111111 11111111
signed char b=-1;
//这里是有符号整形
//所以这里是计算方式是一样是 也就是
//因为是负数 所以首位是1
//10000000 00000000 00000000 00000001这里是补码 但是我们计算需要进行原码进行计算 所以
//11111111 11111111 11111111 11111110这里是反码 反码就是除了符号位 其他都是按位取反
//11111111 11111111 11111111 11111111这里计算出原码 反码+1 也就是原码
//11111111 最后因为是char类型的 产生截断 只保留 一个字节 也就是八个比特位
//最后打印的时候要进行整形提升 因为是打印的是整数 所以按照符号位进行整形提升
//所以也就是
//11111111 11111111 11111111 11111111
unsigned char c=-1;
//这个是无符号整形
//无符号整形的计算方式很有意思
//无符号整数的计算方式前面换算的时候是按照负数进行换算的 也就是
//10000000 00000000 00000000 00000001原码
//11111111 11111111 11111111 11111110反码
//11111111 11111111 11111111 11111111补码
//11111111截断
//此时有意思的来了
//因为的无符号整形 所以整形提升的时候 他补的符号位是0
//也就是
//00000000 00000000 00000000 11111111
//所以也就是255的数值
//也就是说
// c 的二进制表示(补码)为 11111111(最高位为 1,但是因为是无符号类型,不进行符号位的判断)
// 当打印 c 时,直接打印出其数值,即 255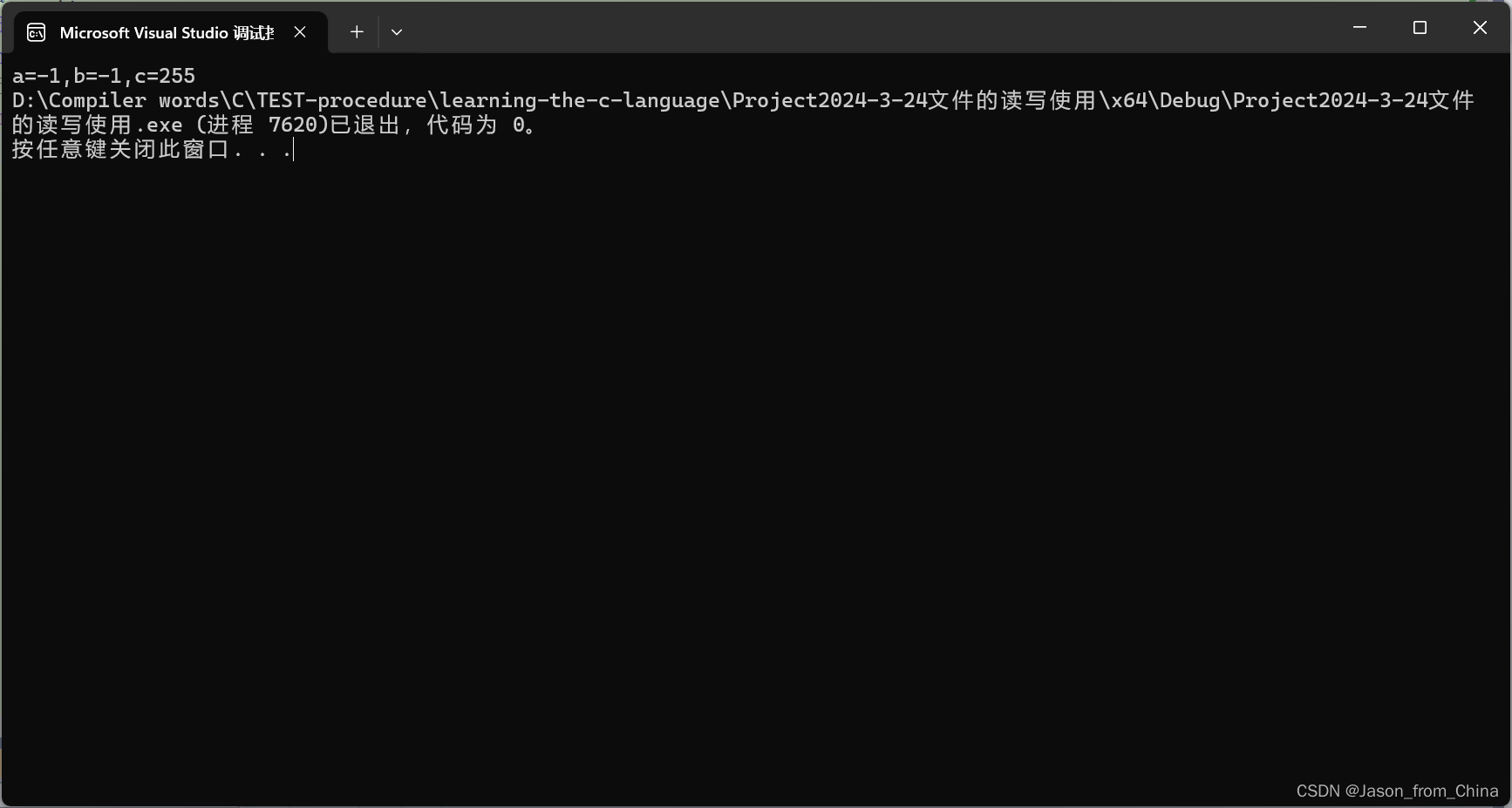 关于大小端的问题 需要知道 大小端本质是计算机是一种存储方式
关于大小端的问题 需要知道 大小端本质是计算机是一种存储方式
拿出来使用的时候也就没有大小端的问题
让你看的时候才有大小端的问题
不理解整形提升的 可以看一下这个博客
整形提升和算数转换-CSDN博客![]() https://blog.csdn.net/Jason_from_China/article/details/135875481
https://blog.csdn.net/Jason_from_China/article/details/135875481
———————————————————————————————————————————
大小端的练习2 知识点的补充
有符号整形和和无符号整形的取值区间
这里是画图是有符号整形和无符号整形的取值范围
在 C 语言中,整数类型分为有符号整数和无符号整数,它们的取值范围如下:
有符号整数:
- `signed char`:取值范围是从 -128 到 127。
- `short`:取值范围是从 -32768 到 32767。
- `int`:取值范围是从 -2147483648 到 2147483647。
- `long`:取值范围取决于编译器的实现,通常是 -2147483648 到 2147483647 或者更大。
- `long long`:取值范围是从 -9223372036854775808 到 9223372036854775807。
无符号整数:
- `unsigned char`:取值范围是从 0 到 255。
- `unsigned short`:取值范围是从 0 到 65535。
- `unsigned int`:取值范围是从 0 到 4294967295。
- `unsigned long`:取值范围取决于编译器的实现,通常是 0 到 4294967295 或者更大。
- `unsigned long long`:取值范围是从 0 到 18446744073709551615。
需要注意的是,这些取值范围是在标准状况下,具体实现的取值范围可能会因为编译器的不同而有所差异。此外,`int` 类型通常会被推广(promoted)到 `long` 类型,而 `long` 类型会被推广到 `long long` 类型,当进行这些类型转换时,取值范围也会相应改变。
有符号整形的图解
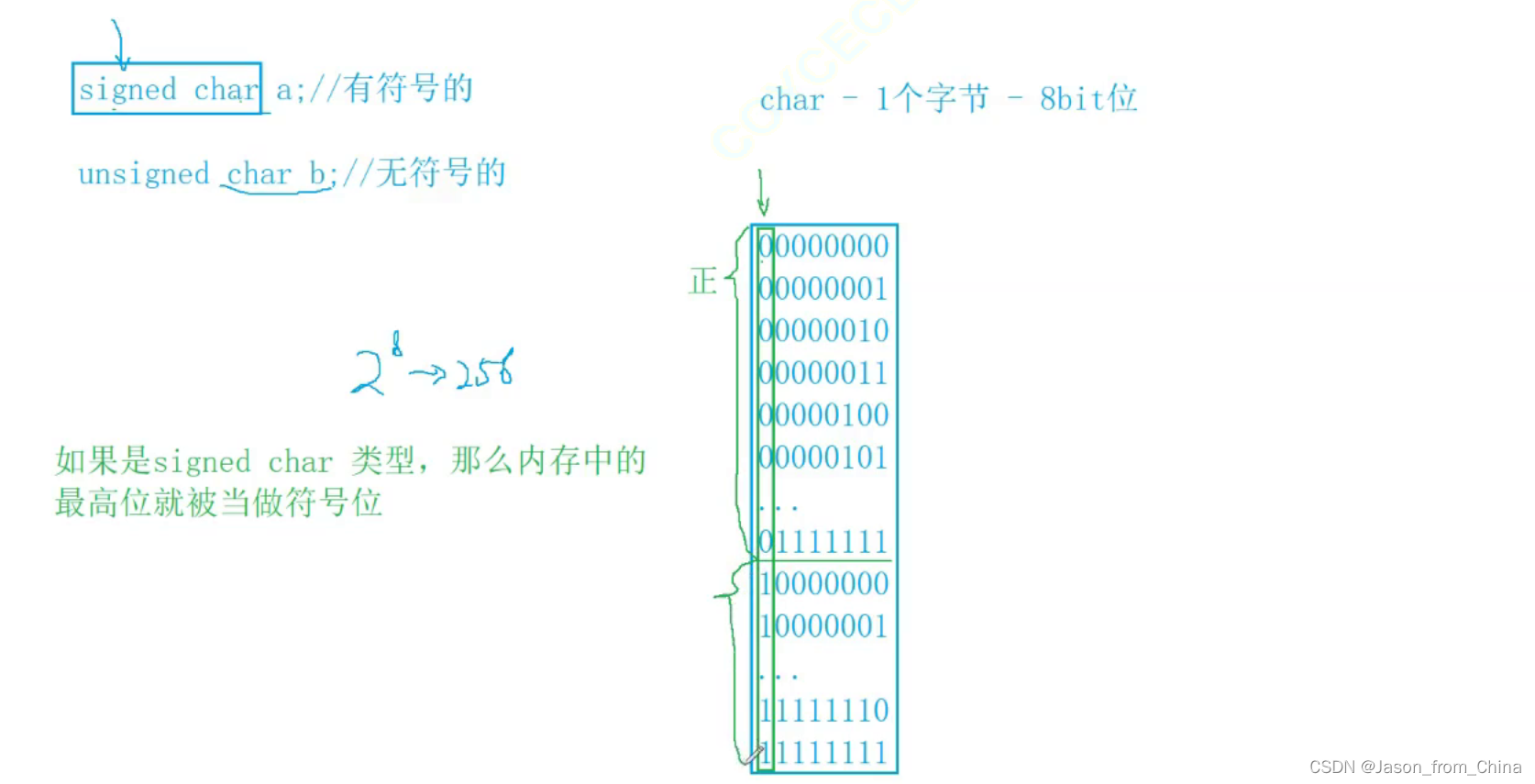

这里只能存放127 128放不下 所以 直接让10000000固定为-128
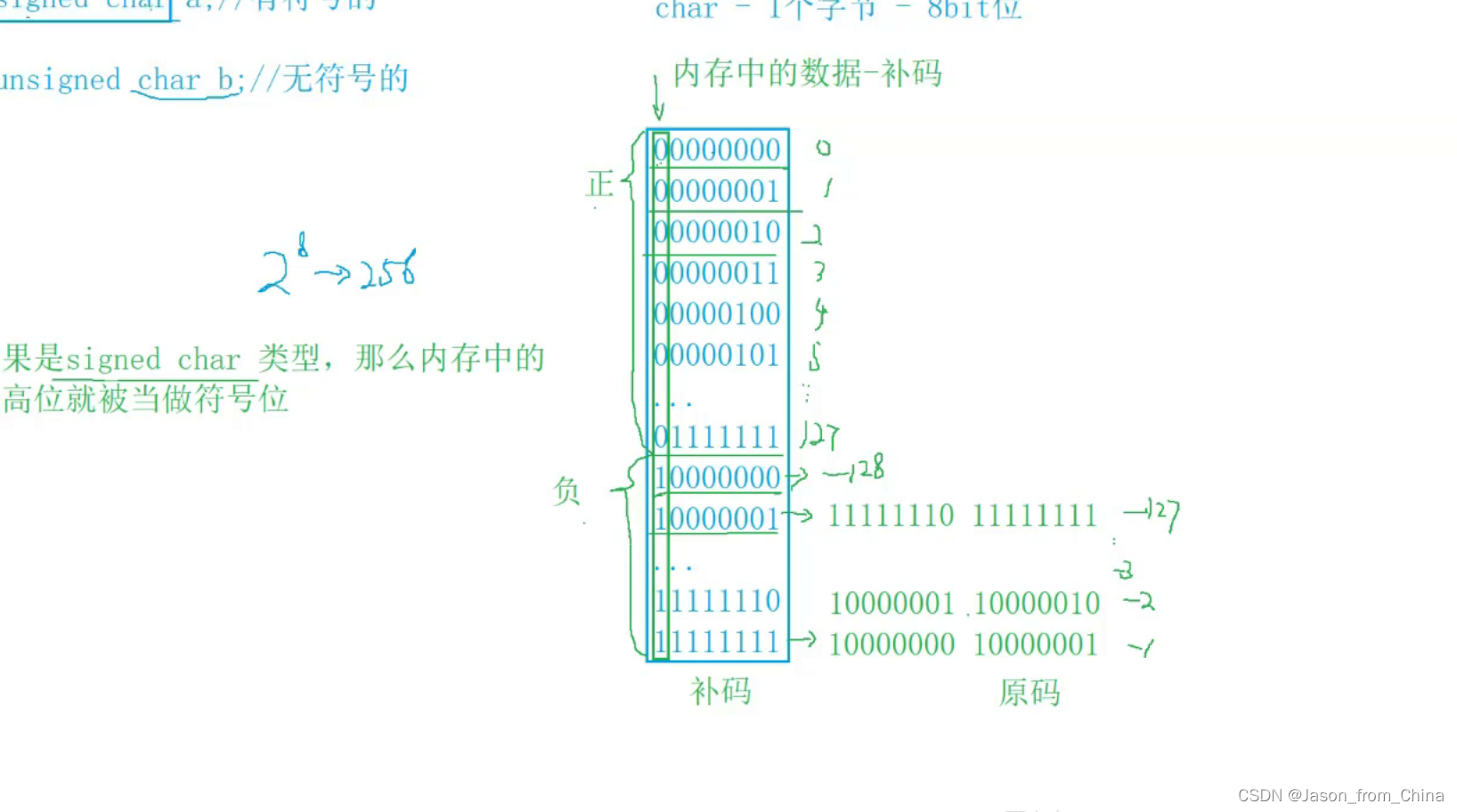
所以有符号整形的取值范围是取值是-128--127
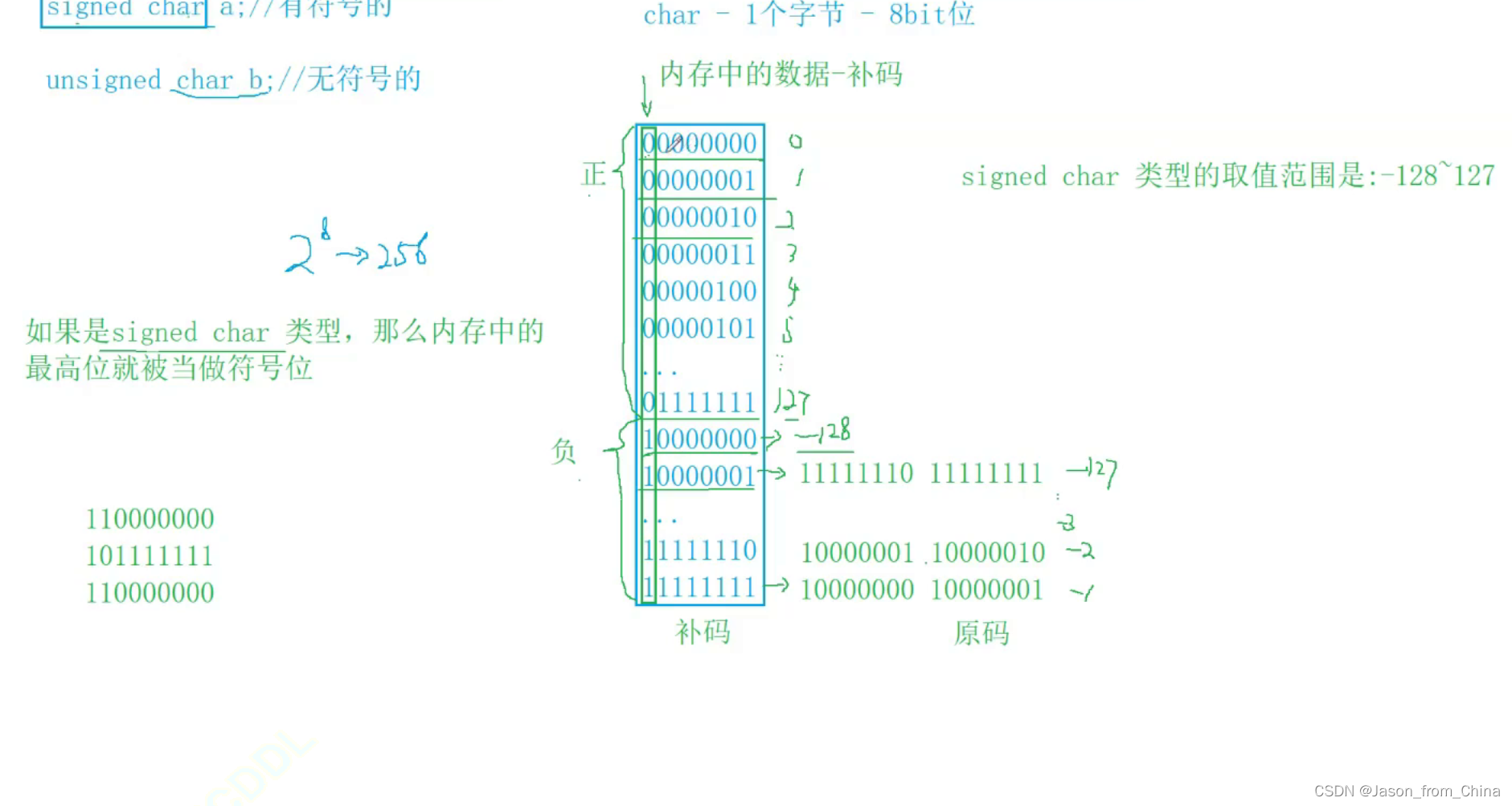
———————————————————————————————————————————
无符号整形的图解
无符号char类型举例
对于无符号 没有正负之分
所以这里的取值范围是0-255

整形提升的补充
1的补码是全11111111111111111111111111111111
整形打印不满足32位 要进行整形提升
———————————————————————————————————————————
大小端的练习3
代码
#include <stdio.h>
int main()
{
char a = -128;
printf("%u\n",a);
return 0;
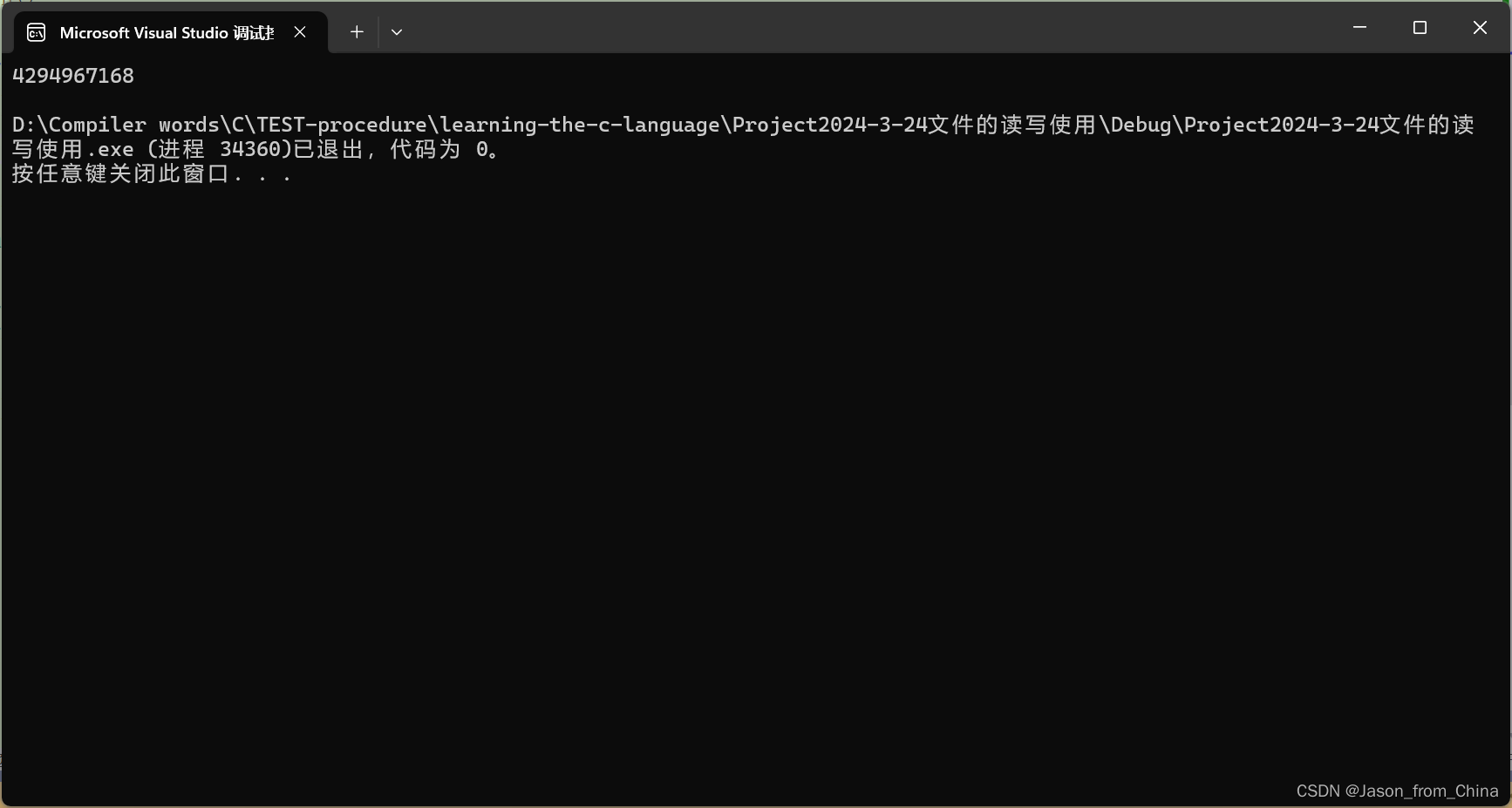
}代码解析
#include <stdio.h>
int main()
{
char a = -128;
//10000000 00000000 00000000 10000000补码
//11111111 11111111 11111111 01111111反码
//11111111 11111111 11111111 10000000补码
//10000000截断
//%u无符号打印 a是char类型 因为发生截断 所以先进行整形提升
//按照符号位进行整形提升 也就是
//11111111 11111111 11111111 10000000打印
//但是
//%u无符号打印
//所以 打印的时候 还是会不打印正负号
//所以结果他也就是 很大的数字 4294967168
//
printf("%u\n",a);
return 0;
}
———————————————————————————————————————————
大小端的练习4
#include <stdio.h>
int main()
{
char a = 128;
printf("%u\n",a);
return 0;
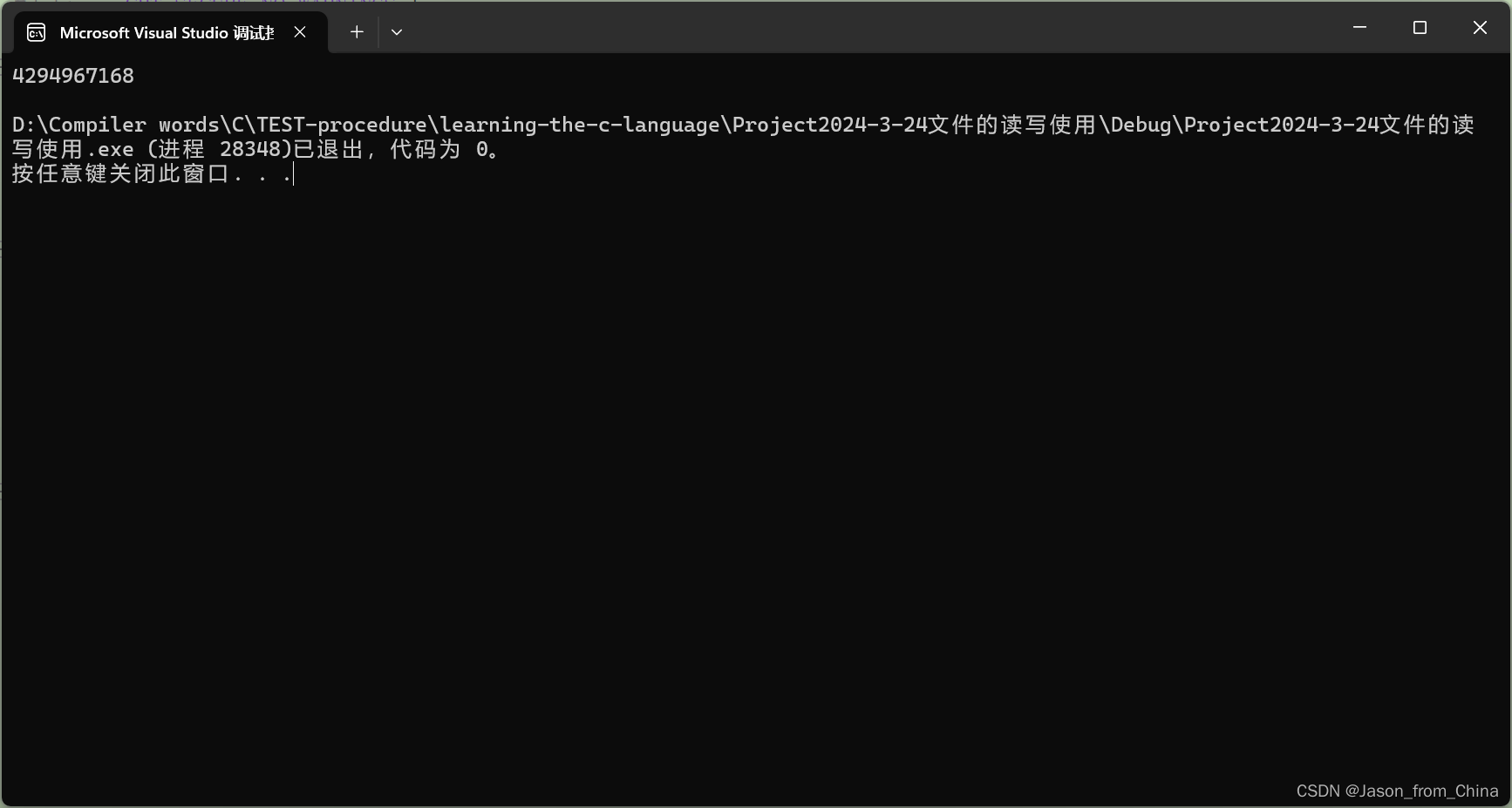
}代码解释
#include <stdio.h>
int main()
{
char a = 128;
//00000000 00000000 00000000 10000000补码
//00000000 00000000 00000000 10000000反码
//00000000 00000000 00000000 10000000补码
//10000000截断
//%u无符号打印 a是char类型 因为发生截断 所以先进行整形提升
//按照符号位进行整形提升 也就是
//11111111 11111111 11111111 10000000整形提升 按照符号位进行提升
//但是
//%u无符号打印
//所以 打印的时候 还是会不打印正负号
//所以结果他也就是 很大的数字 4294967168
//
printf("%u\n",a);
return 0;
}
———————————————————————————————————————————
大小端的练习5
#include <stdio.h>
int main()
{
char a[1000];
int i;
for(i=0; i<1000; i++)
{
a[i] = -1-i;
}
printf("%zd",strlen(a));
return 0;
}代码的讲解
首先我们需要知道这里是char类型 而且是有符号类型的
也就char类型占据一个比特位
他的最大值也就是11111111
他的最小值也就是00000000
所以 我们画个图可以理解为
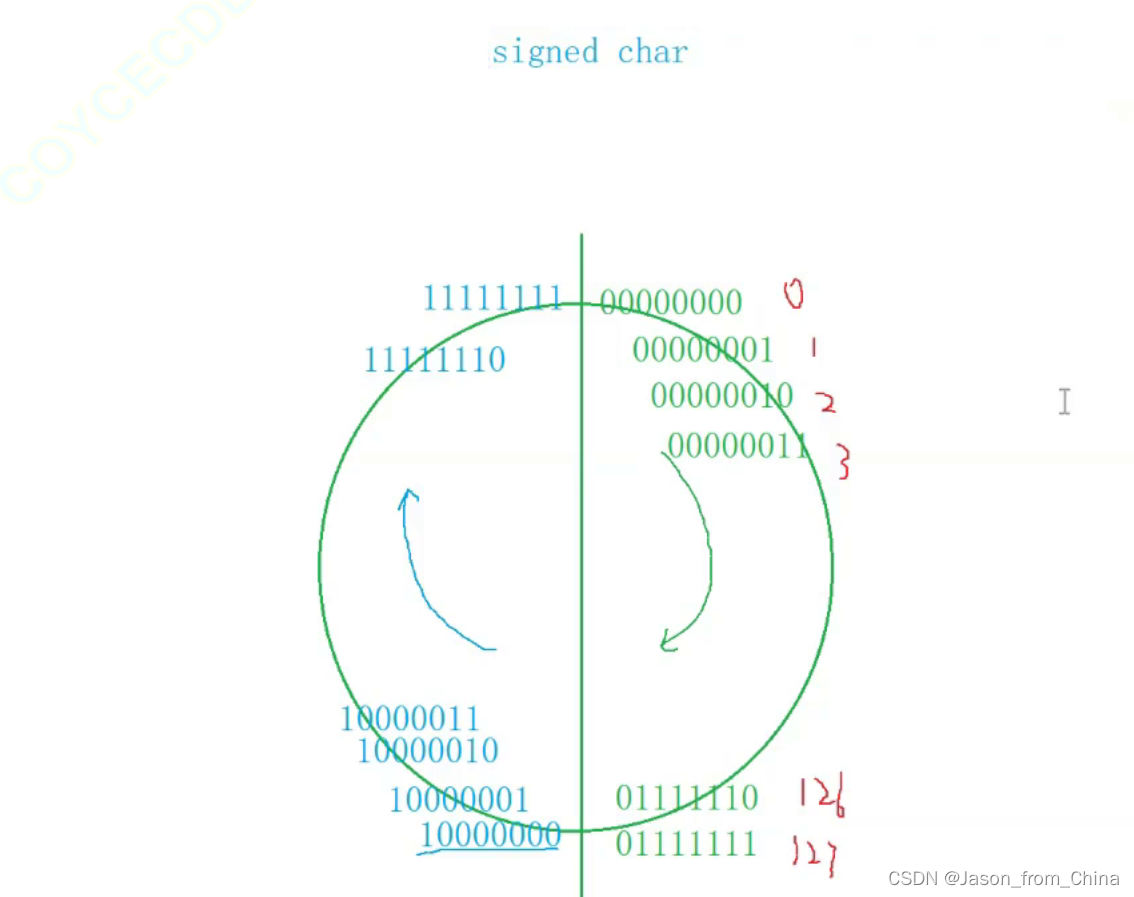
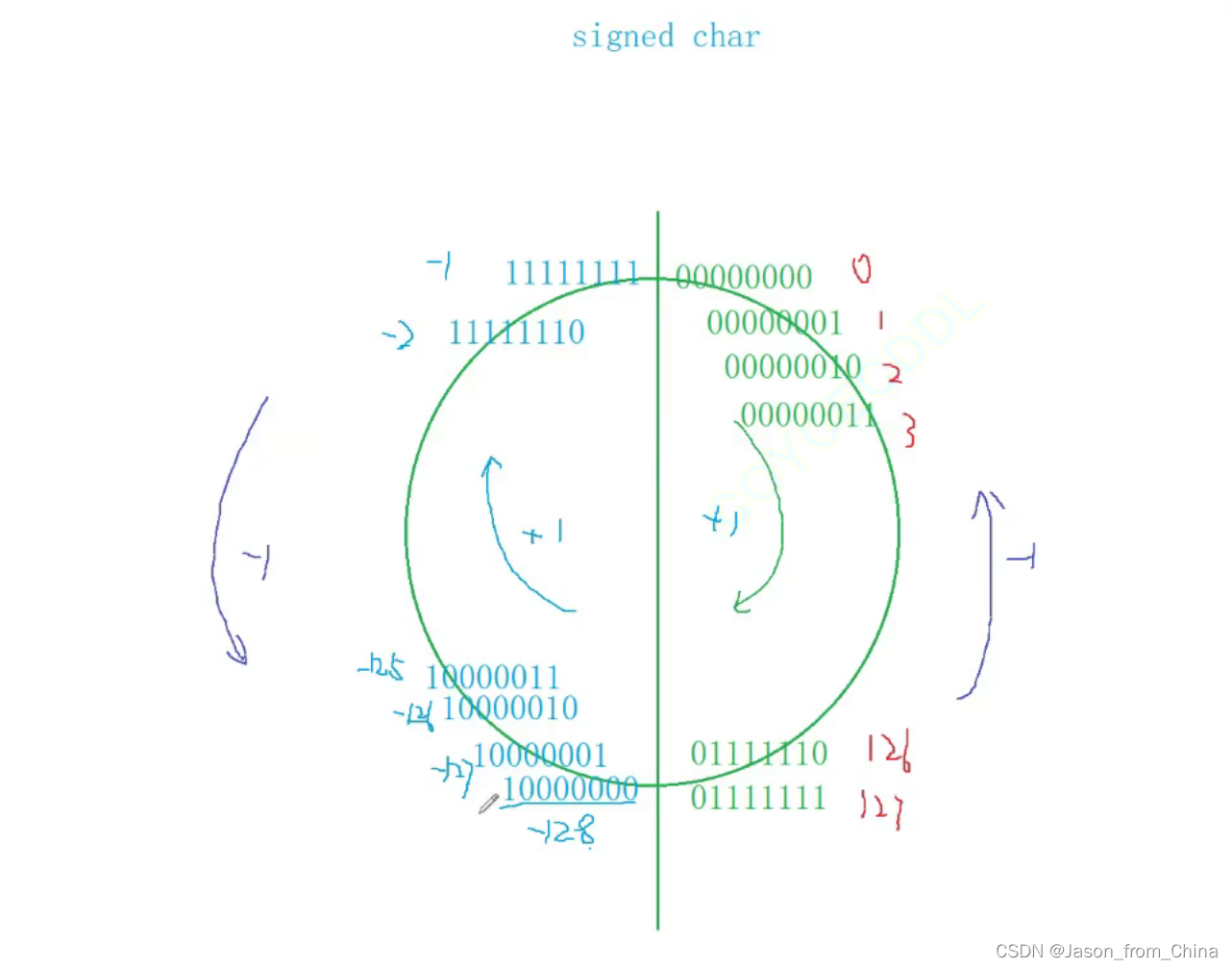
对于代码的图解

所以结果是255
同理我们也可以知道
既然我们可以推算出有符号char类型的最大值是-127~127
那么我们也可以推算出其他类型的大小
也就是说明,计算机里面 类型的大小是有边界的
不同的类型的大小是不一样的
char: 标准规定 char 类型至少为8位(1字节),可以是有符号或无符号的。
有符号 char 的取值范围是从 -128 到 127,
无符号 char 的取值范围是从 0 到 255。
11111111
10000000-01111111
short: 标准规定 short int 类型至少为16位(2字节),可以是有符号或无符号的。
有符号 short 的取值范围是从 -32768 到 32767,
无符号 short 的取值范围是从 0 到 65535。
11111111 11111111-0
10000000 00000000-01111111 1111111
int: 标准规定 int 类型至少为16位(2字节),但通常在32位系统上使用32位(4字节)。
有符号 int 的取值范围是从 -2147483648 到 2147483647,
符号 int 的取值范围是从 0 到 4294967295。
11111111 11111111 11111111 11111111-0
10000000 00000000 00000000 00000000-01111111 11111111 11111111 11111111
int: 标准规定 int 类型至少为16位(2字节),但通常在32位系统上使用32位(4字节)。有符号 int 的取值范围是从 -2147483648 到 2147483647,无符号 int 的取值范围是从 0 到 4294967295。但是要注意的是,32位系统上的 int 通常是这样表示的:
11111111 11111111 11111111 11111111 - 0
10000000 00000000 00000000 00000000 - 0代码的总结
#include <stdio.h>
int main()
{
char a[1000];
//首先我们知道 这里是char字节 也就是 01111111-10000000 这也就是取值区间
//但是我们需要知道的是 这里打印的方式是无符号打印的方式
//需要知道的是 就算是无符号整形打印 本质这里面还是按照-127~128进行计算的
//计算和打印是区分开的
int i;
for(i=0; i<1000; i++)
{
a[i] = -1-i;
//这里进行循环的计算 也就是-1,-2,-3,-4,-5.......-127,....128.....-2.进行循环 直到循环结束
}
//关键点在这里 这里strlen计算的是'\0'之前的字符的个数 这里也就是一直进行循环也就是 -127~128
//所以也就是255
printf("%zd",strlen(a));
//zd的打印整形
return 0;
}
———————————————————————————————————————————
大小端的练习6
#include <stdio.h>
unsigned char i = 0;
int main()
{
for(i = 0;i<=255;i++)
{
printf("hello world\n");
}
return 0;
}代码的解析
#include <stdio.h>
//首先 根据上面的讲解 我们知道 有符号整形的取值范围和无符号整形的取值范围
//很显然 这里是无符号整形 取值范围是0~255
unsigned char i = 0;
int main()
{
//接下来我们看这个循环 这个循环一直是小于地等于255的
//什么意思呢 也就是 这个循环条件一直满足 所以导致不停打印 导致死循环
for(i = 0;i<=255;i++)
{
printf("hello world\n");
}
return 0;
}
当数值等于255的时候还是小于等于255 继续开始新的循环
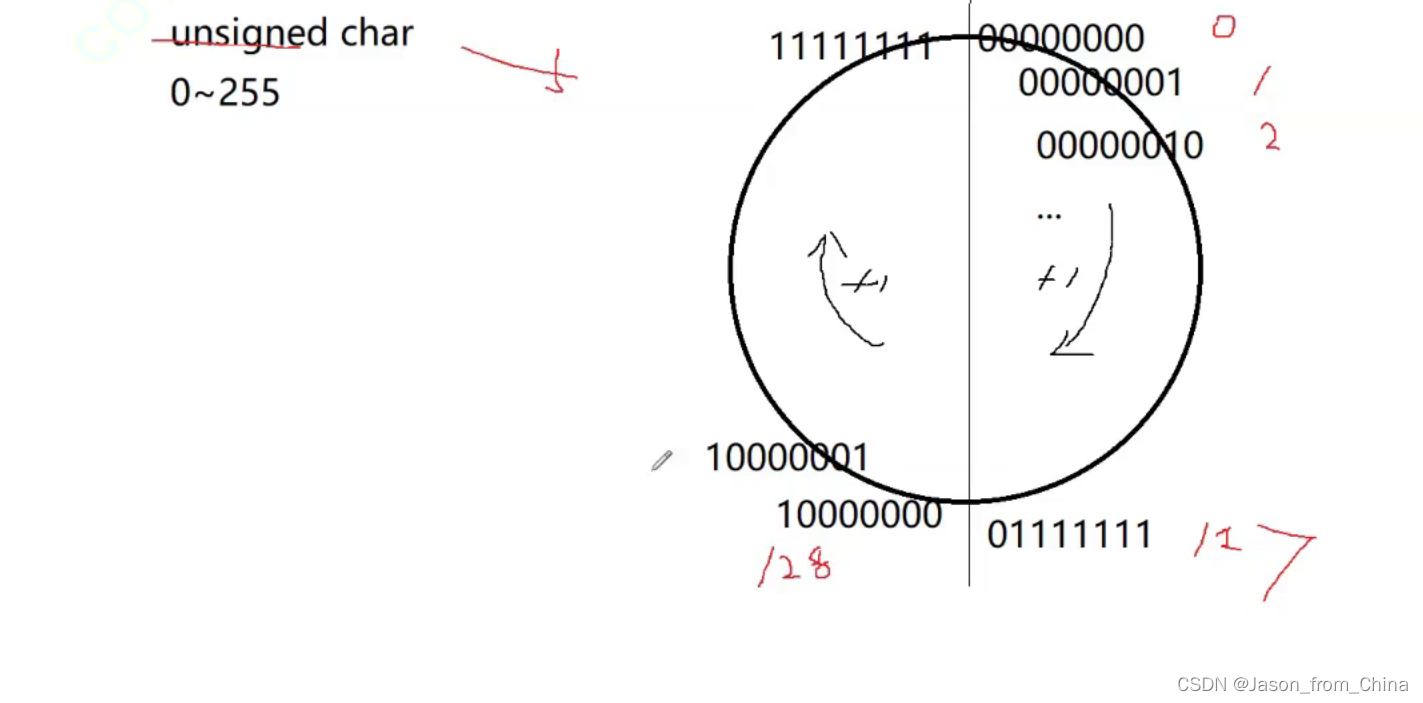
所以这个代码是死循环代码 是错误代码 
———————————————————————————————————————————
大小端的练习7
#include <stdio.h>
int main()
{
unsigned int i;
for(i = 9; i >= 0; i--)
{
printf("%u\n",i);
}
return 0;
}
代码的解析
#include <stdio.h>
int main()
{
unsigned int i;
//首先 这里是无符号整形
//所以计算的范围是大于0 的
//加下来我们看看循环条件
//这个循环条件是 只要大于0 就会一直进行 循环 所以一直满足条件 导致死循环
for(i = 9; i >= 0; i--)
{
printf("%u\n",i);
}
return 0;
}
同理也是死循环
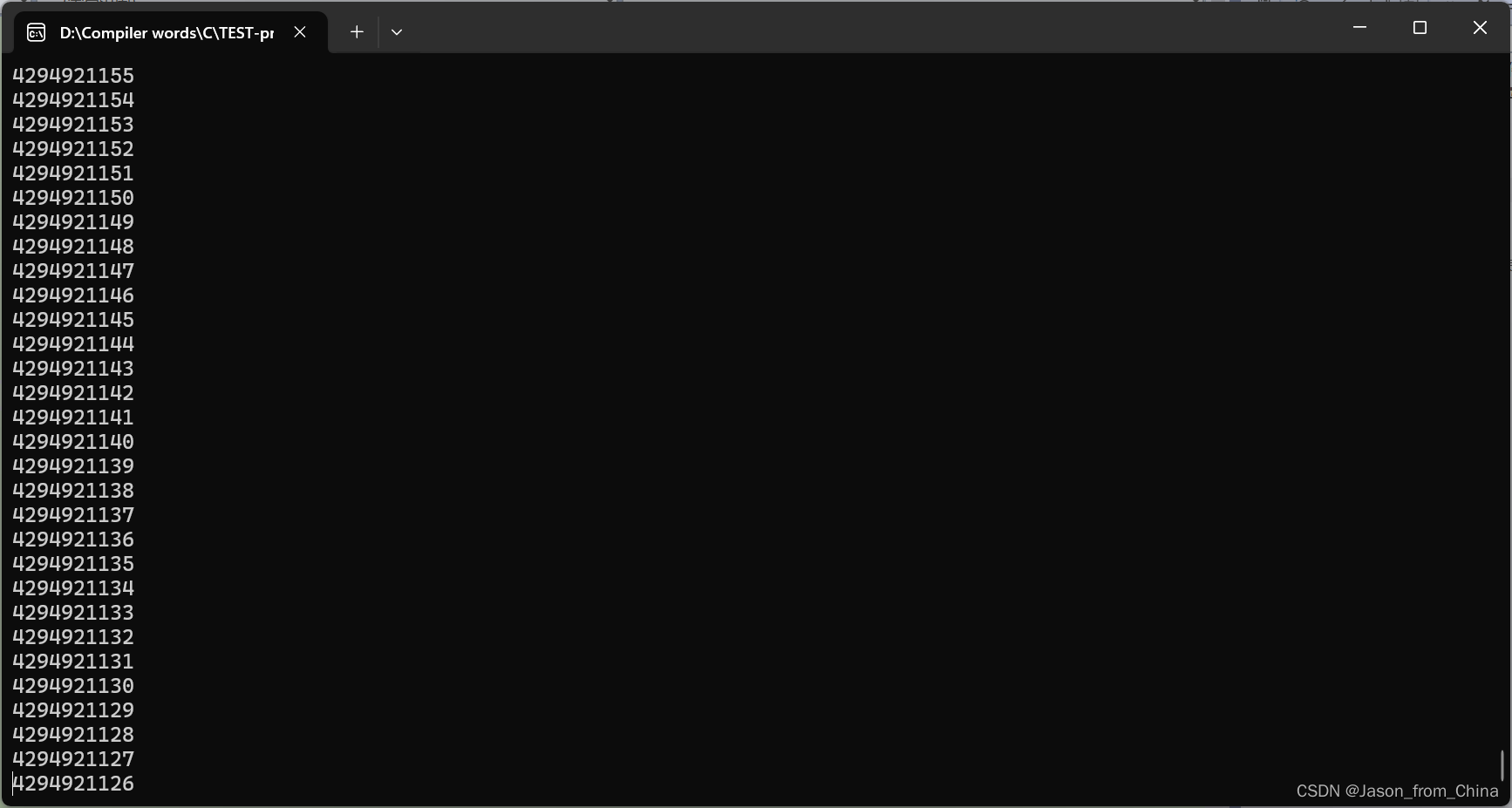
———————————————————————————————————————————
大小端的练习8
#include <stdio.h>
int main()
{
int a[4] = { 1, 2, 3, 4 };
int *ptr1 = (int *)(&a + 1);
int *ptr2 = (int *)((int)a + 1);
printf("%x,%x", ptr1[-1], *ptr2);
return 0;
}
图解
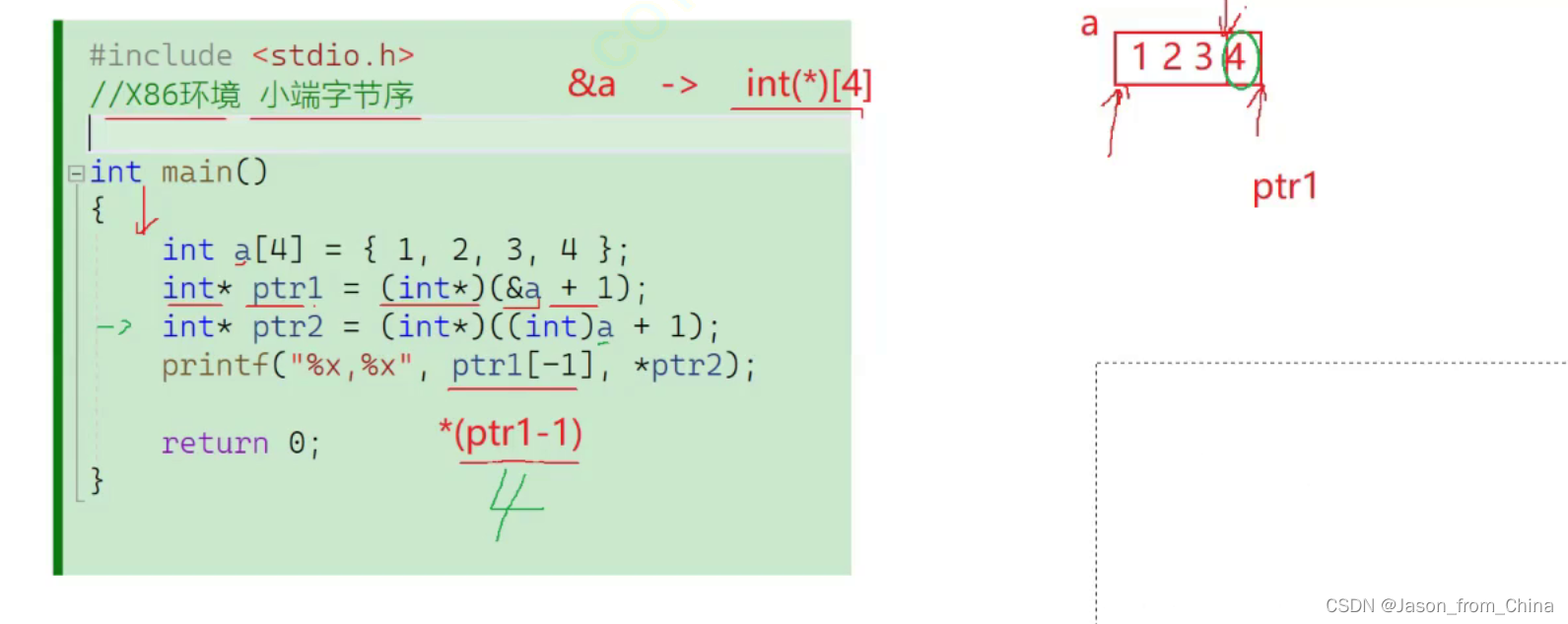
指针+1 是取决于整形类型
整形+1 就是+1
这里是强制类型转化为整形也就是+1
再次强制转化为int* 四个字节也就是此时变成这样

所以指向的是这四个字节

这四个字节按照小端内存的方式存储
低位放在低地址,高位放在高地址

所以结果就是 0x4,0x2000000

代码的解析
#include <stdio.h>
int main()
{
//这里是一个整形数组 1 2 3 4
int a[4] = { 1, 2, 3, 4 };
//这里是一个指针首先是取地址 整个数组的地址 +1 并且强制转化为整形指针 所以指向的是最后一个地址+1
int *ptr1 = (int *)(&a + 1);
//这里是整形进行+1 并且强制转化为整形指针 也就是指向的是2
//指针+1 是取决于整形类型
//整形+1 就是+1
int *ptr2 = (int *)((int)a + 1);
//这里第一个 ptr1[-1]等价于*(ptr-1) 所以指向的从 最后一个地址+1 变成最后一个地址 也就是4
//第二个打印的是2 上面已经解释
printf("%x,%x", ptr1[-1], *ptr2);
return 0;
}
所以结果是
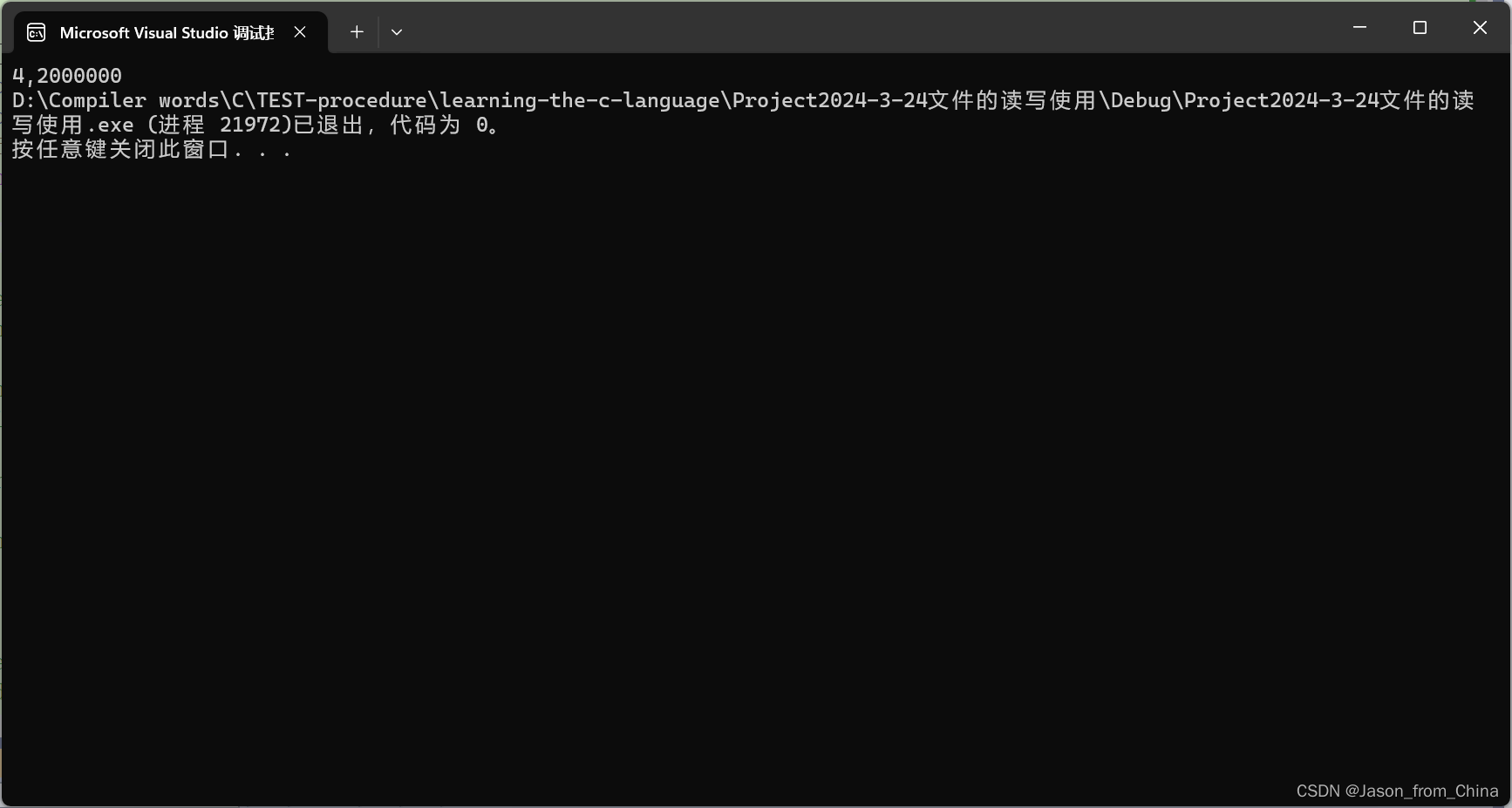
————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————
浮点数在内存中的存储
浮点数存储方式
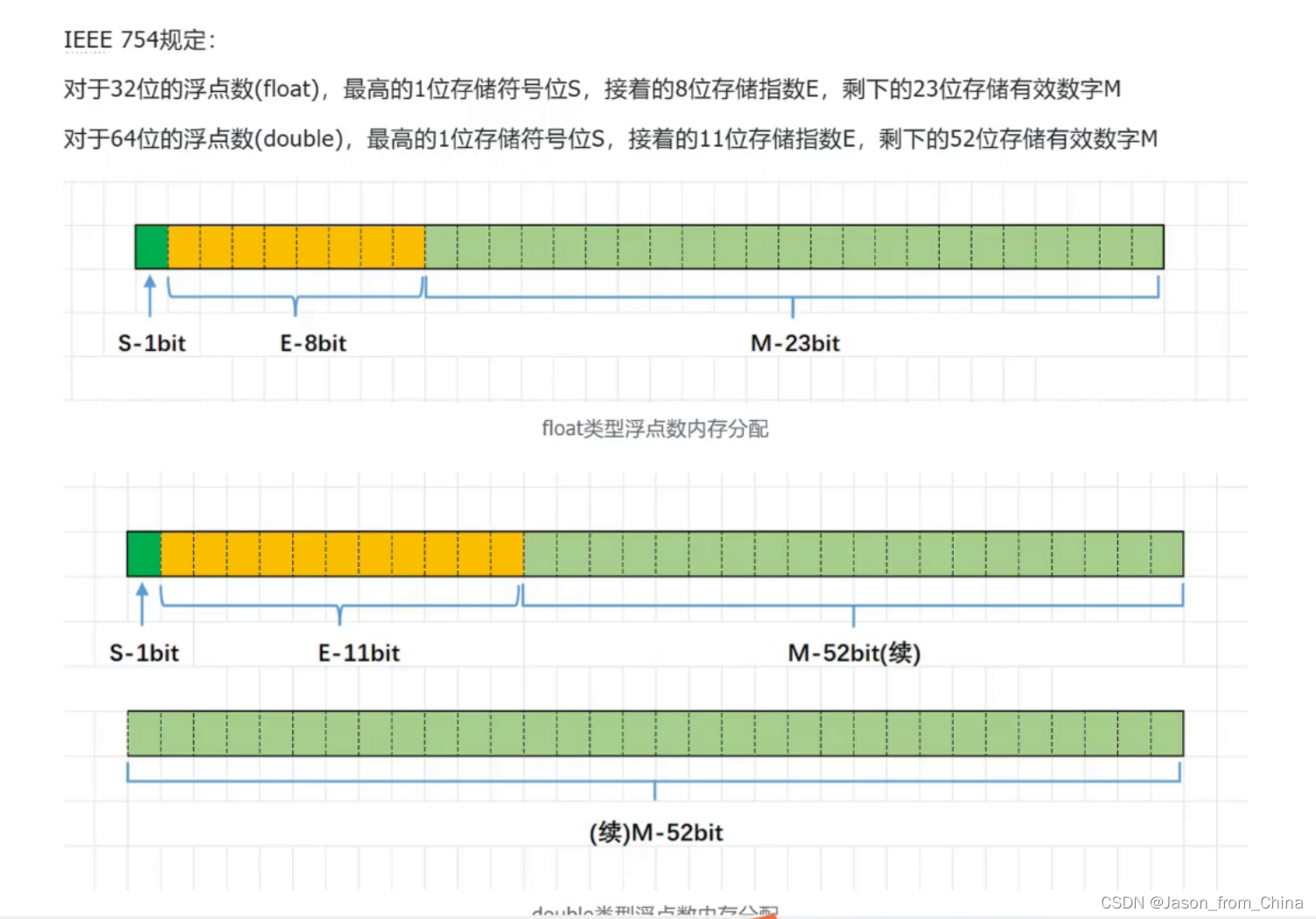
浮点数在内存中的存储方式遵循IEEE 754标准,通常分为32位和64位两种。
存储格式为V = (-1)^s * M * 2^E,
其中s是符号位,M表示有效数字,E表示指数[2]。对于32位浮点数,其存储结构为:
最高位为符号位,接着8位为指数位,剩余的23位为有效数字。实际可保存的有效数字位为24位[10]。
对于64位浮点数,最高位也是符号位,接着11位为指数位,剩余的52位为有效数字,实际可保存的有效数字位为53位[10]。
在存储时,有效数字M的小数部分可以节省1位,读取时再补上[5][10]。
指数E为无符号整数,对于8位E,其取值范围为0-255;对于11位E,其取值范围为0-2047[10]。
实际存储时,E的真实值需加上一个中间值。32位浮点数的E中间值为127,64位浮点数的E中间值为1023[10]。
浮点数在内存中的取过程分为三种情况:
1. E不全为0或1,此时浮点数表示需按照指数E的计算值减去127(或1023),再加上有效数字M。
2. E全为0,表示真实值,有效数字M不再加1。
3. E全为1,表示±无穷大[10]。
需要注意的是,不同的编译器或硬件平台可能采用不同的字节序,即“大端字节序”或“小端字节序”。大端字节序存储是将高位数据存储在低地址处,低位数据存储在高地址处;小端字节序存储则是将高位数据存储在高地址处,低位数据存储在低地址处[5][9]。
———————————————————————————————————————————
浮点数代码对比和整数的区别
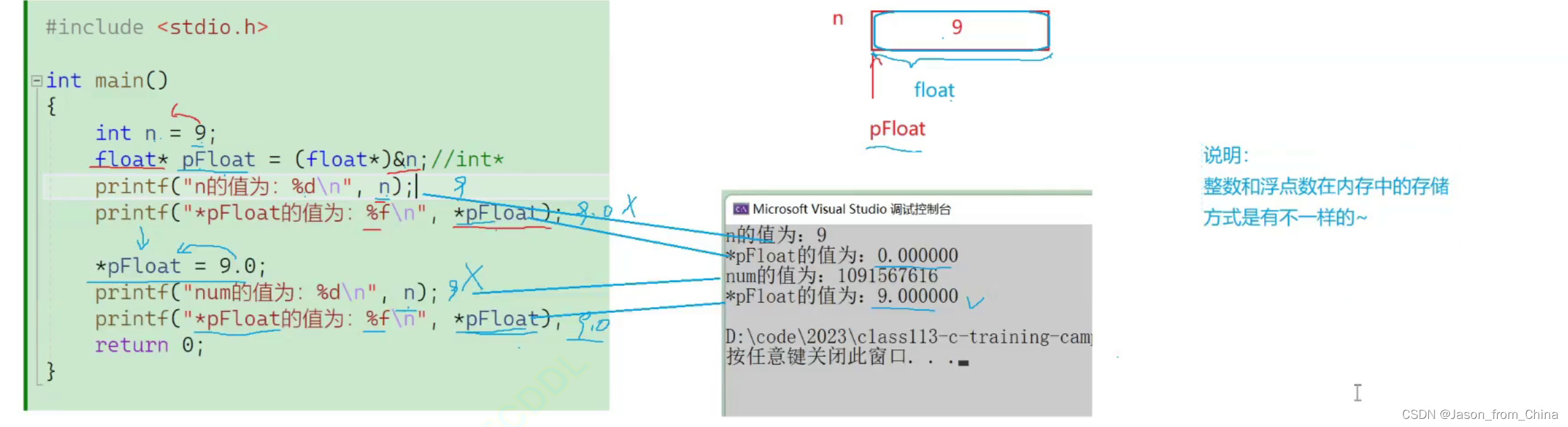
这里首先上一个代码 进行和整数的对比
主要负责说明浮点数和整数在内存里面的存储方式是不一样的

从这个代码的转换里面 我们可以了解到
整数和浮点数在内存里面的存储方式是不一样 的
n是整数,放进去 拿出来的数值是不一样的
举个我之前老师讲的例子来说 在西风国家亲个嘴没啥 但是在中国古代没结婚 亲个嘴不得了了
———————————————————————————————————————————
浮点数的储存规则
首先 我们可以看到 浮点数的存储的规则是有公式的 我们根据公式,套图片很容易理解

——————————————————————————————————————————
小数点如何换算成二进制

小数点向左移动两位 所以是2次方
下面的2 是几进制
这个小数点换算成而二进制可以理解为
1 可以理解为
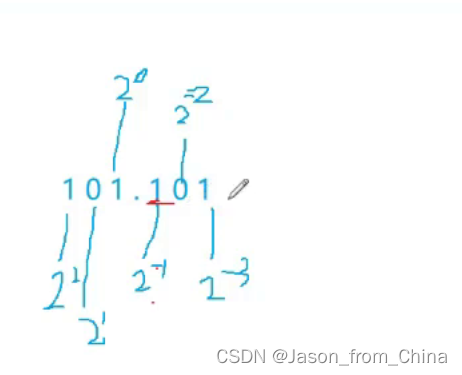
2 也可以理解为
小数点后面的数字换算成二进制,实际上就是将这个小数转换成二进制分数。以0.625为例,我们将其转换成分数,即625/1000。接下来,我们将这个分数转换成二进制。
首先,我们将分子625和分母1000同时除以2,得到312.5和500。我们将312.5作为新的分子,500作为新的分母,重复除以2的过程。
```
625 ÷ 1000 = 0.625
312.5 ÷ 500 = 0.625
```
由于312.5除以500的结果仍然是0.625,我们可以知道,这个分数可以一直除以2下去,而且商永远都是0.625。因此,0.625的二进制表示就是0.101。
其他小数点后的数字换算成二进制的方式也是类似的,关键在于将小数转换成分数,然后不断地将分子和分母除以2,直到分子不再改变为止。——————————————————————————————————————————
浮点数公式的计算讲解
关于E
小数点向左移动两位 所以是2次方
但是放在内存里面需要+127 下面我们会详细解释 不要着急
关于S
s可以为1或者0 因为这里是判断正负值
如果是正数 那么s数值就是0
如果是负数 那么s的数值就是-1
关于M
1.011是M
这个数值是怎么来的
可以这样理解 经过计算,计算出5.5的二进制是101.1
101.1->可以计算成1.011*10平方
但是这里是二进制的计算 所以是
101.1->1.01*10^2
由此得出,M的数值是1.011
同时得出s的数值是2 也就是2次方
图解

——————————————————————————————————————————
浮点数内存的划分使用
我们可以看见 在计算机的存储里面
上面的是32位环境,内存划分的使用
下面的是64位环境,内存划分的使用
清晰的标注出SEM在内存的划分方式
——————————————————————————————————————————
浮点数存储的过程
浮点数在计算机中的存储是通过遵循一定的标准和规范来实现的,其中最常见的是IEEE 754标准。
下面是浮点数在计算机中存储的一般过程:
1. **标准化表示**:为了能够在计算机中统一存储和处理浮点数,首先要对浮点数的表示方法进行标准化。这包括确定数的表示范围和精度。在IEEE 754标准中,浮点数被分为单精度(32位)和双精度(64位)两种,还有其他较少用的类型。
2. **表示格式**:浮点数通常分为三部分:符号位、指数和尾数。
- **符号位**:表示数的正负,通常是一个单独的位。
- **指数**:表示数的规模或大小,通常采用偏移量(如+127)的编码方式,以允许表示正负指数。
- **尾数**:表示数的实际精度,是浮点数的主要部分,通常是一个二进制小数。
3. **二进制表示**:将浮点数的实际值转换为二进制形式。这包括将数的整数部分和小数部分分别转换为二进制,并合并成一个连续的二进制数。
4. **规格化**:为了便于存储和处理,浮点数通常要进行规格化处理。规格化的目的是将尾数的最高位设置为1,这样可以简化浮点数的运算算法,并确保所有的浮点数都在一个固定范围内。
5. **编码**:将规格化后的二进制数按照浮点数的表示格式进行编码,形成最终的存储形式。在IEEE 754标准中,这个过程还包括将符号位、指数和尾数的二进制编码插入到固定位置。
6. **存储**:最后,将编码后的浮点数按照计算机的字长(如32位或64位)存储在内存中。
在计算机内部进行浮点运算时,首先要对存储的浮点数进行解码,然后进行相应的数学运算,最后将结果重新规格化并编码存储。
这个过程体现了计算机在处理浮点数时的高效性和统一性,使得不同计算机系统和编程语言能够在浮点数的表示和处理上实现兼容和通用。

5.5的二进制 101.1
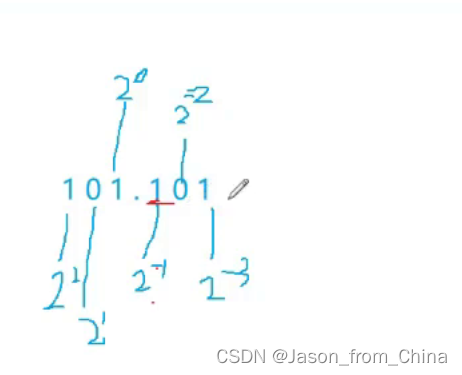
这里得到指数E之后 需要知道 指数的计算放到内存里面
需要+127 拿出来的时候需要-127
——————————————————————————————————————————
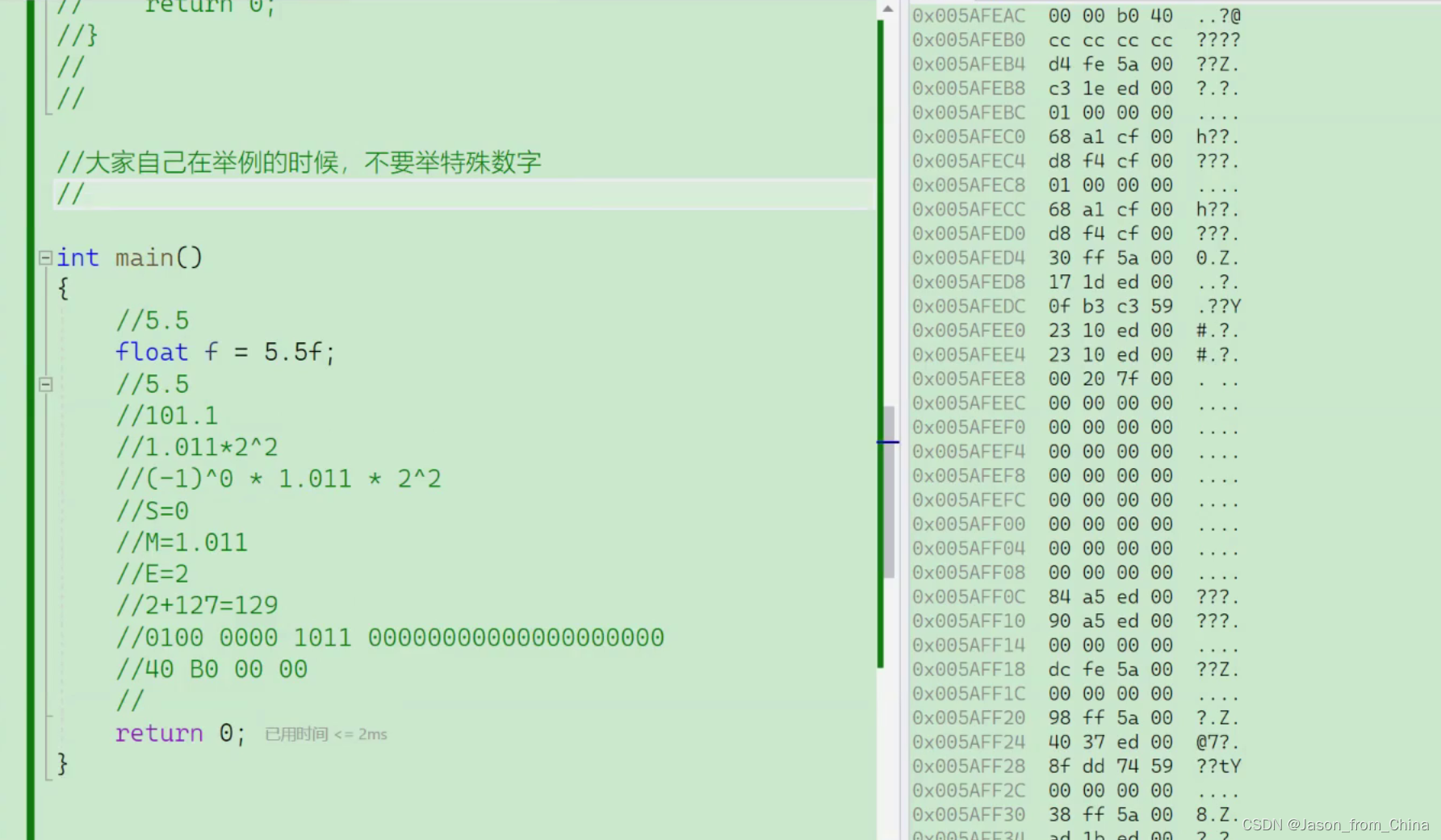
这里拿一个代码进行举例(计算的详细解剖)重点

这里我们找的是32位的环境 
计算机的划分是1bit位(S)+8bit位(E)+23bit位(M)
这里是拿5.5在计算机里面的存储来进行举例
1. 首先判断出这个是正数所以是0->S,得出0的二进制是0
2. 5.5换算成二进制也就是101.1—>M
3. E也就是次方倍数,M变成1.011,得出1.011*2^2所以得出2—>E,1.011->M
这个时候我们得出M的二进制也就是011,为什么是011,因为计算机计算原理里面规定可以省略,因为我们已知指数幂,已知正负数,1.011我们可以把前面的省去,计算机根据指数幂可以推算出次方是正数还是负数,得出SME ,所以计算的时候自动把小数点前的省去。方便存储和计算。
4. 根据换算我们可以知道 指数是需要加127的 因为小数的二进制是可能是负数的也就是,如果 是0.123等等,这都是负数的,所以需要+127,所以得出E的存储的数值是2+127=129
得出129的二进制是10000001
5. 也就是最后一步,也就是根据内存的划分和使用
也就是
0(S) 10000001(E) 011(M)
但是计算机的计算里面,计算的时候是需要满足32位的所以需要补满32位,所以我们补满0 就可以了
0 10000001 01100000000000000000000
——————————————————————————————————————————
举例的二次解析
所以此时我们也就清除了 为什么在代码里面进行整数和浮点数的换算得到的结果是不一样的
因为换算的逻辑是不一样的