回归问题 vs 分类问题(regression vs classification)
回归问题(regression)
1、回归问题的目标是使预测值等于真实值,即pred=y。
2、求解回归问题的方法是使预测值和真实值的误差最小,即minimize dist(pred,y),一般我们通过求其2-范数,再平方得到它的最小值,也可以直接使用1-范数。
分类问题(classification)
1、分类问题的目标是找到最大的概率,即maximize benchmark(accurcy)。
2、求解分类问题,第一种方法是找到真实值与预测值之间的最小距离,即minimize dist( p(y | x), pr(y | x) )。第二种方法是找到真实值与预测值的最小差异,即minimize divergence( p
(y | x), pr(y | x) )
但是,为什么不直接就概率呢?
1、如果概率不发生改变,权重发生改变,就会导致梯度等于0,出现梯度离散的现象。
2、由于正确的数量是不连续的,因此造成梯度也是不连续的,会导致梯度爆炸、训练不稳定等问题。
二分类问题(Binary Classification)
给定一个函数 f :x ---> p(y = 1 | x),如果二分类的角度去研究这个问题。预测的方法是:如果p(y = 1 | x) > 0.5 ,则预测值为1,否则预测值为0。
以交叉熵的角度分析二分类问题:
首先将二分类问题实例化,是对于猫和狗的分类问题,根据概率之和等于1,我们可以得到狗的概率等于1减去猫的概率,即P(dog) = (1 - P(cat)),接着将其带入到交叉熵公式中,得到以下公式:
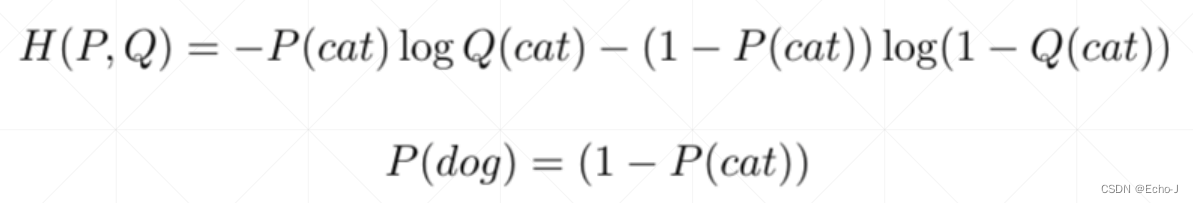
将具体问题扩展到 一般问题,得到如下公式:

分析以上公式,当y = 1 时,H (P, Q) = log(p);当y = 0 时,H (P, Q) = log(1 - p);这两种情况随着p的变化,单调性是相反的,进一步证明了交叉熵解决二分类问题的可行性。
多分类问题(Multi-class classification)
给定一个函数 f :x ---> p(y | x) ,其中 [𝑝 𝑦 = 0 𝑥 , 𝑝 𝑦 = 1 𝑥 , … , 𝑝 𝑦 = 9 𝑥 。必须满足:所有的𝑝 (𝑦 |𝑥) ∈ [0, 1];所有的概率和 𝑝 (𝑦 = 𝑖 |𝑥 )= 1。
如何让所有的概率和为1呢?
使用softmax函数,详情请看深度学习pytorch——激活函数&损失函数(持续更新)-CSDN博客
交叉熵(cross entropy)
1、交叉熵的特点:
(1)具有很高的不确定性
(2)度量很惊喜
2、交叉熵的公式:

3、交叉熵的值越高就代表不稳定性越大
(1)以代码的方式解释
可以清楚的观察到数据的分布越平衡,最后得到的熵值就越高,反之,熵值就越低。
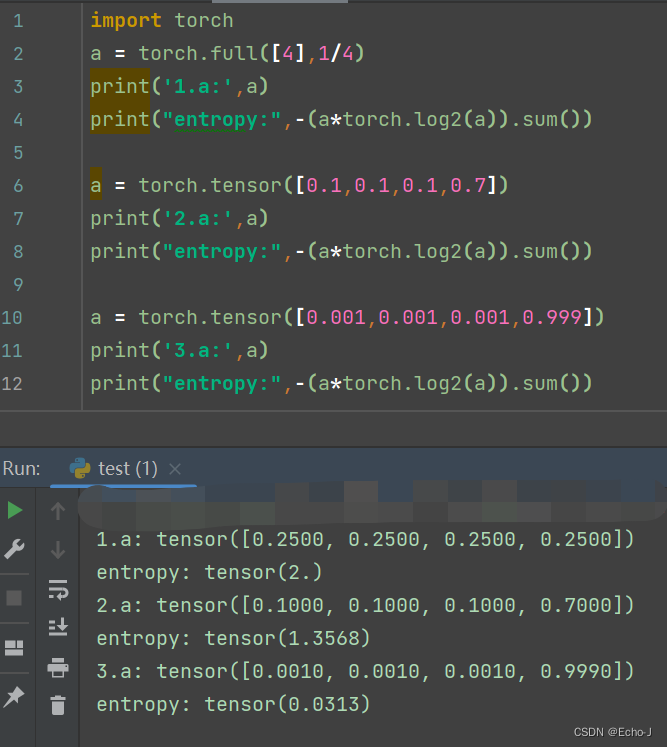
import torch
a = torch.full([4],1/4)
print('1.a:',a)
print("entropy:",-(a*torch.log2(a)).sum())
a = torch.tensor([0.1,0.1,0.1,0.7])
print('2.a:',a)
print("entropy:",-(a*torch.log2(a)).sum())
a = torch.tensor([0.001,0.001,0.001,0.999])
print('3.a:',a)
print("entropy:",-(a*torch.log2(a)).sum())(2)以理论的角度解释
给出Cross Entropy 的公式:

当Cross Entropy 和Entropy 这两个分布相等时,即H(p,q)=H(p),此时两个分布重合,此时Dkl就等于0。
当使用one-hot加密,我们可以得到Entropy = 1log1 = 0,即H(p)= 0,则此时满足H(p, q) = Dkl(p|q)的情况,此时如果对H(p,q)进行优化,相当于将Dkl(p|q)直接优化了,这是我们直接可以不断减小Dkl(p|q)的值,使预测值逐渐接近真实值,这就很好的解释了我们为什么要使用Cross Entropy。
为什么不使用MSE?
1、sigmoid + MSE 的模式会导致梯度离散的现象
2、收敛速度比较慢
通过下图可以很合理的证明以上两个原因的合理性:
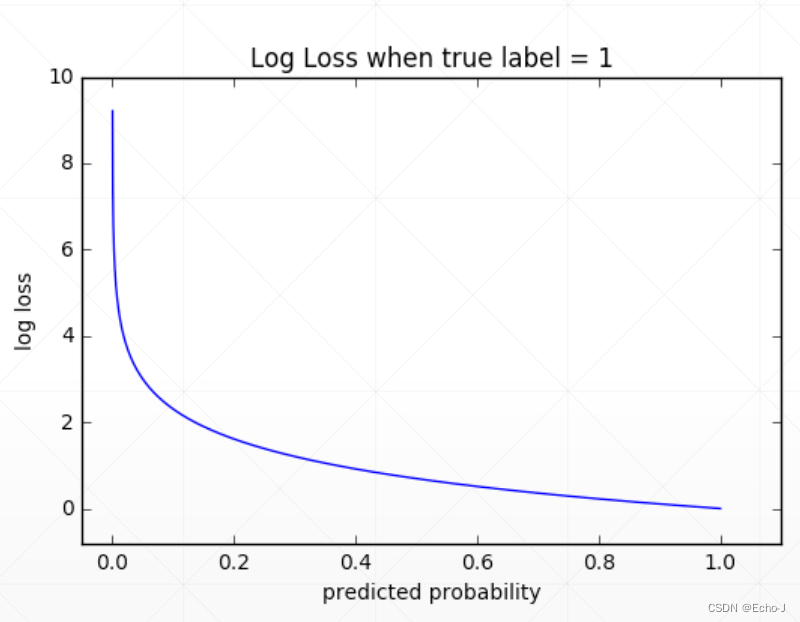
3、但是有时我们再做一些前沿的技术时,会发现MSE效果要好于cross entropy,因为它的求解梯度较为简单。
MSE VS Cross Entropy
Cross Entropy = sofymax + log + nll_loss,最后的结果都是一样的。
import torch
from torch.nn import functional as F
# MSE vs Cross Entropy
x = torch.randn(1,784)
w = torch.randn(10,784)
logists = x@w.t()
# 使用Cross Entropy
print(F.cross_entropy(logists,torch.tensor([3])))
# tensor(0.0194)
# 自己处理
pred = F.softmax(logists, dim = 1)
pred_log = torch.log(pred)
print(F.nll_loss(pred_log,torch.tensor([3])))
# tensor(0.0194)多分类问题实战
############# Logistic Regression 多分类实战(MNIST)###########
# (1)加载数据
# (2)定义网络
# (3)凯明初始化
# (4)training:实例化一个网络对象,构建优化器,迭代,定义loss,输出
# (5)testing
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
batch_size=200 #Batch Size:一次训练所选取的样本数
learning_rate=0.01
epochs=10 #1个epoch表示过了1遍训练集中的所有样本,这里可以设置为 5
# 加载数据
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
# 在pytorch中的定义(a,b)a是ch-out输出,b是ch-in输入,也就是(输出,输入)
# 比如第一个可以理解为从784降维成200的层
w1, b1 = torch.randn(200, 784, requires_grad=True),\
torch.zeros(200, requires_grad=True)
w2, b2 = torch.randn(200, 200, requires_grad=True),\
torch.zeros(200, requires_grad=True)
w3, b3 = torch.randn(10, 200, requires_grad=True),\
torch.zeros(10, requires_grad=True)
# 凯明初始化,如果不进行初始化会出现梯度离散的现象
# torch.nn.init.kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')
torch.nn.init.kaiming_normal_(w1)
torch.nn.init.kaiming_normal_(w2)
torch.nn.init.kaiming_normal_(w3)
# 前向传播过程
def forward(x):
x = x@w1.t() + b1
x = F.relu(x)
x = x@w2.t() + b2
x = F.relu(x)
x = x@w3.t() + b3
x = F.relu(x) #这里千万不要用softmax,因为之后的crossEntropyLoss中自带了。这里可以用relu,也可以不用。
return x #返回的是一个logits(即没有经过sigmoid或者softmax的层)
# 优化器
optimizer = optim.SGD([w1, b1, w2, b2, w3, b3], lr=learning_rate)
criteon = nn.CrossEntropyLoss()
for epoch in range(epochs):
for batch_idx, (data, target) in enumerate(train_loader):
data = data.view(-1, 28*28) # 将二维的图片数据打平 [200,784],第5课用的 x = x.view(x.size(0), 28*28)
logits = forward(data) #这里是网络的输出
loss = criteon(logits, target) # 调用cross—entorpy计算输出值和真实值之间的loss
optimizer.zero_grad()
loss.backward()
# print(w1.grad.norm(), w2.grad.norm())
optimizer.step()
# 每 batch_idx * 100=20000输出结果 每100个bachsize打印输出的结果,看看loss的情况
if batch_idx % 100 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
# len(data)---指的是一个batch_size;
# len(train_loader.dataset)----指的是train_loader这个数据集中总共有多少张图片(数据)
# len(train_loader)---- len(train_loader.dataset)/len(data)---就是这个train_loader要加载多少次batch
# 测试网络---test----每训练完一个epoch检测一下测试结果
# 因为每一个epoch已经优化了batch次参数,得到的参数信息还是OK的
test_loss = 0
correct = 0
for data, target in test_loader:
data = data.view(-1, 28 * 28)
logits = forward(data) #logits的shape=[200,10],--200是batchsize,10是最后输出结果的10分类
test_loss += criteon(logits, target).item() #每次将test_loss进行累加 #target=[200,1]---每个类只有一个正确结果
pred = logits.data.max(1)[1]
# 这里losgits.data是一个二维数组;其dim=1;max()---返回的是每行的最大值和最大值对应的索引
# max(1)----是指每行取最大值;max(1)[1]---取每行最大值对应的索引号
# 也可以写成 pred=logits.argmax(dim=1)
correct += pred.eq(target.data).sum()
#预测值和目标值相等个数进行求和--在for中,将这个test_loader中相等的个数都求出来
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
"""
影响training的因素有:
1、learning rate过大
2、gradient vanish---梯度弥散(参数梯度为0,导致loss保持为常数,loss长时间得不到更新)
3、初始化问题----参数初始化问题
"""课时50 多分类问题实战_哔哩哔哩_bilibili