Qt creator构建DLL库
news2026/2/12 16:35:55
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1540451.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
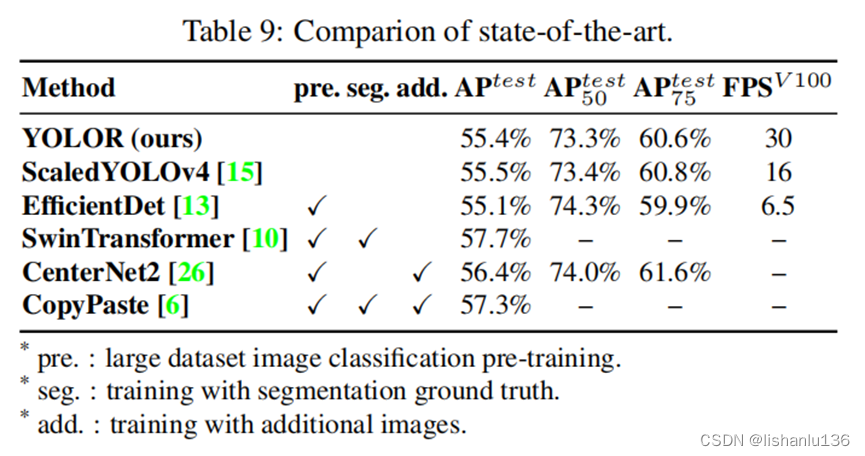
目标检测——YOLOR算法解读
论文:YOLOR-You Only Learn One Representation: Unifified Network for Multiple Tasks 作者:Chien-Yao Wang, I-Hau Yeh, Hong-Yuan Mark Liao 链接:https://arxiv.org/abs/2105.04206 代码:https://github.com/WongKinYiu/yolo…
Python界面库Flet(1)介绍和快速使用
Python界面库Flet(1)快速上手使用 Author:Once Day Date:2024年3月19日 一位热衷于Linux学习和开发的菜鸟,试图谱写一场冒险之旅,也许终点只是一场白日梦… 漫漫长路,有人对你微笑过嘛… 全系列文章可参考专栏: Pyt…
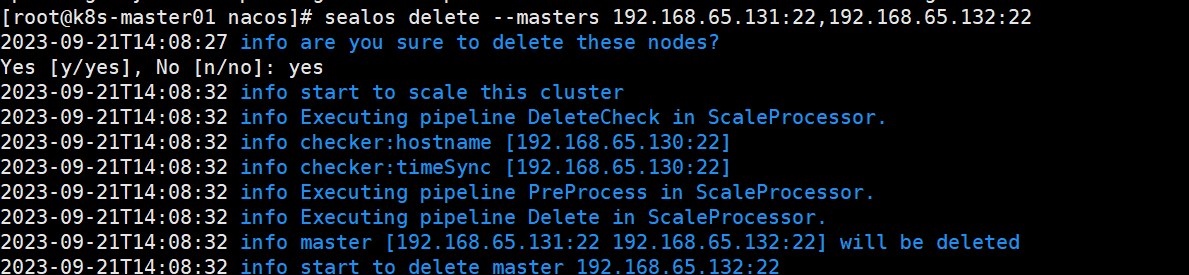
利用sealos安装k8s集群
1. 环境准备 准备三台干净(未安装过k8s环境)的虚拟机
# 所有的主机都要配置主机名和域名映射
# 设置主机名
hostnamectl set-hostname k8s-master01 # vim /etc/hosts
192.168.59.201 k8s-master01
192.168.59.202 k8s-worker01
192.168.59.203 k8…
飞鸟写作能用吗 #笔记#笔记
飞鸟写作是一个强大的论文写作工具,不仅可以帮助用户高效、准确地完成论文写作,还能帮助用户对论文进行查重和降重。那么,飞鸟写作能用吗?答案是肯定的,飞鸟写作非常好用! 首先,飞鸟写作拥有强大…
视频记录历史播放位置效果
简介
每次打开页面视频从上一次的播放位置开始播放
利用lodash库做节流
代码
<!DOCTYPE html>
<html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-sca…
MySQL | 视图
视图是一个虚拟表,其内容由查询定义。同真实的表一样,视图包含一系列带有名称的列和行数据。视图的数据变化会影响到基表,基表的数据变化也会影响到视图。
1. 基本使用
1.1. 创建视图
create view 视图名 as select语句; 创建测…
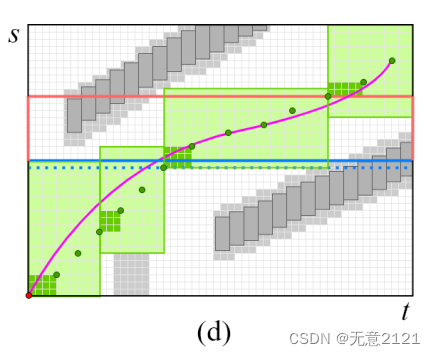
自动驾驶轨迹规划之时空语义走廊(一)
欢迎大家关注我的B站:
偷吃薯片的Zheng同学的个人空间-偷吃薯片的Zheng同学个人主页-哔哩哔哩视频 (bilibili.com)
目录
1.摘要
2.系统架构
3.MPDM
4.时空语义走廊
4.1 种子生成
4.2 具有语义边界的cube inflation
4.3 立方体松弛 本文解析了丁文超老师…
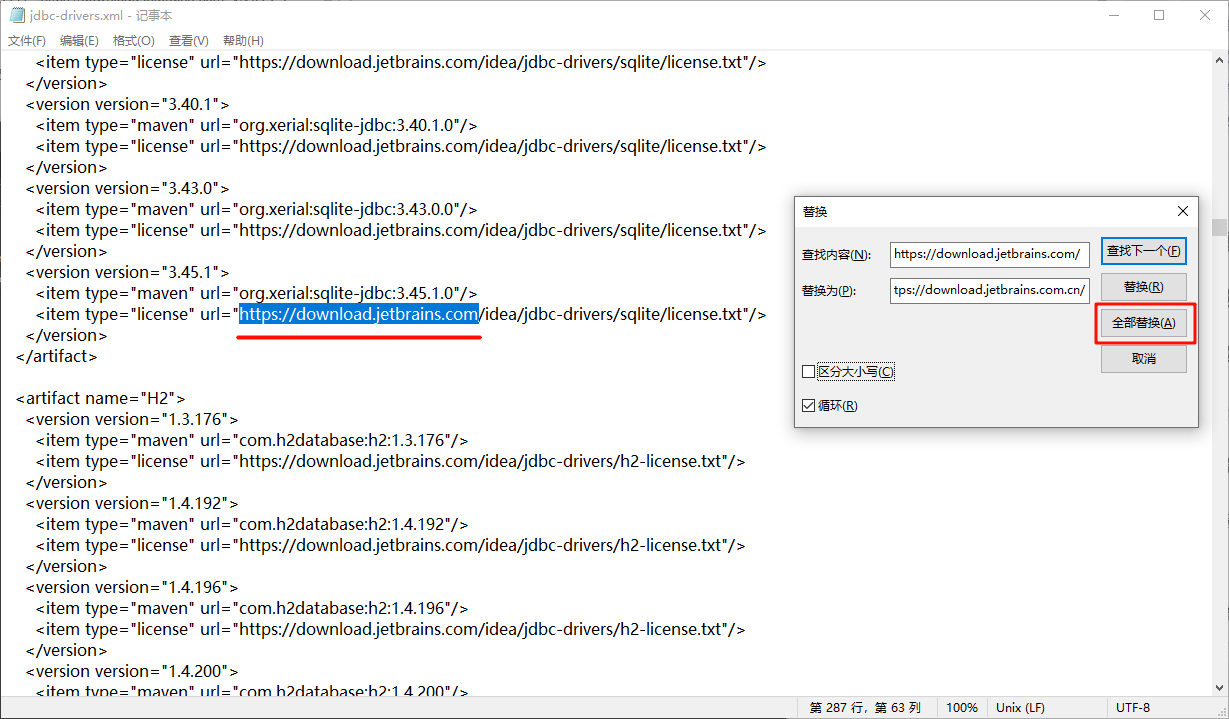
JetBrains数据库驱动下载失败解决方法
本方法可通用于解决PyCharm等JetBrains家的IDE下载数据库驱动问题。
在Jet家IDE内连接数据库时,mysql、sqlite等的驱动有部分在 https://download.jetbrains.com 网站上,可能由于网络问题无法访问。 解决方法是修改 JetBrains 路径下的 jdbc.drivers.xm…
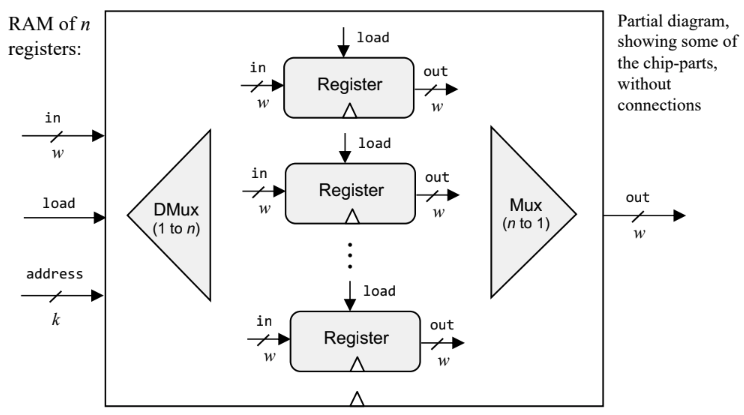
计算机基础系列 —— 从 Nand 门、DFF 到 RAM
Memory: The faculty of the brain by which data or information is encoded, stored, and retrieved when needed.It is the retention of information over time for the purpose of influencing future action —— Wikipedia 文中提到的所有实现都可以参考:nan…
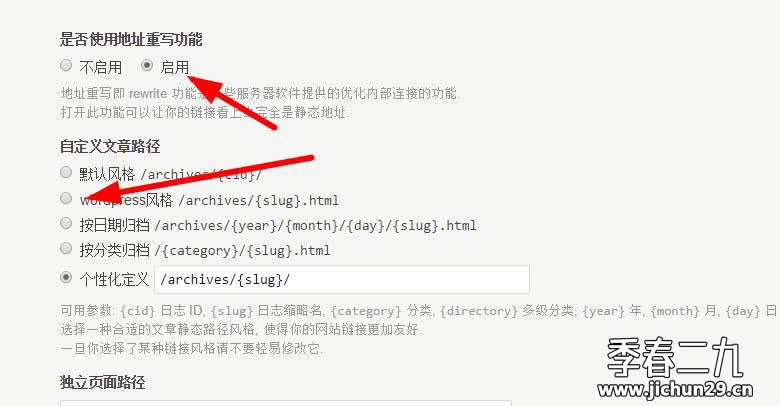
Typecho如何去掉/隐藏index.php
Typecho后台设置永久链接后,会在域名后加上index.php,很多人都接受不了。例如如下网址:https://www.jichun29.cn/index.php/archives/37/,但我们希望最终的形式是这样:https://www.jichun29.cn/archives/37.html。那么…
【Oracle】Linux——Centos7安装Oracle12c
安装前拍快照、安装前拍快照、安装前拍快照 目录 安装前拍快照、安装前拍快照、安装前拍快照1.下载Oracle12C安装包2.基本环境搭建2.1创建用户和组2.2创建oralce安装目录,oracle用户分配目录权限2.3上传安装包 3.系统参数配置及服务器设置3.1依赖安装3.2内核参数配置3.3配置完成…
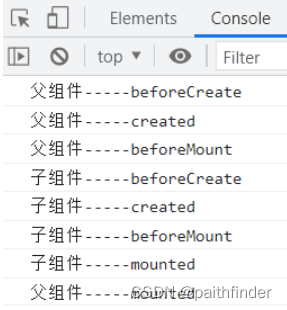
【项目自我反思之vue的组件通信】
为什么子组件不能通过props实时接收父组件修改后动态变化的值 一、现象二、可能的原因1.响应式系统的限制2.异步更新队列3.父组件和子组件的生命周期4.子组件内部对 props 的处理 三、组件通信的几种场景(解决方案)1.子组件想修改父组件的数据2.子组件传…
Keepalive与idle监测及性能优化
Keepalive 与 idle监测
Keepalive(保活): Keepalive 是一种机制,通常用于TCP/IP网络。它的目的是确保连接双方都知道对方仍然存在并且连接是活动的。这是通过定期发送控制消息(称为keepalive消息)实现的。如果在预定时…
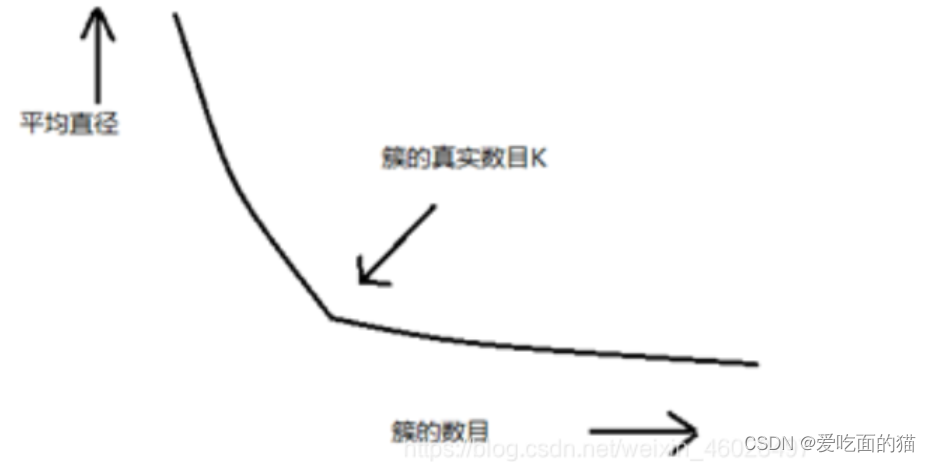
机器学习K-means算法
K-Means 算法(K-Means算法、K-Means 中心值计算、K-Means 距离计算公式、K-Means 算法迭代步骤、K-Means算法实例)
问题引入 给你如下两种图片,快读回答2个问题,问 图1 中有几类五谷杂粮?问 图2 中有几类五谷杂粮&…
深度分析鸿蒙应用开发的准确红利期、前景、未来发展方向
近年来,随着互联网技术的不断发展,鸿蒙生态开发逐渐成为热门话题。作为一种新兴的操作系统,其发展趋势备受关注。同时,鸿蒙生态开发的价值、就业岗位需求以及相关学习方面也引起了广泛关注。
那么就目前的形势来看,鸿…
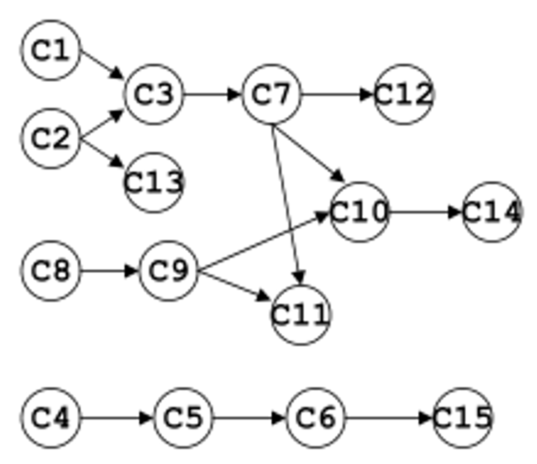
6-191 拓扑排序
一项工程由一组子任务构成,子任务之间有的可以并行执行,有的必须在完成了其他子任务后才能执行。例如,下图表示了一项工程若干子任务之间的先后关系。 编写函数输出所有子任务的拓扑序列。
函数接口定义:
Status Push_SeqStack(SeqStack &s, ElemType x)//入栈,x入到…
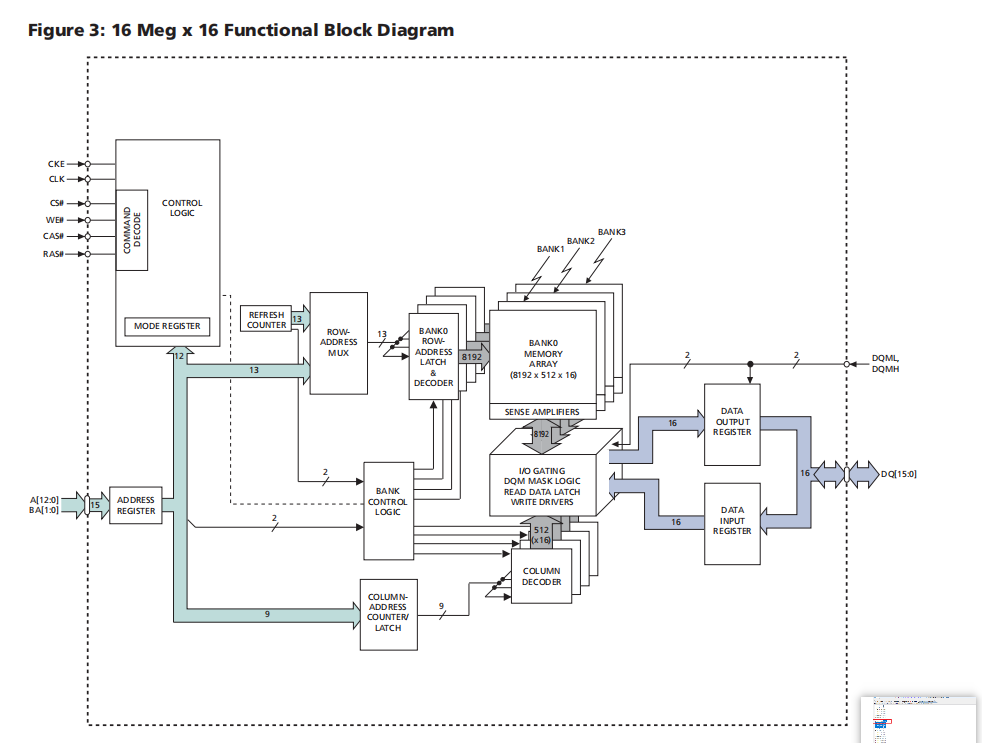
镁光的sdram手册阅读--MT48LCC16M16A2
镁光的sdram手册阅读–MT48LCC16M16A2
一、这个sdram的总容量是256Mb,MT48LC16M16A2对应的参数是:4Meg 16 4banks,也可表示为16M16。4164256Mbit。
1)其中,4Meg表示单个bank包含的存储单元个数,计算公式…
docker 数据卷 (二)
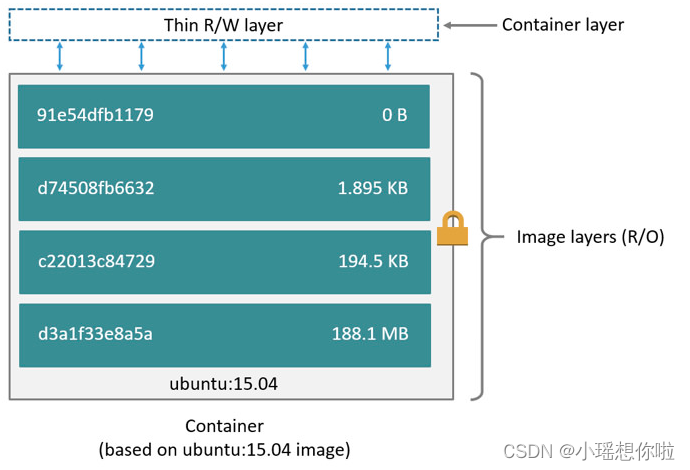
1,为什么使用数据卷
卷是在一个或多个容器内被选定的目录,为docker提供持久化数据或共享数据,是docker存储容器生成和使用的数据的首选机制。对卷的修改会直接生效,当提交或创建镜像时,卷不被包括在镜像中。
总结为两…
下载最新VMware,社区版本(免费)
VMware - Delivering a Digital Foundation For BusinessesRun any app on any cloud on any device with a digital foundation built on VMware solutions for modern apps, multi-cloud, digital workspace, security & networking.https://www.vmware.com/
官网地址
高等数学基础篇(数二)之微分方程
微分方程:
一、常微分方程的基本概念
二、一阶微分方程
三、可降阶的高阶方程
四、高阶线性微分方程 目录
一、常微分方程的基本概念
二、一阶微分方程
三、可降阶的高阶方程
四、高阶线性微分方程 一、常微分方程的基本概念 二、一阶微分方程 帮助理解&…