K-Means 算法（K-Means算法、K-Means 中心值计算、K-Means 距离计算公式、K-Means 算法迭代步骤、K-Means算法实例）

问题引入

       给你如下两种图片，快读回答2个问题，问 图1 中有几类五谷杂粮？问 图2 中有几类五谷杂粮？

                        图1                                                                              图 2 

       问 图1 中有几类五谷杂粮？你的回答会很快，是 6 类。

       问 图2 中有几类五谷杂粮？你的回答会慢一些，因为你会看一下，想一会再分一下类（红豆、绿豆、黑米、大米、花生、莲子、花豆）最后再回答。

       问题1 回答快的原因是 图中已经分好类，只需数一下。

       问题2 回答慢的原因是 图中未进行分类，需要自己进行分类。

     

       那么问题来了，让你将图2 中的五谷杂粮像图1中一样分好堆，需要分几堆呢？又如何快速的分堆呢？分堆的过程是如何分的呢？

       首先我们确定要分的堆数是7堆（红豆、绿豆、黑米、大米、花生、莲子、花豆）。

       其次我们要先确定红豆、绿豆、黑米、大米、花生、莲子、花豆各自的中心点，以各自的中心点进行抓取，这样分堆对快。例如下图中，红色中心点是大米区域的中心点，以这个为中心，距离这个中心点近的大米比较多。其他的以此类推。     

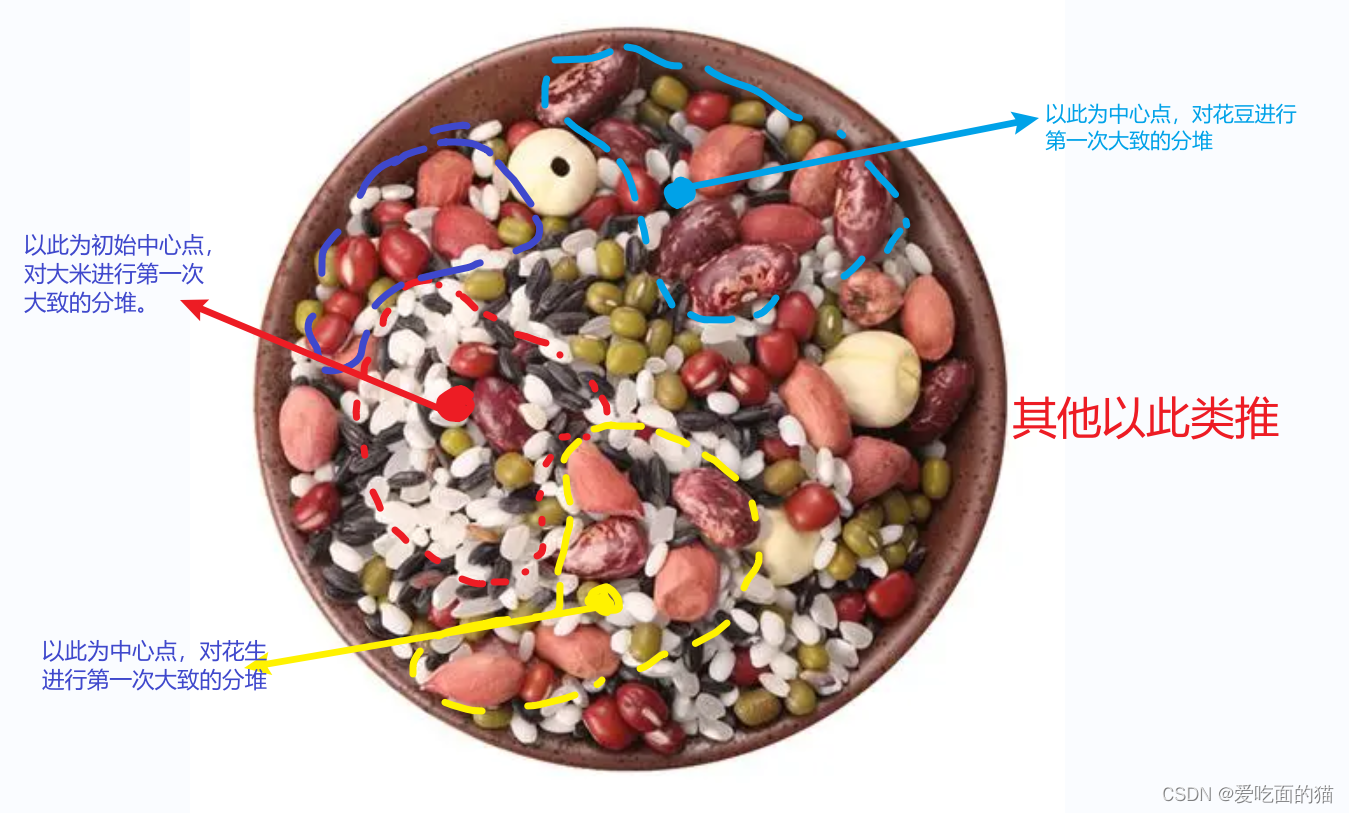
                                                                       图 3

       第一次是进行大概的分堆，没堆里面还有其他的杂粮。需要再次的进行获取中心点再次的进行划分。以此类推，直到所有的五谷杂粮都大概（每堆中可能含有少量的其他种类）分完堆。

                                                                       图 4

正题

       接下来把上述的过程交给机器，让机器自己来完成。使用的就是机器学习中的K-means算法。

• k-means  即 k均值聚类算法（k-means clustering algorithm）
• k-means 将样本数据分成不同的簇（例如 图2 中将五谷杂粮分堆）
• k-means 目标：将样本分组成具有相似特征的聚类（如将五谷杂粮分成红豆、绿豆、黑米、大米等几堆），使得同一聚类中的样本相似度高（如花生这堆中的花生的相似度很高）。
• k-means 核心思想：通过最小化样本点与所属聚类中心点之间距离来实现聚类。
• k-means 距离度量方法：常用距离度量方法是欧式距离（后面讲）。
• k-means 算法优化的目标：目标是所有样本点到所属聚类中心点的总距离最小化。

什么是K-means ?

        K-means 即 k均值聚类算法（k-means clustering algorithm）是一种常用的迭代求解的聚类分析算法，将杂乱无章的样本数据（如上面的 图2 中 混在一起的五谷杂粮），经过聚类分析后变得有点顺序（先无序，后有序）。

K-means原理

        K-Means 算法 原理 : 给定数据集  X（图2中五谷杂粮） , 该数据集有  n （500粒）个样本 , 将其分成  K 个聚类 （7个聚类：红豆、绿豆、黑米、大米、花生、莲子、花豆）;
        1、预设聚类数：设定预将数据分为K 个聚类
        2、中心点初始化 ：为 K 个聚类分组选择初始的中心点（例如上面 图3 中随机选取每一堆的中心点，共7个中心点） , 这些中心点称为 Means ; 可以依据经验 , 也可以随意选择 ;
        3、计算距离 : 计算  n 个样本与  K 个中心点 的距离 ; ( 共计算  n×K 次 ）
        4、聚类分组 : 每个对象与 K 个中心点的值已计算出 , 将每个对象分配给距离其最近的中心点对应的聚类 ;
        5、计算中心点 : 根据聚类分组后的样本 , 计算每个聚类的中心点（因为开始时随机给定的中心点，现在需要重新设定） ;
        6、迭代直至收敛 : 迭代执行 3、4、5步骤 , 直到 聚类算法收敛（所有样本点到所属聚类中心点的总距离最小化） , 即 中心点 和 分组 经过多少次迭代都不再改变 , 也就是本次计算的中心点与上一次的中心点一样 ;

 常用距离度量方法是欧式距离，公式如下：

K-means原理分析案例

        数据集：5个数据  { X1 , X2 , X3 , X4 , X5 }    分为2个类

        选取中心点：k1 和 k2 （注意，也可以是样本数据本身，如x1）

        计算  5 个点到  2 个中心点的距离 , 每个点都要计算  2 次 , 共计算  10 次 ;

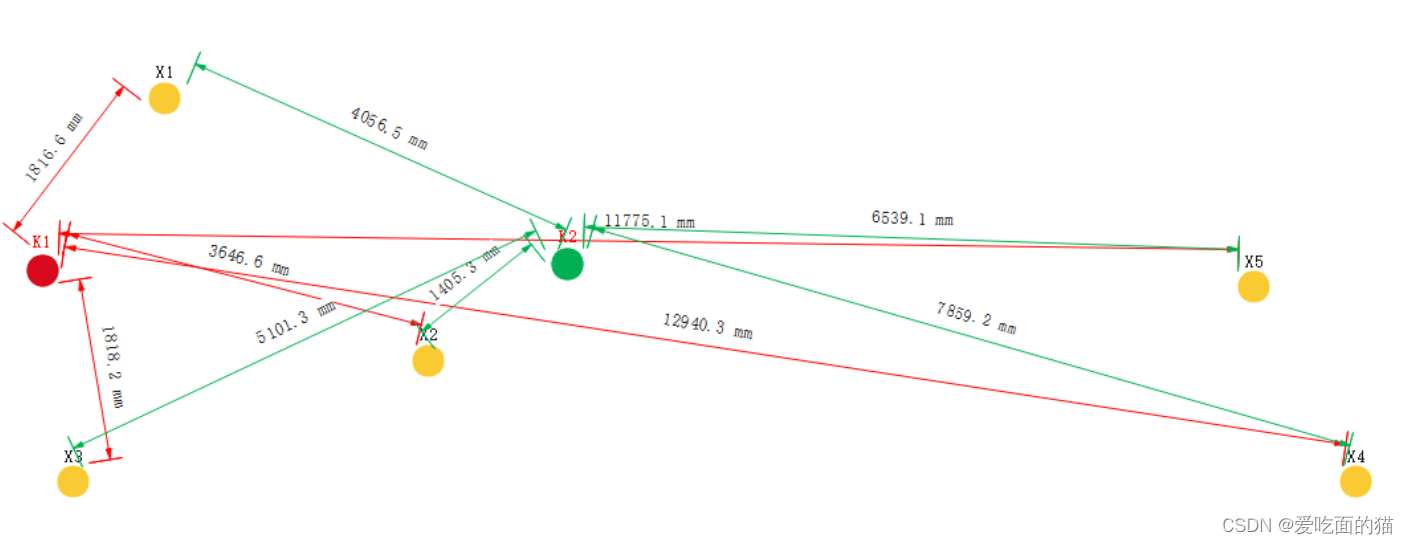
        进行初步分组 : 根据{ X1 , X2 , X3 , X4 , X5 }分别到 k1 和 k2 的距离远近，进行初步为每个样本分组 , 将 样本点  { X1 , X2 , X3 , X4 , X5 } 分到最近的中心点对应的聚类分组中 , 如： X1​,X3​ 到k1中心点距离近，分组到  K1​ 中心点对应的分组 , 同理X2,X5​,X4​ 分到  K2​ 对应的分组 ，新的分组是 {X1​,X3​} ,  {X2​,X5​,X4​} ;

       重新选取中心点，红色组中心点为 k1，绿色组中心点为k2，计算{ X1 , X2 , X3 , X4 , X5 }分别到k1和k2的距离

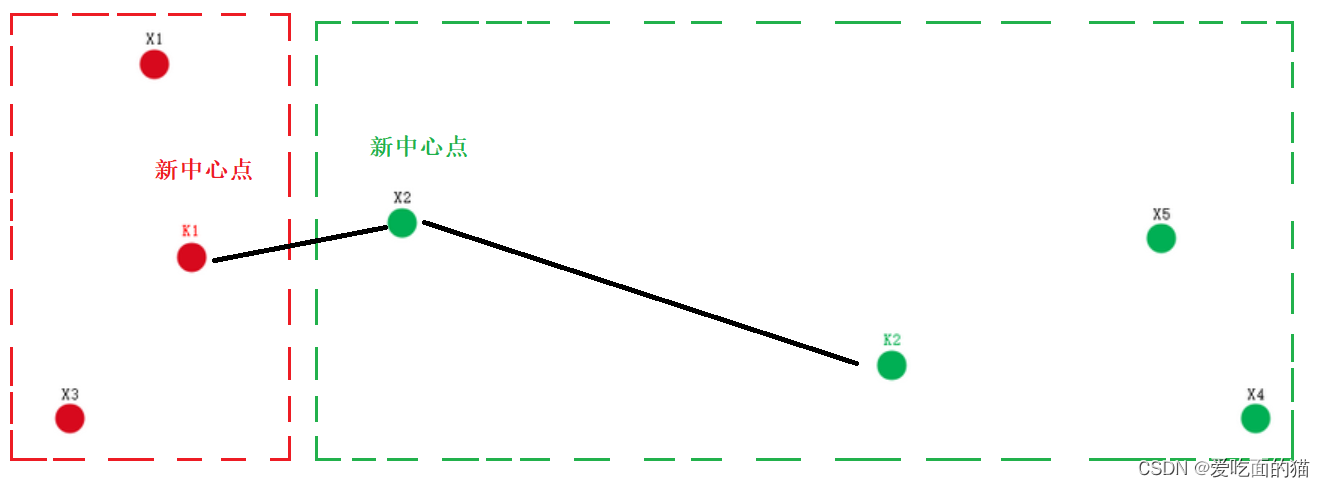
         计算后 X2 距离新的中心点k1比较近，X5,X4距离中心点k2比较近，进行重新分组。

        继续选取新的中心点，分组后的效果和上面一样，因此这个中心点就比较稳定了 , 下一次计算 , 仍然是这个中心点 , 因此 聚类收敛 , 此时的分组就是最终的聚类分组 ; 

最优中心点

        通过上面我们知道，什么样的中心点是最优中心点呢？就是样本点到所属聚类中心点的总距离最小化。在进行讲解之前了解及个距离：

• 曼哈顿距离：就是两个值相减取绝对值 ，

       一维数据：{1,2,3,10,11,12}中 1和 10 的距离 d=|10-1|
       二维数据：{A1​(2,4) , A2​(3,7) } A1 和A2 的距离 d=|2-3|+|4-7|

• 欧几里得距离：两点之间距离

       二维数据：{A1​(X1,y1) , A2​(X2,y2) }

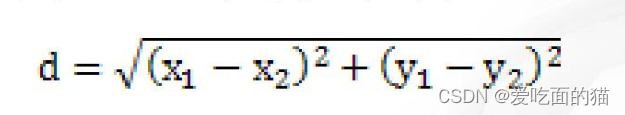
     N维数据：

         

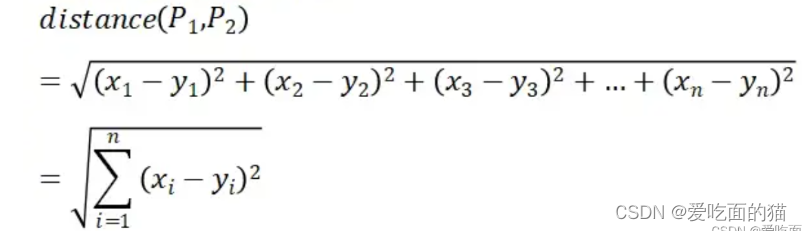
       k-means 的目标是将样本分组成具有相似特征的聚类，使得同一聚类中的样本相似度高即样本点到所属聚类中心点的距离最小化。而 k-means 算法常用欧氏距离作为样本之间距离的度量，那么也就是只要上面公式距离最小，开方后距离也最小，因此可以写成如下格式：

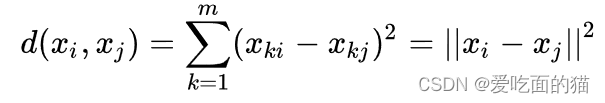
        k-means 的目标是所有样本点到所属聚类中心点的总距离最小化，那么损失函数定义为样本与其所属类的中心之间的距离的总和：

K-means算法实现

import numpy as np
class Kmeans: 
 def __init__(self, k):  
   self.k = k   
    self.cendroids = None​  
    def distance(self, x1, x2):   
    return np.sqrt(np.sum(np.square(x1 - x2), axis=-1))​ 
    def fit(self, X, max_iter=500):   
     '''    
     Input:      X: np.array, shape=[N, dim]  
     output:      cluster: np.array, shape=[N,]  
     '''   
        N, dim = X.shape   
         # 随机选择样本作为初始簇中心  
         cendroids = np.zeros((self.k, dim))  
         for i in range(k):     
         cendroids[i, :] = X[int(np.random.uniform(0, N)), :]  
         # 迭代   
         for _ in range(max_iter):      
         pre_cendroids = cendroids      
         distances = self.distances(X[:, None, :], cendroids[None, :, :])      
         clusters = np.argmin(distances, axis=1)      
         for k in range(self.k):       
         cendroids[k, :] = np.mean(X[clusters == k, :])    
           if pre_cendroids == cendroids:     
              break​    
              self.cendroids = cendroids    
              return clusters

K-means算法应用场景及注意事项

        数据集中存在自然的群集结构： K-means假设数据可以被分为若干个紧密聚集的群集，适用于数据集中存在簇结构的情况。
        对计算效率要求较高： K-means是一种计算效率较高的算法，特别是对于大型数据集。它通常是大规模数据集聚类的首选算法之一。
        簇的形状近似为球形： K-means对于各向同性（球形）簇的效果较好。如果簇的形状非常复杂或者簇之间有重叠，K-means的性能可能会下降。
        对于划分性质的问题： K-means适用于将数据点划分为互不重叠的簇的问题，每个数据点只属于一个簇。
        对于初始聚类中心的选择不敏感时： 尽管K-means对于初始聚类中心的选择较为敏感，但在某些情况下，算法的性能可能对初始值不太敏感，或者可以通过多次运行算法以获取不同初始值的结果。
        注意：K-means并不适用于所有类型的数据和问题。在一些情况下，数据可能不满足K-means的假设，或者聚类的数量不容易确定。在这些情况下，其他聚类算法或深度学习方法可能更为合适。在应用K-means之前，最好先对数据进行探索性分析，确保它满足算法的假设。

K-means算法案例分析

       Python实现K-means聚类，使用机器学习库如scikit-learn。案例代码如下：

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# 生成模拟数据
n_samples = 300
n_features = 2
n_clusters = 3

# 使用make_blobs生成聚类数据
X, y = make_blobs(n_samples=n_samples, n_features=n_features, centers=n_clusters, random_state=42)

# 使用KMeans算法进行聚类
kmeans = KMeans(n_clusters=n_clusters)
kmeans.fit(X)

# 获取聚类结果和聚类中心
labels = kmeans.labels_
centers = kmeans.cluster_centers_

# 绘制原始数据和聚类结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', edgecolor='k')
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='X', s=200, label='Centroids')
plt.title('K-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()

模型优化以及思考

        k-means算法严重问题之一就是初始点的选取问题，在此处，也许会有优化之处，此处提出两点优化。
       1.第一种优化方式在第一个点的选取处进行优化，第一个点可以挑选密度最大处的中心点，从而避免了出现离群点的问题，但是在此方法中选取我们需要选择一个合适区域（或者说选取合适的半径）.第二个点则需要选取距离此点最远的点最为第二个中心点。第三个点则选取距离两点最远的点作为第三个点。以此类推，直到选取出K个初始聚类中心。
        2.第二种改进方式是选取出密度最大的点，然后减去它周围最近的n个点（n的值是数据总数除以K），然后再找到剩余数据中密度最大的点，再减去它周围的n个点，以此类推，直到选取完成，此方法的局限性很大，基本选取完成之后，聚类的簇已经非常明显了。而且一般适用于三维以下的数据，三维以下的数据均可以在图像中表示出来，但四维以上的数据很难直观的观察。

        k-means算法选取初始点k值的简单方法：
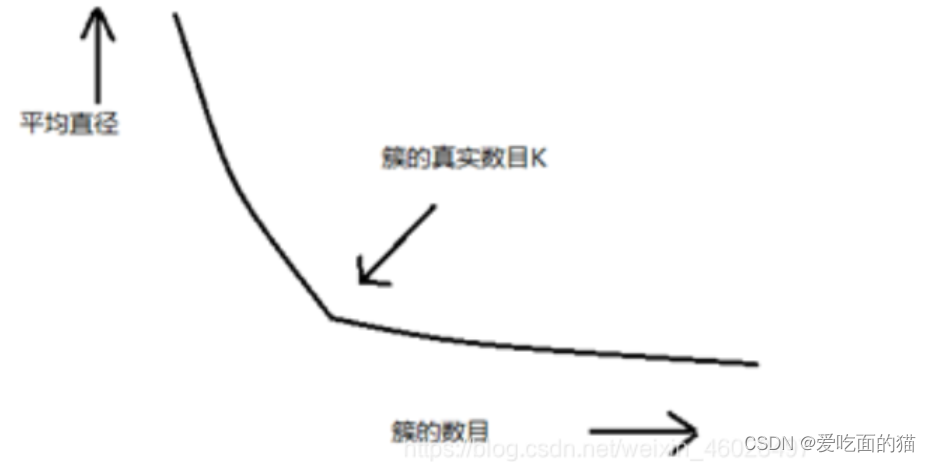
        在使用k-means算法时我们很难根据经验法对k值进行确定，而且在一般的比赛中使用经验法是极其不现实的。因此，我们可以观察不同k值情况下，每个簇中每个点到中心点的平均距离，当k的值大于真实数目时，平均距离上升速度会上升的很缓慢，但是当k值小于真实数目时，平均距离会急剧上升。

K-Means 算法变种（了解）

        1 K-Means 方法有很多变种 :
        ① K_Modes : 处理离散型的属性值 , 如字符型数据等 ;
        ② K-Prototypes : 处理 离散型 或 连续型 的属性 ;
        ③ K-Medoids : 其计算中心点不是使用算术平均值 , 其使用的是中间值 ;

        2、 K-Means 变种算法 与 k-Means 算法的区别与联系 :
        ① 原理相同 : 这些变种算法 与 K-Means 算法原理基本相同 ;
        ② 中心点选择不同 : 变种算法 与 原算法 最初的中心点选择不同 ;
        ③ 距离计算方式不同 : K-Means 使用曼哈顿距离 , 变种算法可能使用 欧几里得距离 , 明科斯基距离 , 边际距离 等 ;
        ④ 计算聚类中心点策略不同 : K-Means 算法中使用算术平均 , 有的使用中间值 ;