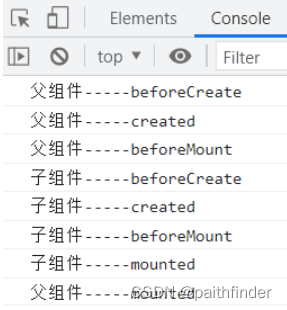
欢迎大家关注我的B站：

偷吃薯片的Zheng同学的个人空间-偷吃薯片的Zheng同学个人主页-哔哩哔哩视频 (bilibili.com)

目录

1.摘要

2.系统架构

3.MPDM

4.时空语义走廊

​4.1 种子生成

4.2 具有语义边界的cube inflation

​4.3 立方体松弛

---

本文解析了丁文超老师的这篇论文Safe Trajectory Generation for Complex Urban Environments Using Spatio-Temporal Semantic Corridor | IEEE Journals & Magazine | IEEE Xplore

1.摘要

引入：城市道路轨迹规划的难点在于有很多语义元素。

创新点1：不同的语义元素有不同的数学表征形式，提出了一种新的统一的时空语义走廊来为不同类别的语义元素来提供abstraction，可以推广到任何语义元素组合的场景。

创新点2：SSC由一系列互相连接的无碰撞cubes组成，其中包含了动态约束，并且轨迹生成问题可以归结于一个QP问题，并且通过贝塞尔曲线来保证轨迹安全性和可行性。

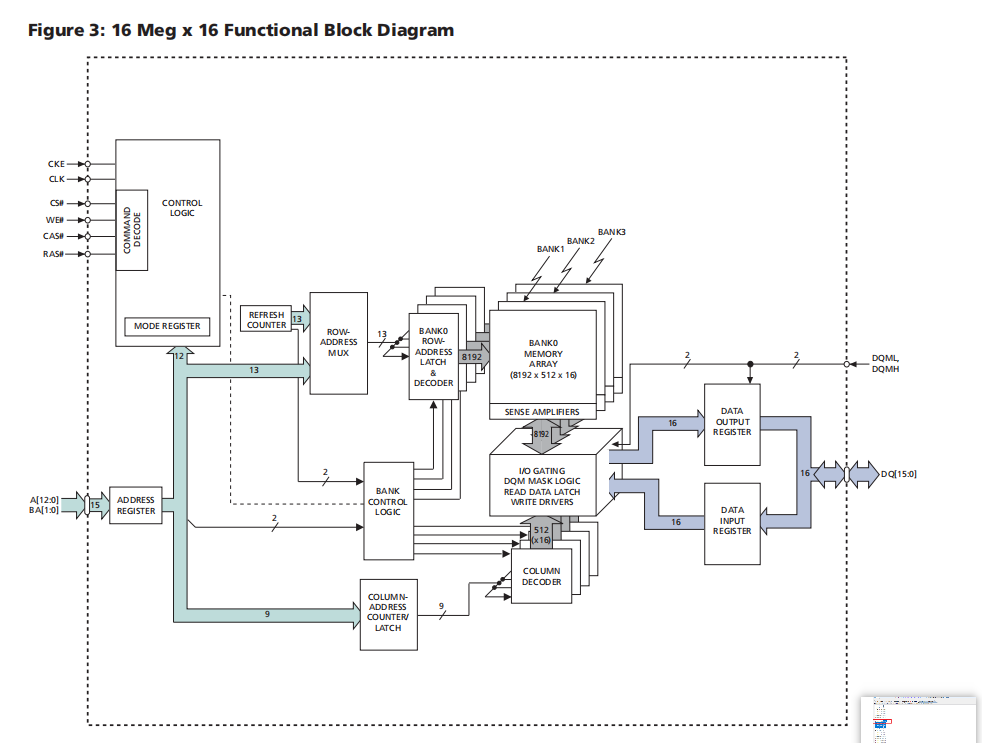
2.系统架构

第一阶段：环境理解，通过语义地图管理器管理用于本地规划目的的语义要素

第二阶段：包含自车high-level的行为预期以及他车预测轨迹的预测器

第三阶段：利用多策略决策的行为规划器

第四阶段：离散未来状态作为生成走廊的种子的运动规划器

3.MPDM

行为规划问题被被表述为多智能体的POMDP问题，来对动态环境中的交互和不确定性进行建模。但是当车辆数量增加，计算负担会很重。MDPM将问题简化为有限的闭环离散策略（如向左变道，车道保持等）。自车和他车都在执行简单的策略。

自车和他车的预测都通过简化的模型前向模拟来实现，并且结合理想化的转向和速度控制器来评估最佳行为。而自车的前向模拟状态是走廊生成过程中的种子。由于粗糙的分辨率和简化的模型，这不能直接由车辆执行，这也是轨迹生成器的必要性。

MPDM同时为多个行为提供前向模拟，我们为所有潜在行为生成候选轨迹。

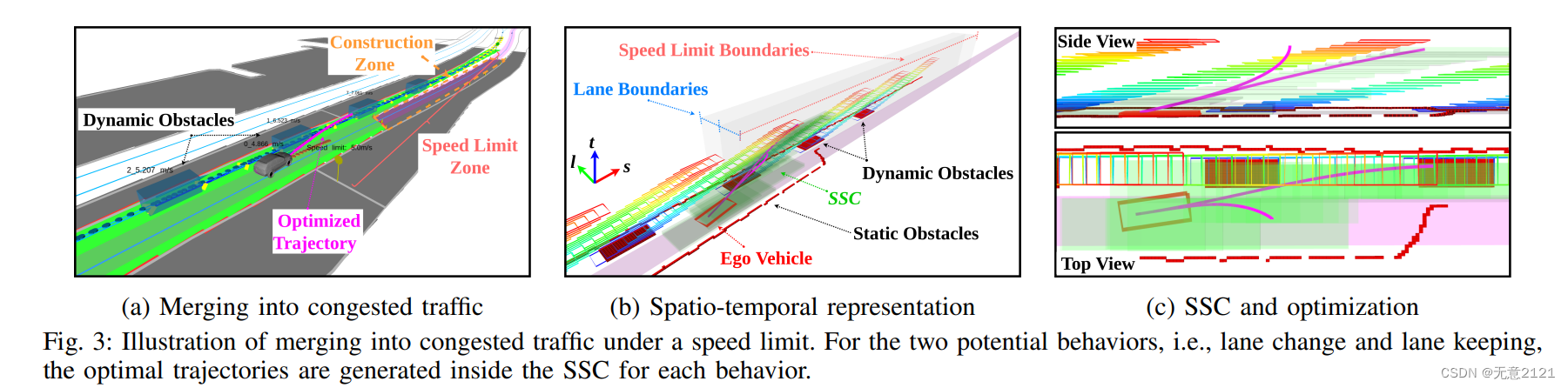
4.时空语义走廊

由于大多数语义元素都与车道几何结构有关，因此我们需要将笛卡尔坐标系转换到基于参考车道的frenet坐标系，并且对于时空联合规划我们将处理一个SLT三维配置空间。语义主要有obstacle-like和constraint-like两类元素。障碍物就是slt空间内不允许驶入的空间，约束就是一些速度限制等。而语义边界可以对所有constraint-like的元素进行统一的表示。

下图则是走廊生成的算法流程

4.1 种子生成

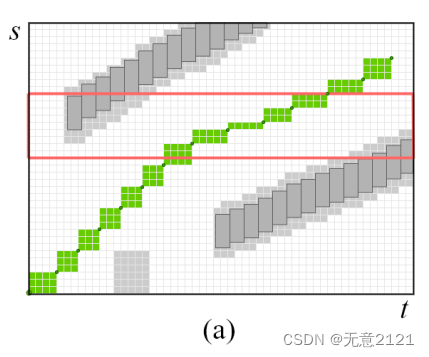
种子是由行为规划器中前向模拟状态投影到SLT空间下得到的。我们要求连续种子构建的初始立方体无碰撞，例如，对于以30m/s的纵向速度和0.15s的种子分辨率，所需的间隙约为4.5m，这比需要的紧急制动距离短得多。因此，如果有碰撞直接驳回的判断是合理的。

而在种子周围生成走廊的动机是对拓扑等效的自由空间进行建模。比如这张图显示了种子的拓扑含义是在这两个动态障碍物之间通行。由于膨胀在碰到语义边界或障碍物后停止，因此膨胀过后的走廊的同伦与种子是一样的。

4.2 具有语义边界的cube inflation

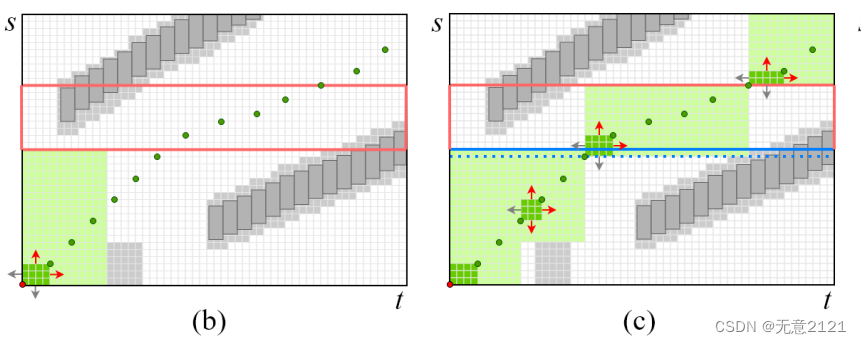
初始立方体是通过两个连续的种子生成的，立方体的膨胀是在碰到障碍物与语义边界时停止。这样处理使得不在语义边界内的立方体不用考虑约束，在语义边界的立方体直接关联约束。未来保持凸性，立方体之间没有重叠。但也可以引入时间进行优化，重叠可能是有益的。

4.3 立方体松弛

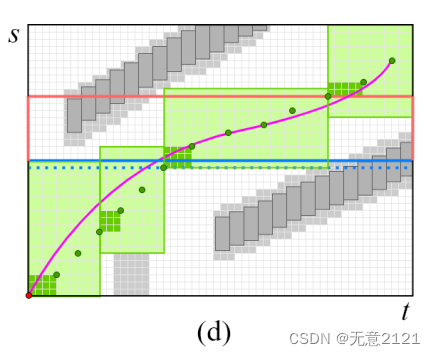
在立方体膨胀过程之后，膨胀的立方体几乎与语义边界匹配，但比如变道持续时间约束等都是软约束，我们可以通过cube relaxation来松弛边界，但要保持硬约束和无碰撞。允许松弛的最大裕度一般由两个连续立方体结合运动学去估计。

下一次将介绍轨迹生成与实验