[ C++ ] STL---仿函数与priority_queue

news2024/11/14 8:32:12

目录

仿函数

示例一：

示例二 :

常见的仿函数

priority_queue简介

priority_queue的常用接口

priority_queue的模拟实现

基础接口

push()

堆的向上调整算法

堆的插入

pop()

堆的向下调整算法

堆的删除

priority_queue最终实现

仿函数

仿函数（Functor）是一个类/结构体，其内部重载了operator()运算符，使其可以像函数一样被调用；

  1. 由于模版参数接收类型，仿函数是一个类，可以通过 类名/类名<数据类型> 传递给模版参数；
  2. 仿函数是一个类，则其可以定义对象，对象调用operator()完成控制作用；

示例一：

//带模版参数的仿函数
template<class T>
struct Greater
{
	//重载operator()
	bool operator()(const T& x, const T& y)
	{
		return x > y;
	}
};
void Func()
{
	int x = 10;
	int y = 20;
	//创建一个仿函数对象
	Greater<int> Great;
	//通过对象调用仿函数
	cout << Great(x, y) << endl;
	//cout<<Great.operator()(x,y)<<endl;
	//通过匿名对象调用仿函数
	cout << Greater<int>()(x, y) << endl;
}
int main()
{
	Func();
	return 0;
}

示例二 :

//此模版参数接收数据类型
template<class T>
struct Greater
{
	//重载operator()称为仿函数/函数对象
	bool operator()(const T& x, const T& y)
	{
		return x > y;
	}
};
//此模版参数接收仿函数类型
template<class compare>
class A
{
public:
	void func(int a, int b)
	{
		compare com;
		cout << com(a, b) << endl;
		//com(a,b)--->com.operator()(a,b)--->com为仿函数对象
	}
};

int main()
{
	//A类中传递仿函数类型Greater<T>-->仿函数类中传递数据类型Greater<int>
	A<Greater<int>> aa1;
	aa1.func(10, 20);

	A<Greater<int>>aa2;
	aa2.func(20, 10);
	return 0;
}

具有相同功能的代码可以在不同的类中用到，但是不好将功能相同的代码实现成某一个类的成员函数，仿函数实现了一个简单的类，将需要复用的代码实现在operator()重载函数中，外部函数需要使用时只要用这个类实例化出一个对象，就可以像使用函数一样来使用这个对象，完成对应功能；

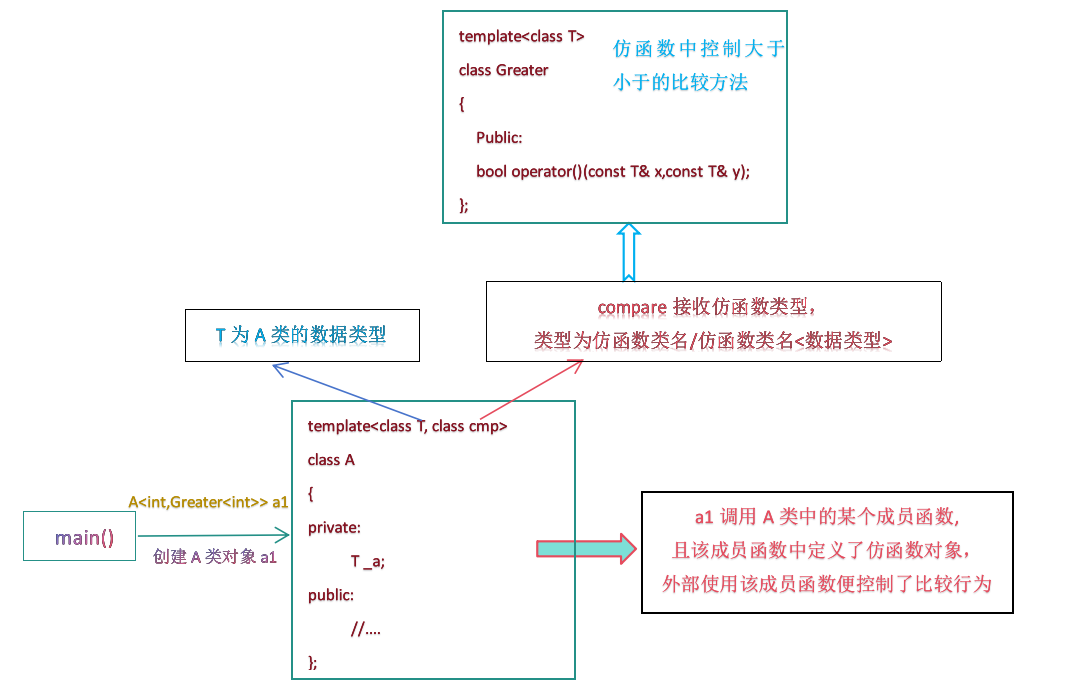
常见的仿函数

template <class T> 
struct less 
{
  bool operator() (const T& x, const T& y) const 
  {
       return x<y;
  }
};
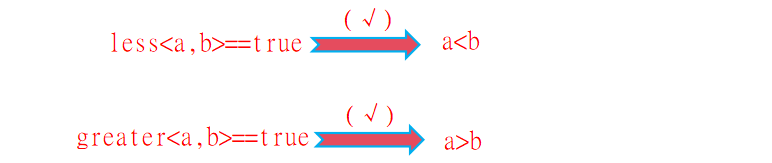
//std::less<T>: 对于基本数据类型和自定义类型，默认使用<运算符进行比较;

template <class T> 
struct greater 
{
  bool operator() (const T& x, const T& y) const 
  {
       return x>y;
  }
};
//std::greater<T>: 对于基本数据类型和自定义类型，默认使用>运算符进行比较;

除了c++标准库所提供的仿函数外，可以自定义仿函数来实现自定义的元素比较规则，自定义仿函数需要满足严格弱排序的要求，即：

  • 比较关系必须是可传递的：对于任意元素a、b和c，如果a与b比较相等，b与c比较相等，则a与c比较也相等；
  • 比较关系不能是部分顺序：对于任意元素a和b，它们不能同时大于、小于或等于彼此；
  • 比较关系必须是可比较的：比较关系的结果必须对所有元素定义明确的大小关系；

priority_queue简介

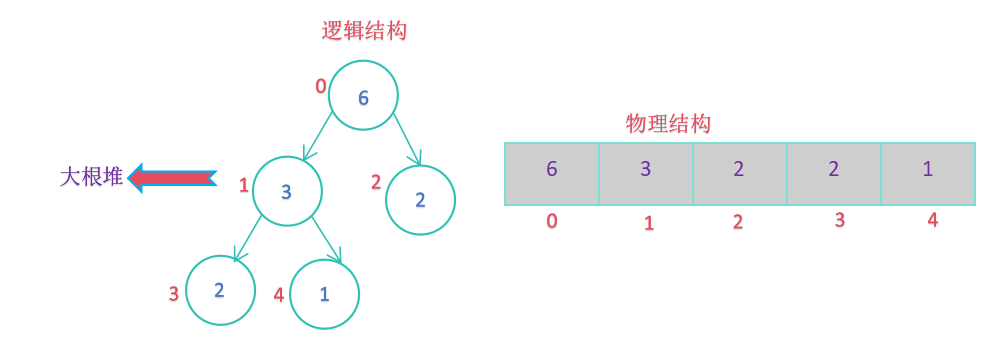
1. 优先队列是一种容器适配器，根据严格的弱排序标准，它的第一个元素总是它所包含的元素中最大的；

2. 优先队列的底层数据结构为堆，在堆中可以随时插入元素，并且只能检索最大堆元素(优先队列中位于顶部的元素)；

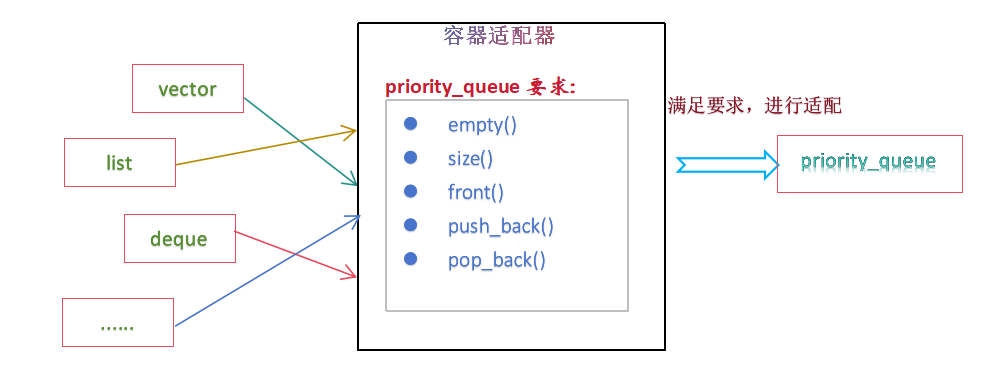
3. 优先队列被实现为容器适配器，容器适配器即将特定容器类封装作为其底层容器类，queue提供一组特定的成员函数来访问其元素，元素从特定容器的"尾部"弹出，其称为优先队列的顶部；

4. 底层容器可以是任何标准容器类模板，也可以是其他特定设计的容器类，容器应该可以通过随机访问迭代器访问，并支持以下操作:

  • empty()：检测容器是否为空
  • size()：返回容器中有效元素个数
  • front()：返回容器中第一个元素的引用
  • push_back()：在容器尾部插入元素
  • pop_back()：删除容器尾部元素

5. 标准容器类vector和deque满足这些需求；默认情况下，如果没有为特定的priority_queue类实例化指定容器类，则使用vector；

6. 需要支持随机访问迭代器，以便始终在内部保持堆结构；容器适配器通过在需要时自动调用算法函数make_heap、push_heap和pop_heap来自动完成此操作；

注意：

  1. 由于优先队列底层数据结构为堆，堆的删除是删除堆顶数据，首先将堆顶数据与最后一个数据交换位置，其次删除数组中最后一个元素，所以容器中要求pop_back()；
  2. 由于优先队列底层数据结构为堆，堆的插入是数组的尾元素的下一个位置插入数据，然后利用向上调整算法调整为堆，所以容器中要求push_back()；
  3. 默认情况下，priority_queue使用std::less作为比较函数，创建的是大堆；如果需要按照从小到大的顺序排列，可以使用std::greater作为比较函数，创建的是小堆；

堆的相关知识点回顾：CSDN

priority_queue官方文档：priority_queue - C++ Reference

priority_queue的常用接口

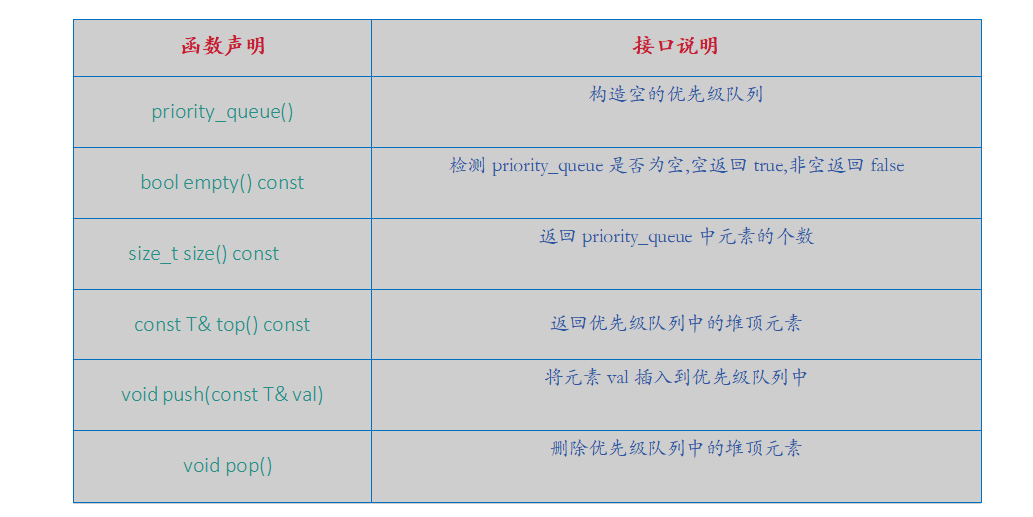
int main()
{
    //未给定仿函数比较方式,默认创建大根堆
	priority_queue<int, vector<int>> pq;
	//尾插数据
	pq.push(1);
	pq.push(2);
	pq.push(6);
	pq.push(2);
	pq.push(3);
	cout << "size=" << pq.size() << endl;
	while (!pq.empty())
	{
		//取堆顶数据
		cout << pq.top() << " ";
		//删除堆顶元素
		pq.pop();
	}
	cout << endl;
	return 0;
}

运行结果：

int main()
{
    //给定比较方式为greater,创建小根堆
	priority_queue<int, vector<int>,greater<int>> pq;
	//尾插数据
	pq.push(1);
	pq.push(2);
	pq.push(6);
	pq.push(2);
	pq.push(3);
	cout << "size=" << pq.size() << endl;
	while (!pq.empty())
	{
		//取堆顶数据
		cout << pq.top() << " ";
		//删除堆顶元素
		pq.pop();
	}
	cout << endl;
	return 0;
}

运行结果：

priority_queue的模拟实现

基础接口

#include <iostream>
#include <vector>
template<class T, class Container = vector<T>>
class priority_queue
{
public:
	//获取堆顶元素即数组首元素
	const T& top()
	{
		return _con[0];
	}
	//获取堆的数据个数即容器中的数据个数
	size_t size()
	{
		return _con.size();
	}
	//检测堆是否为空即容器是否为空
	bool empty()
	{
		return _con.empty();
	}
private:
	Container _con;
};

push()

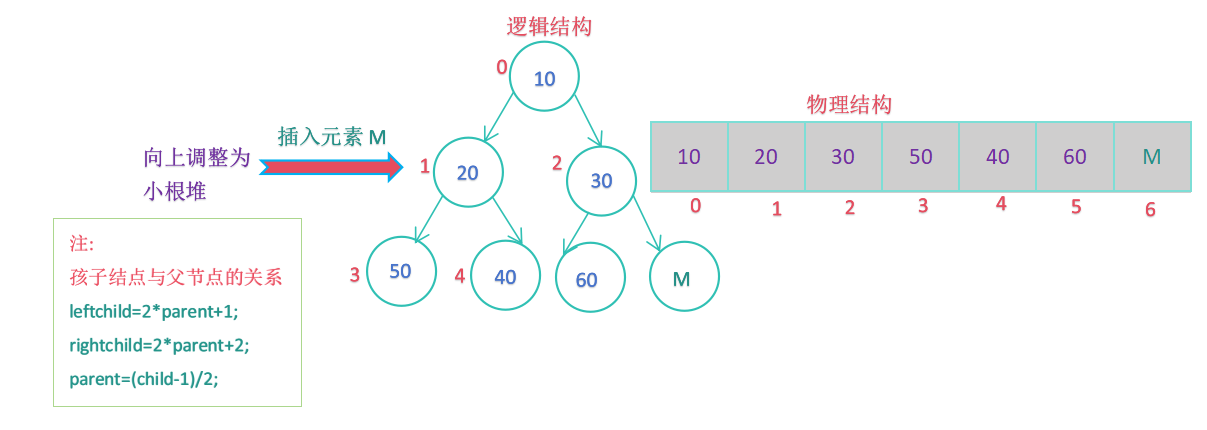
堆的存储结构为数组，尾插时间复杂度O(1)，首先将元素插入到数组的尾部，其次利用堆的向上调整算法，将数组调整为大根堆/小根堆；

堆的向上调整算法

case 1:

当插入的数值M大于其父节点的值时，仍然为小堆，此时不做任何调整；

case 2:

当插入的数值M小于其父节点的值时，破坏了堆的逻辑结构，向上调整为小堆；

（假设M=5）

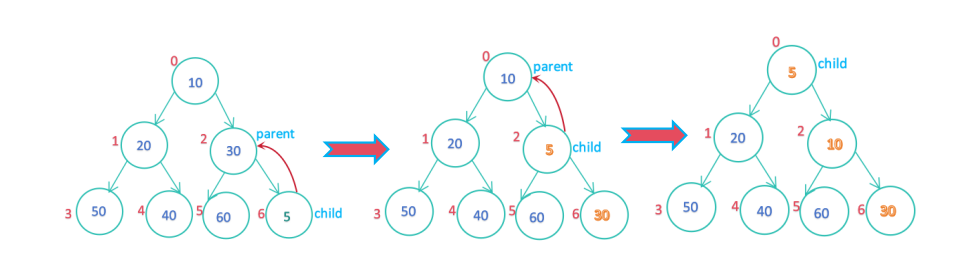
向上调整的过程中，只要出现待调整的孩子结点大于其父节点，便可停止调整，已经满足小堆的逻辑结构；

//向上调整为小堆
void adjustup(size_t child)
{
	size_t parent = (child - 1) / 2;
	while (child > 0)
	{
		if (_con[child] < _con[parent])
		{
			//交换
			swap(_con[child], _con[parent]);
			//向上走
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
//向上调整为大堆
void adjustup(size_t child)
{
	size_t parent = (child - 1) / 2;
	while (child > 0)
	{
		if (_con[child] > _con[parent])
		{
			//交换
			swap(_con[child], _con[parent]);
			//向上走
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

堆的插入

void push(const T& val)
{
	//插入数据
	_con.push_back(val);

	//从插入值为val的孩子结点的下标开始向上调整为小堆/大堆
	adjustup(_con.size()-1);
}

pop()

堆的删除是删除堆顶数据，首先将堆顶元素与堆中最后一个元素交换，其次删除堆中最后一个元素，最后将堆顶元素利用向下调整算法调整到满足其逻辑结构为堆；

注：堆的向下调整算法的前提左右子树同为小堆/同为大堆；

堆的向下调整算法

case 1：左右子树皆为小堆，向下调整为小堆；

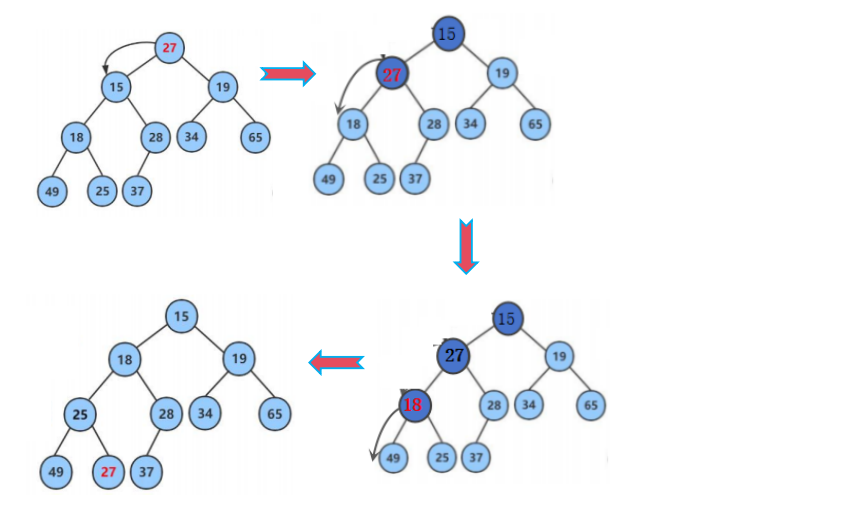
//向下调整为小堆
void adjustdown(size_t parent)
{
	size_t child = 2 * parent + 1;
	while (child < _con.size())
	{
		//假设法求同一层孩子节点最小者
		if (child + 1 < _con.size() && _con[child] > _con[child + 1])
		{
			child++;
		}
		//逻辑关系不满足小堆，交换调整
		if (_con[child] < _con[parent])
		{
			swap(_con[child], _con[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}

case 2：左右子树皆为大堆，向下调整为大堆；

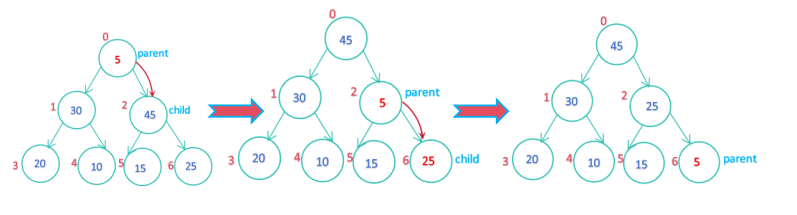
//向下调整为大堆
void adjustdown(size_t parent)
{
	size_t child = 2 * parent + 1;
	while (child < _con.size())
	{
		//假设法求同一层孩子节点最大者
		if (child + 1 < _con.size() && _con[child] < _con[child + 1])
		{
			child++;
		}
		//逻辑关系不满足大堆，交换调整
		if (_con[child] > _con[parent])
		{
			swap(_con[child], _con[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}

堆的删除

void pop()
{
	//将堆顶元素与堆中最后一个元素交换
	swap(_con[0], _con[size() - 1]);
	//删除最后一个元素
	_con.pop_back();
	//将堆顶元素利用向下调整算法调整到满足其逻辑结构为堆
	adjustdown(0);
}

priority_queue最终实现

堆分为大根堆与小根堆，向上调整算法/向下调整算法对于大根堆/小根堆的实现只有各别符号的差别，外部使用优先队列（priority_queue）时，只能在内部手动修改相应的符号来控制生成的是大堆/小堆，对于使用者而言，只能创建大堆/小堆，两者只能实现一个，故引入第三个模版参数传递仿函数类型，指定比较方式，此时使用者只需给定比较方式便可在大小堆之间自由切换；

注意：由于容器中一开始没有数据，故不用建堆，它是每插入一个数据，调用向上调整法，删除数据，调用向下调整法，不断地插入和删除，并且使其保持堆的逻辑结构 ；

#include <iostream>
#include <vector>
#include <functional>
using namespace std;
template<class T, class Container =vector<T>, class Compare = less<T>>
class priority_queue
{
public:
	bool empty() const
	{
		return _con.empty();
	}
	size_t size() const
	{
		return _con.size();
	}
	const T& top() const
	{
		return _con[0];
	}
	T& top()
	{
		return _con[0];
	}
	//向上调整算法
	void adjustup(size_t child)
	{
		size_t parent = (child - 1) / 2;
		while (child > 0)
		{
			//_con[parent]<_con[child],父节点小于其孩子节点，交换向上调整--->大堆
			if (_cmp(_con[parent], _con[child]))
			{
				swap(_con[parent], _con[child]);
				child = parent;
				parent = (child - 1) / 2;
			}
			else
			{
				break;
			}
		}
	}
	void push(const T& val)
	{
		_con.push_back(val);
		adjustup(_con.size() - 1);
	}
	//向下调整算法
	void adjustdown(size_t parent)
	{
		size_t child = parent * 2 + 1;
		while (child <_con.size())
		{
			 //child+1< _con.size()保证右孩子结点存在
			//less<T> _cmp ---> _con[child]<_con[child+1]--->child++ --->挑选大的孩子结点
			if (child + 1 < _con.size() && _cmp(_con[child], _con[child + 1]))
			{
				child++;
			}
			//_con[parent]<_con[child],父节点小于其孩子结点,交换向下调整---->大堆
			if (_cmp(_con[parent], _con[child]))
			{
				swap(_con[parent], _con[child]);
				parent = child;
				child = parent * 2 + 1;
			}
			else
			{
				break;
			}
		}
	}
	void pop()
	{
		swap(_con[0], _con[_con.size()-1]);
		_con.pop_back();
		adjustdown(0);
	}
private:
	Container _con;
	Compare _cmp;//less<T> _cmp;
};

欢迎大家批评指正，博主会持续输出优质内容，谢谢大家观看，码字画图不易，希望大家给个一键三连支持~ 你的支持是我创作的不竭动力~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1539260.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

数据结构 - 二叉树非递归遍历

数据结构 - 二叉树非递归遍历

文章目录 前言一、前序二、中序三、后序 前言 本文实现二叉树的前中后的非递归遍历&#xff0c;使用栈来模拟递归。 文字有点简略&#xff0c;需要看图和代码理解 树节点&#xff1a; typedef char DATA; //树节点 typedef struct Node {DATA data; //数据struct Node* left…
阅读更多...
MySQL进阶-----Linux系统安装MySQL

MySQL进阶-----Linux系统安装MySQL

目录 前言 一、准备工作 1. 准备一台Linux服务器 2. 下载Linux版MySQL安装包 3. 上传MySQL安装包 二、安装操作指令 1. 创建目录,并解压 2.安装mysql的安装包 三、开启mysql与密码修改 1.启动MySQL服务 2. 查询自动生成的root用户密码 3.修改root用户密码 四、创…
阅读更多...
【LeetCode】升级打怪之路 Day 26：回溯算法 — 集合划分问题

【LeetCode】升级打怪之路 Day 26：回溯算法 — 集合划分问题

今日题目&#xff1a; 698. 划分为k个相等的子集 | LeetCode473. 火柴拼正方形 | LeetCode 参考文章&#xff1a; 经典回溯算法&#xff1a;集合划分问题 目录 LC 698. 划分为k个相等的子集 【classic&#xff0c;有难度】数据预处理&#xff1a;计算 target基本回溯优化 1&…
阅读更多...
限时免费！Unity 资源商店威尔房间精品资源等你来领！

限时免费！Unity 资源商店威尔房间精品资源等你来领！

Unity 资源商店威尔房间精品资源分享 资源介绍资源特色免费领取 Unity 商店资源&#xff1a;Will’s Room Environment, Dormitory Room Environment 免费获取。 资源介绍 好消息来啦&#xff01;Unity 资源商店的威尔房间精品资源正在限时免费中&#xff01;这是一个非常受欢迎…
阅读更多...
一维前缀和一维差分（下篇讲解二维前缀和二维差分）（超详细，python版，其他语言也很轻松能看懂）

一维前缀和一维差分（下篇讲解二维前缀和二维差分）（超详细，python版，其他语言也很轻松能看懂）

本篇博客讲解一维前缀和&#xff0c;一维差分&#xff0c;还会给出一维差分的模板题&#xff0c;下篇博客讲解 二维前缀和&二维差分。 一维前缀和&#xff1a; 接触过算法的小伙伴应该都了解前缀和&#xff0c;前缀和在算法中应用很广&#xff0c;不了解也没有关系&#…
阅读更多...
【算法】小强爱数学（迭代公式+数论取模）

【算法】小强爱数学（迭代公式+数论取模）

文章目录 1. 问题2. 输入3. 输出4. 示例5. 分析6. 思路7. 数论&#xff0c;取模相关公式8. 数论&#xff0c;同余定理9. 代码 1. 问题 小强发现当已知 x y B xyB xyB以及 x y A xyA xyA时,能很轻易的算出 x n x_ {n} xn​ y n y_ {n} yn​ 的值.但小强想请你在已知A和B的…
阅读更多...
【No.16】蓝桥杯动态规划下|线性DP装箱问题|计数DP0/1背包的方案数|过河卒|完全背包小明的背包2|最长公共子序列|蓝桥骑士|推荐练习题(C++)

【No.16】蓝桥杯动态规划下|线性DP装箱问题|计数DP0/1背包的方案数|过河卒|完全背包小明的背包2|最长公共子序列|蓝桥骑士|推荐练习题(C++)

线性DP&#xff0c;0/1背包简化版&#xff0c;装箱问题 【题目描述】有一个箱子容量为V(正整数&#xff0c; 0 ≤ V ≤ 20000 0 \le V \le 20000 0≤V≤20000)&#xff0c;同时有n个物品( 0 < n ≤ 30 0 < n \le 30 0<n≤30)&#xff0c;每个物品有一个体积(正整数)。…
阅读更多...
ubuntu20.04安裝輸入法

ubuntu20.04安裝輸入法

文章目录 前言一、操作過程1、安装fcitx-googlepinyin2、配置language support 前言 參考文獻 一、操作過程 1、安装fcitx-googlepinyin sudo apt-get install fcitx-googlepinyin2、配置language support 第一次點擊進去&#xff0c;會讓你安裝 點擊ctrl和空格切換中英文…
阅读更多...
Gin入门指南：从零开始快速掌握Go Web框架Gin

Gin入门指南：从零开始快速掌握Go Web框架Gin

官网：https://gin-gonic.com/ GitHub：https://github.com/gin-gonic 了解 Gin Gin 是一个使用 Go 语言开发的 Web 框架，它非常轻量级且具有高性能。Gin 提供了快速构建 Web 应用程序所需的基本功能和丰富的中间件支持。 以下是 Gin 框架的一些特点和功能： 快速而高效：…
阅读更多...
000_coolprop_in_matlab在Matlab中使用CoolProp

000_coolprop_in_matlab在Matlab中使用CoolProp

在Matlab中使用CoolProp 简介 CoolProp是一个开源的热力学性质库&#xff0c;可以计算多种流体的热力学性质。CoolProp支持多种编程语言&#xff0c;包括Python、C、Matlab等。本文将介绍如何在Matlab中使用CoolProp。 CoolProp官网 本文所使用的Matlab版本为R2021a。 在Ma…
阅读更多...
Zabbix与Prometheus区别简述

Zabbix与Prometheus区别简述

Zabbix与Prometheus区别简述 历史沿革 一、监控工具简介 1、Zabbix https://www.zabbix.com/cn/download Zabbix是传统的监控系统&#xff0c;出现比云原生早&#xff0c;使用的是SQL关系型数据库&#xff1b;开源监控软件&#xff0c;遵守 GPLv2开源协议&#xff0c;起源于…
阅读更多...
为什么说 C/C++ 不适合做 Web 开发？

为什么说 C/C++ 不适合做 Web 开发？

Web开发是当今信息技术领域的重要组成部分&#xff0c;涉及创建、维护和优化供浏览器访问的网站和应用程序。在众多编程语言中&#xff0c;C/C因其高效、灵活和接近硬件的特性而备受推崇&#xff0c;但在Web开发领域&#xff0c;它们并不被视为首选工具。本文将从以下几个方面探…
阅读更多...
Linux Sftp和Scp

Linux Sftp和Scp

scp 和 sftp 区别 1 scp 能将远程文件复制到另一个远程机&#xff0c;sftp 不能。sftp为 SSH的其中一部分&#xff0c;是一种传输档案至 Blogger 伺服器的安全方式 2.scp 没有删除/创建远程目录功能&#xff0c;sftp 有。scp 在需要进行验证时会要求你输入密码或口令。 3. FT…
阅读更多...
【算法】回溯与深搜

【算法】回溯与深搜

方法论 1.构建决策树 2.设计代码&#xff1a;全局变量、dfs函数 3.剪枝&#xff0c;回溯 全排列 给定一个不含重复数字的整数数组 nums &#xff0c;返回其 所有可能的全排列 。可以 按任意顺序 返回答案。 示例 1&#xff1a; 输入&#xff1a;nums [1,2,3] 输出&#xff…
阅读更多...
力扣---随机链表的复制

力扣---随机链表的复制

给你一个长度为 n 的链表&#xff0c;每个节点包含一个额外增加的随机指针 random &#xff0c;该指针可以指向链表中的任何节点或空节点。 构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成&#xff0c;其中每个新节点的值都设为其对应的原节点的值。新节点的 n…
阅读更多...
进程和线程的关系与区别

进程和线程的关系与区别

目录&#xff1a; 导言&#xff1a; 正文&#xff1a; 一.进程 1.概念 2.进程控制块&#xff08;Process Control Block&#xff0c;PCB) 3.状态 4.优缺点 二.线程 1.概念 2.线程的设计理由与优点 3.缺点 三.进程与线程的区别与联系 导言&#xff1a; 在现代计算机…
阅读更多...
ctf__

ctf__

title: ctf 2.题目类别 3.题目的细分 4.例题 misc 0x05. 明文攻击 明文攻击是一种较为高效的攻击手段&#xff0c;大致原理是当你不知道一个zip的密码&#xff0c;但是你有zip中的一个已知文件&#xff08;文件大小要大于12Byte&#xff09;时&#xff0c;因为同一个zip压缩…
阅读更多...
java数据结构与算法刷题-----LeetCode215. 数组中的第K个最大元素

java数据结构与算法刷题-----LeetCode215. 数组中的第K个最大元素

java数据结构与算法刷题目录&#xff08;剑指Offer、LeetCode、ACM&#xff09;-----主目录-----持续更新(进不去说明我没写完)&#xff1a;https://blog.csdn.net/grd_java/article/details/123063846 文章目录 解题思路&#xff1a;时间复杂度O( n n n)&#xff0c;空间复杂度…
阅读更多...
大屏可视化综合展示解决方案

大屏可视化综合展示解决方案

1.系统概述 1.1.需求分析 1.2.重难点分析 1.3.重难点解决措施 2.系统架构设计 2.1.系统架构图 2.2.关键技术 2.3.接口及要求 3.系统功能设计 3.1.功能清单列表 3.2.数据源管理 3.3.数据集管理 3.4.视图管理 3.5.仪表盘管理 3.6.移动端设计 3.1.系统权限设计 3.…
阅读更多...
STM32 CAN的位时序和波特率

STM32 CAN的位时序和波特率

STM32 CAN的位时序和波特率 位时序 STM32的CAN外设位时序中只包含3段&#xff0c;分别是同步段SYNC_SEG、位段BS1及位段BS2&#xff0c;采样点位于BS1及BS2段的交界处。其中SYNC_SEG段固定长度为1Tq&#xff0c;而BS1及BS2段可以在位时序寄存器CAN_BTR设置它们的时间长度&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023