---

前言

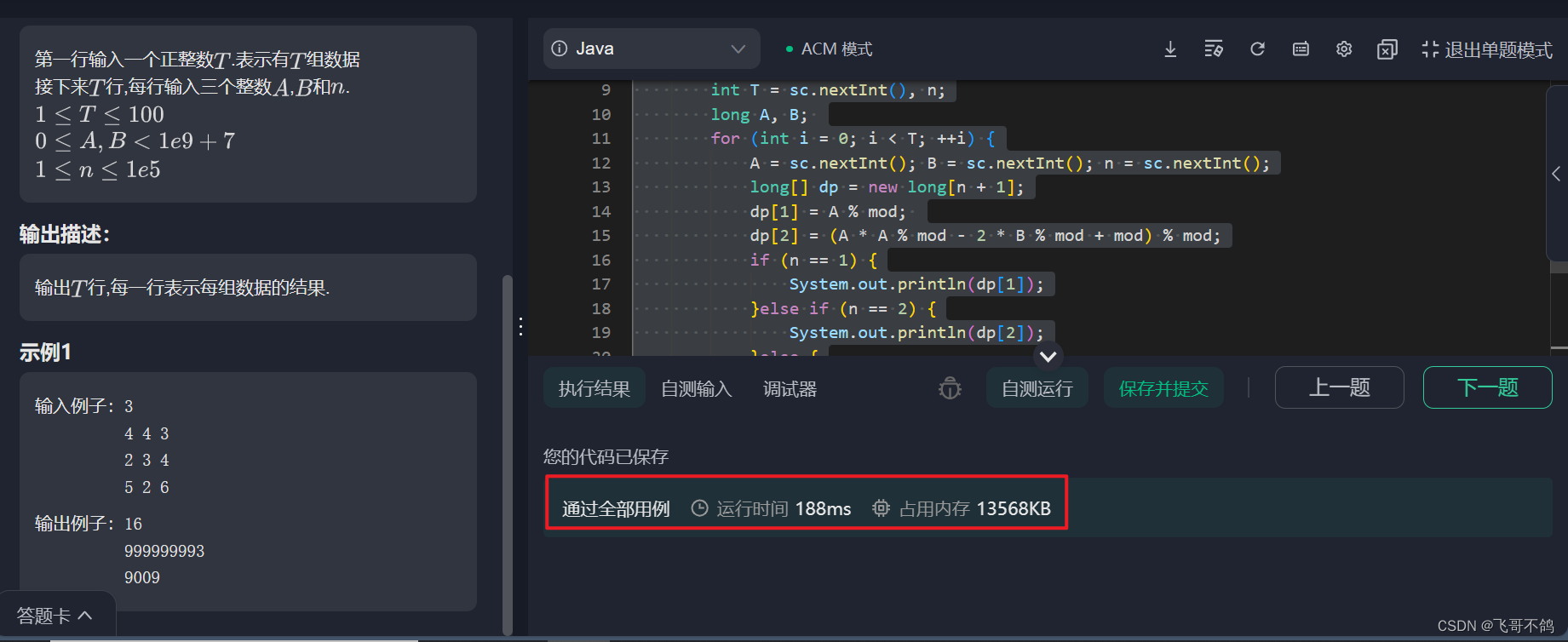
本文实现二叉树的前中后的非递归遍历，使用栈来模拟递归。
文字有点简略，需要看图和代码理解

树节点：

typedef char DATA;
//树节点
typedef struct Node
{
	DATA data;	//数据
	struct Node* left;	//左子树
	struct Node* right;	//右子树
	bool ok;	//判断完成左子树遍历 ，用于后序遍历
	Node(DATA d)
	{ data = d;
	left = right = NULL;
	ok = true;
	}
}Node;

手搓树：

/构建树
void Tree::Achievements()
{
	Node*  p1 = new Node('a');

	Node* p2 = new Node('b');

	Node* p3 = new Node('c');

	Node* p4 = new Node('d');

	Node* p5 = new Node('e');


	p1->left = p2;
	p1->right = p3;
	p2->right = p4;
	p3->left = p5;

	this->root = p1;
}

一、前序

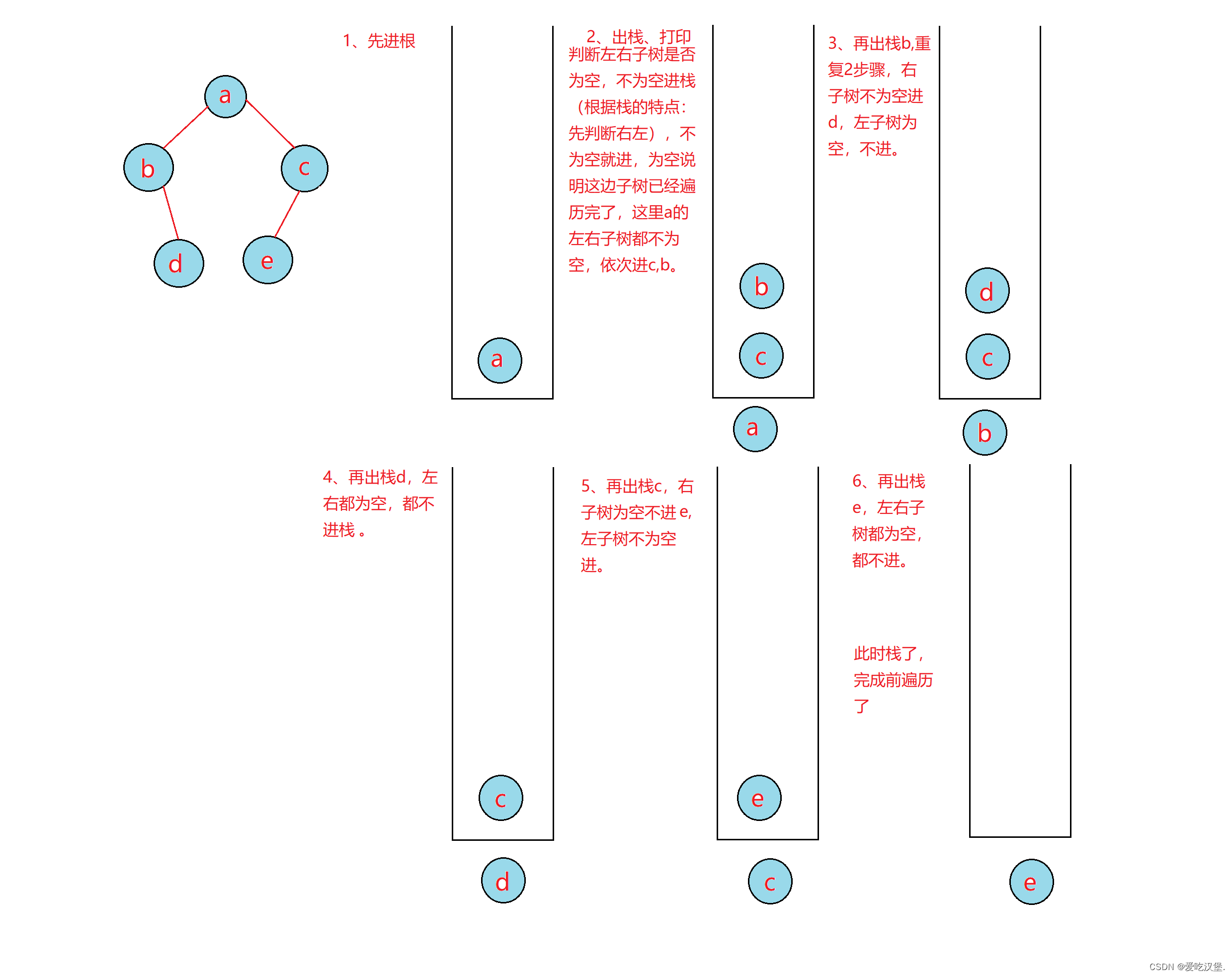
前序遍历：先根后左右子树
我们通过栈来模拟递归过程：
根据栈的特点：先进先出，所以我们先然右子树进栈再让左子树进栈，这样就符合前序遍历了
代码实现：

//前序遍历 ： 根 -> 左子树 -> 右子树
void Tree::Preamble()
{
	//利用栈实现
	stack<Node*> sta;
	//判断是否为空
	if (this->root == NULL)
	{
		return;
	}
	//根先入栈
	sta.push(this->root);

	//当栈空时说明已经遍历完了
	while (!sta.empty())
	{
		//取栈顶元素并出栈
		Node* tmp = sta.top();
		sta.pop();
		cout << tmp->data << "->";

		//因为栈的特点：先进先出，所以先压右子树，在压左子树，这样就可以做到先左子树了
		if (tmp->right != NULL)
		{
			sta.push(tmp->right);
		}
		if (tmp->left != NULL)
		{
			sta.push(tmp->left);
		}
	}
}

运行结果：

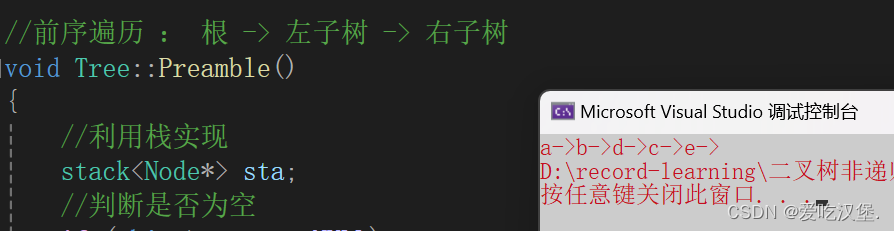
图解：

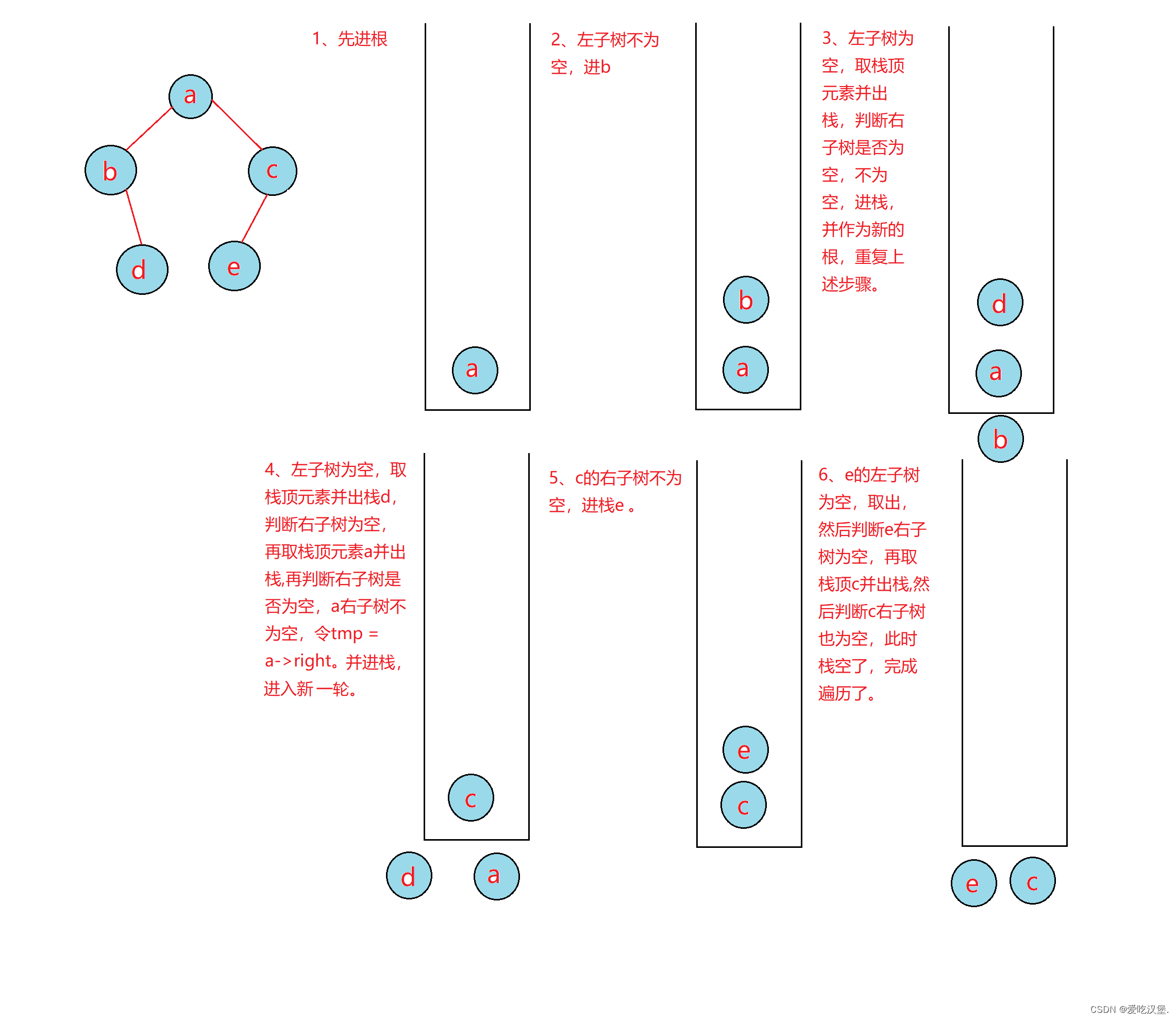
二、中序

中序遍历：先左子树再根最后右子树
依旧用模拟栈来实现：先让左子树先出完再出根再右子树
代码实现：

//中序遍历 :先左子树，再根，最后右子树
void Tree::MediumOrder()
{
	//判断是否为空
	if (this->root == NULL)
	{
		return;
	}
	//栈
	stack<Node*> sta;
	//先进根
	sta.push(this->root);
	Node* tmp = this->root;

	//出循环条件
	while (!sta.empty()&&tmp!=NULL)
	{
		//左不为空就进左
		if (tmp->left != NULL)
		{
			sta.push(tmp->left);
			tmp = tmp->left;
		}
		//直到左为空了，开始出栈
		else if (tmp->left == NULL)
		{
			//取栈顶并出栈
			tmp = sta.top();			
			sta.pop();
			cout << tmp->data << "->";

			//右子树为空就说明这个子树遍历完了，可以回到上一级根了（栈顶元素），再判断其右子树是否为空
			while (!sta.empty()&&tmp->right == NULL)
			{
				tmp = sta.top();
				cout << tmp->data << "->";
				sta.pop();
			}
			//右子树不为空进栈，并作为新的根，再往下走
				sta.push(tmp->right);
				tmp = tmp->right;
		}
	}
}

运行结果：

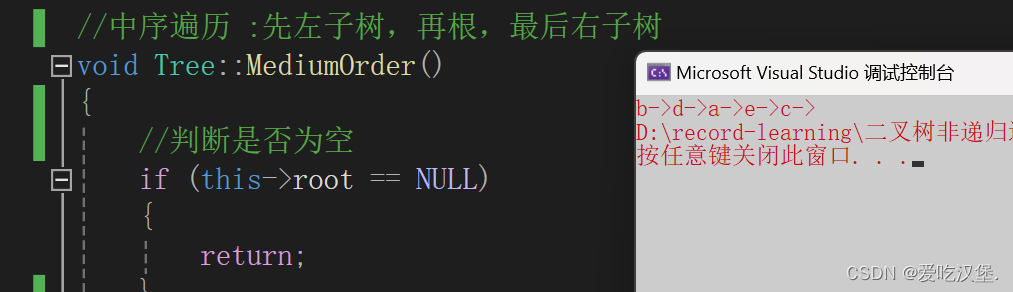
图解：

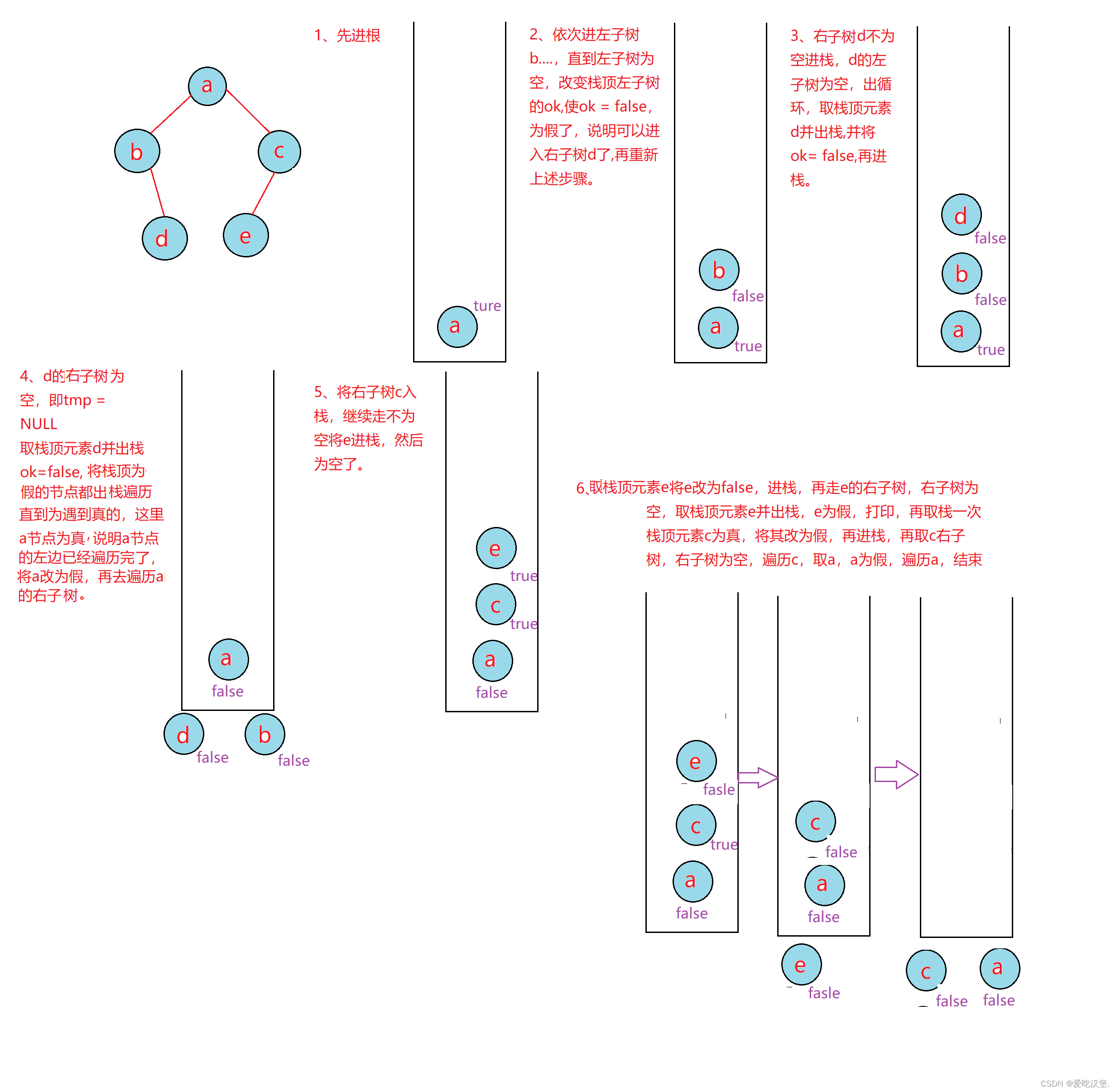
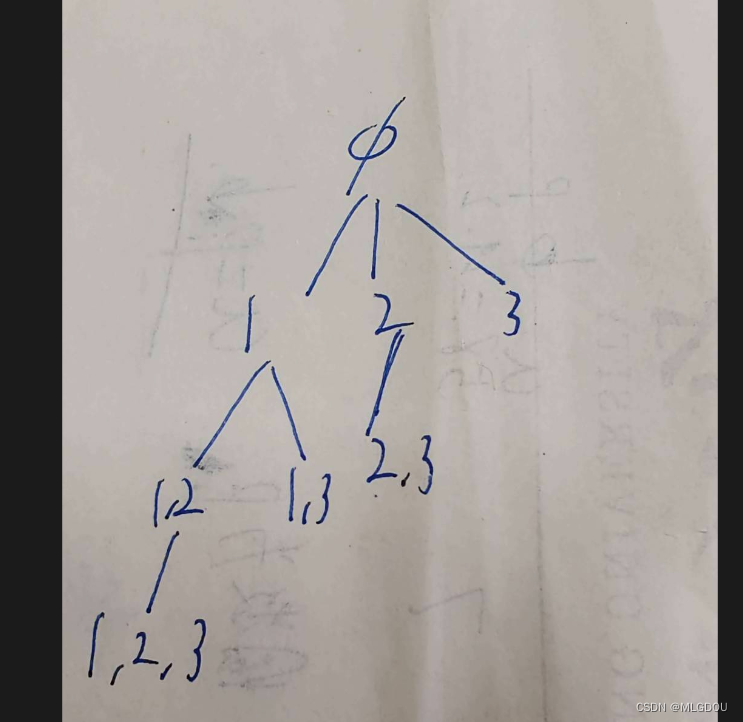
三、后序

后序：先左子树再右子树最后根
还是用栈来模拟，但是在树节点加了一个bool变量来判断是否走完左子树了，判断为假的话就该走右子树了。

代码实现：

后序遍历：左子树再右子树最后根
void Tree::Postscript()
{
	//判断是否为空
	if (this->root == NULL)
	{
		return;
	}
	//栈
	stack<Node*> sta;
	//先让根入栈
	Node* tmp = this->root;
	sta.push(tmp);
	
	//从根的左节点开始
	tmp = tmp->left;

	while (!sta.empty() || tmp != NULL)
	{
		//不为空就继续进栈，直到为空
		while (tmp != NULL)
		{
			sta.push(tmp);
			tmp = tmp->left;
		}

		//左子树为空，取栈顶元素并出栈
		tmp = sta.top();
		sta.pop();

		//判断为真改变为假再入栈
		if (tmp->ok)
		{
			tmp->ok = false;
			sta.push(tmp);
			//栈顶元素为ok假了，该走右了
			tmp = tmp->right;
		}
		//假，将栈顶往下为假的元素都出，直到为真的再重新走
		else
		{   
			cout << tmp->data << "->";
			//遍历到根节点了
			if (tmp == this->root)
			{
				return;
			}
			else
				tmp = NULL;
		}
	}
	}

运行结果：

图解：