方法论

1.构建决策树
2.设计代码：全局变量、dfs函数
3.剪枝，回溯

全排列

给定一个不含重复数字的整数数组 nums ，返回其 所有可能的全排列 。可以 按任意顺序 返回答案。
示例 1：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：
输入：nums = [0,1]
输出：[[0,1],[1,0]]

思路：

首先构建决策树，这道题无非就是遍历所有数字然后组合，我们选择采用dfs深度优先的遍历方法，同时用一个bool数组check判断该数是否被遍历过，每一遍的答案放在path数组里，当path数组的长度等于nums长度时则加入到ret结果数组中，同时回溯，即把path数组pop_back(),并把check数组的该位置设为false。

class Solution {
    vector<vector<int>> ret;
    vector<int> path;
    bool check[7];
public:
    vector<vector<int>> permute(vector<int>& nums) 
    {
        dfs(nums);
        return ret;
    }

    void dfs(vector<int>& nums)
    {
        if(nums.size()==path.size())
        {
            ret.push_back(path);
            return;
        }

        for(int i=0;i<nums.size();i++)
        {
            if(check[i]==false)
            {
                path.push_back(nums[i]);
                check[i]=true;
                dfs(nums);
                //回溯（恢复现场）
                path.pop_back();
                check[i]=false;
            }
        }
    }
};

子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的
子集
（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2：

输入：nums = [0]
输出：[[],[0]]

思路1：

从0到n遍历nums，决策树判断每个元素选不选

class Solution {
    vector<vector<int>> ret;
    vector<int> path;
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(nums,0);
        return ret;
    }

    void dfs(vector<int>& nums,int pos)
    {
        if(pos==nums.size())
        {
            ret.push_back(path);
            return;
        }

        //选
        path.push_back(nums[pos]);
        dfs(nums,pos+1);
        path.pop_back();//恢复现场

        //不选
        dfs(nums,pos+1);
        
    }
};

思路2：

构建决策树以节点数量来判断，第一层为空，第二层一个节点，第三层两个节点，以此类推。

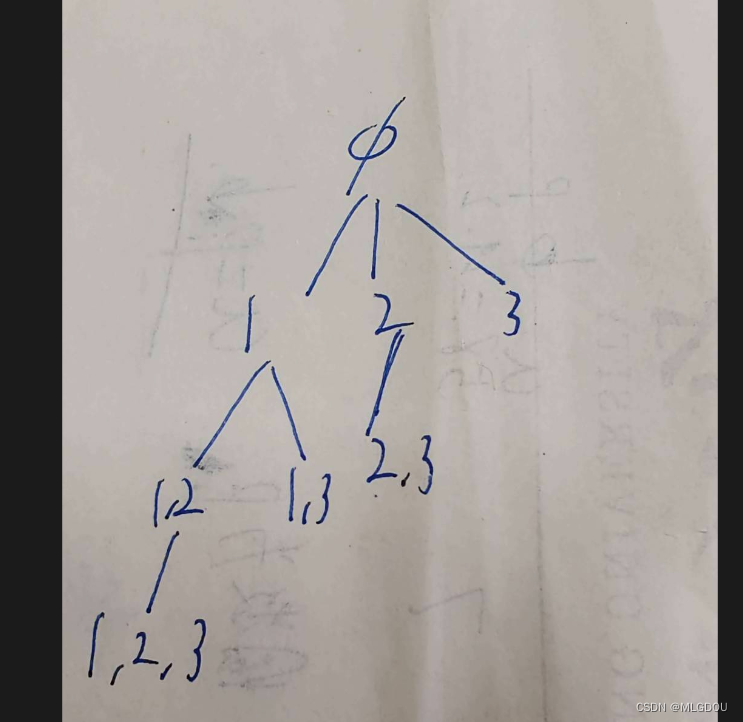
class Solution {
    vector<int> path;
    vector<vector<int>> ret;
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(nums,0);
        return ret;
    }

    void dfs(vector<int>& nums,int pos)
    {
        ret.push_back(path);

        for(int i=pos;i<nums.size();i++)
        {
            path.push_back(nums[i]);
            dfs(nums,i+1);
            path.pop_back();
        }
    }
};