【LeetCode】升级打怪之路 Day 26：回溯算法

【LeetCode】升级打怪之路 Day 26：回溯算法 — 集合划分问题

news2024/11/14 8:31:27

今日题目：

698. 划分为k个相等的子集 | LeetCode
473. 火柴拼正方形 | LeetCode

参考文章：

经典回溯算法：集合划分问题

LC 698. 划分为k个相等的子集【classic，有难度】

698. 划分为k个相等的子集 | LeetCode

我们可以理解为有 k 个桶，我们需要尝试将各个数字分别放入所有桶中，使得每个桶的 sum 都相等。

基本思路就是采用回溯算法，在“做选择”这一步，就是将一个数字分别选择放入各个不同的桶中，这样回溯决策树的第 i 层就是决定将 nums[i] 放入哪个 bucket 中。

但这种基本的回溯就等同于暴力搜索了，在 LeetCode 中提交后会出现超时错误，解决方法就是优化某些步骤，尽可能地剪枝。

数据预处理：计算 target

这一步很重要。因为我们是让每个 bucket 中的 sum 都相等，那自然每个 bucket 的 sum 就等于 所有数字的加和 / bucket 数量，所以我们先计算出 target，也就是最终每个 bucket 中的所有数字的累加需要达到的目标。

int sum = Arrays.stream(sum).sum();
// 如果 sum 不能平分，则直接可以判定找不到答案
if (sum % k != 0) {
	return false;
}
int target = sum / k;  // 每个 bucket 的累加需要达到的目标

通过上面我们计算出了 target，就可以在回溯时提前判断当 bucket 的数字累加超过了 target 时，就可以提前剪枝了。

基本回溯

由此，我们可以写出如下的解决代码：

class Solution {

    private boolean backtrack(int[] buckets, int target, int[] nums, int k, int level) {
        if (level >= nums.length) {
            for (int bucket: buckets) {
                if (bucket != target) {
                    return false;
                }
            }
            return true;
        }

        int num = nums[level];
        for (int i = 0; i < k; i++) {  // 遍历各个 bucket
            int sum = buckets[i] + num;  // 如果做出选择后，这个 bucket 的累加和
            if (sum > target) {  // 如果超出了 target，就提前剪枝
                continue;
            }
            buckets[i] = sum;
            boolean ok = backtrack(buckets, target, nums, k, level + 1);
            if (ok) {
                return true;
            }
            buckets[i] -= num;
        }

        return false;
    }

    public boolean canPartitionKSubsets(int[] nums, int k) {
        int sum = Arrays.stream(nums).sum();
        if (sum % k != 0) {
            return false;
        }
        int target = sum / k;
        int[] buckets = new int[k];
        Arrays.fill(buckets, 0);
        return backtrack(buckets, target, nums, k, 0);
    }
}

这个思路是没问题了，但是很遗憾，还是复杂度过高，超时。

优化 1：跳过某些 bucket 的选择

这里存在一个重要优化：当你做选择想把某个 num 放入一个 bucket 时，如果这个 bucket 的累加和与上一个 bucket 的累加和相同，那把这个 num 放入当前这个 bucket 的结果与放入上一个 bucket 的结果是一样的，上一个选择没有让我们找出答案，那这一次选择也不会让我们找出答案，因此可以直接剪枝跳过。

由此，在上面的代码中，我们可以加入这样一个优化：

这个优化只需要让我们加一个小判断，就能剪掉很多枝。

优化 2：事先对 nums 排序

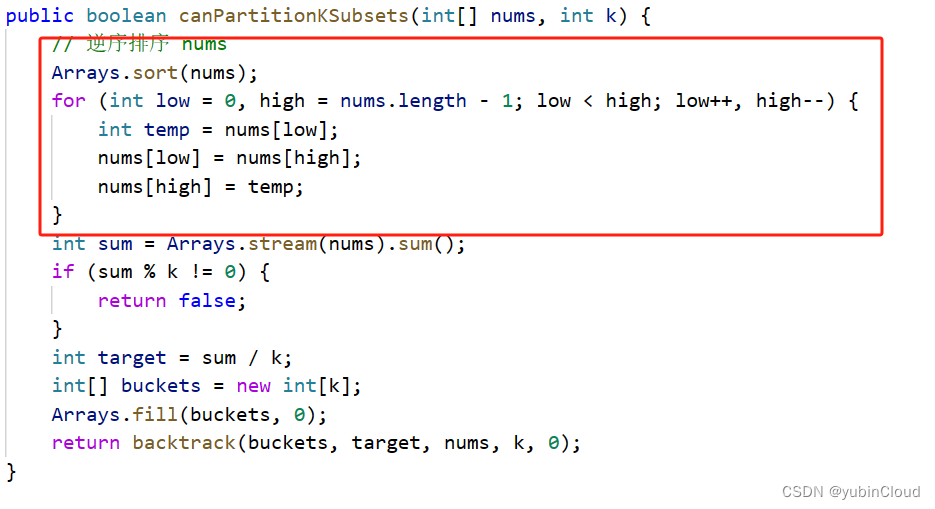
因为我们会判断当前 bucket 的和是否超过了 target 进而剪枝，那事先对 nums 逆序排序，将大的数字放在前面，就更快地出现剪枝，从而减小复杂度。所以，我们可以在一开始先对 nums 进行逆序排序：

逆序排序

最终代码事先

在基本的回溯代码再加上上面两个优化后，就可以通过 LeetCode 的检测了。最终代码如下：

class Solution {

    private boolean backtrack(int[] buckets, int target, int[] nums, int k, int level) {
        if (level >= nums.length) {
            for (int bucket: buckets) {
                if (bucket != target) {
                    return false;
                }
            }
            return true;
        }

        int num = nums[level];
        // 遍历各个 bucket 做选择
        for (int i = 0; i < k; i++) {
            // 如果当前桶和上一个桶内的元素和相等，则跳过
            // 原因：如果元素和相等，那么 nums[index] 选择上一个桶和选择当前桶可以得到的结果是一致的
            if (i != 0 && buckets[i] == buckets[i - 1]) {
                continue;
            }
            int sum = buckets[i] + num;  // 如果做出选择后，这个 bucket 的累加和
            if (sum > target) {   // 如果超出了 target，就提前剪枝
                continue;
            }
            buckets[i] = sum;
            boolean ok = backtrack(buckets, target, nums, k, level + 1);
            if (ok) {
                return true;
            }
            buckets[i] -= num;
        }

        return false;
    }

    public boolean canPartitionKSubsets(int[] nums, int k) {
        // 逆序排序 nums
        Arrays.sort(nums);
        for (int low = 0, high = nums.length - 1; low < high; low++, high--) {
            int temp = nums[low];
            nums[low] = nums[high];
            nums[high] = temp;
        }
        int sum = Arrays.stream(nums).sum();
        if (sum % k != 0) {
            return false;
        }
        int target = sum / k;
        int[] buckets = new int[k];
        Arrays.fill(buckets, 0);
        return backtrack(buckets, target, nums, k, 0);
    }
}