1 浮点数的不精确性

能不能用二进制表示所有实数，然后在二进制下计算它的加减乘除呢？

打开Chrome Console，输入0.3 + 0.6：

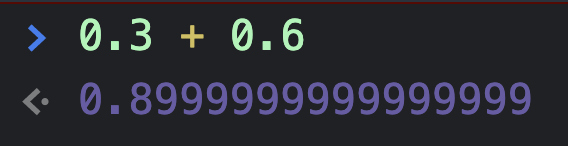
简单加法在js算出结果居然不是准确的0.9，而是0.8999999999999999，why？

计算机通常用16/32比特（bit）表示一个数。32比特能表示所有实数吗？显然不。32个比特，只能表示2^32=40亿。超过这数，就会有两个不同的数的二进制表示相同 。计算机就不知道这个数到底是啥。

40亿个数看起来很多，但比起无限多的实数集合也就渺小。到底应该让这40亿个数映射到实数集合上的哪些数，在实际应用中才最划得来？

2 定点数

直观的，4比特表示0～9整数，则32比特即可表示8个这样的整数：

• 然后把最右边的2个0～9的整数，当成小数部分
• 左边6个0～9的整数，当成整数部分

就可用32比特表示从0~999999.99这样1亿个实数。

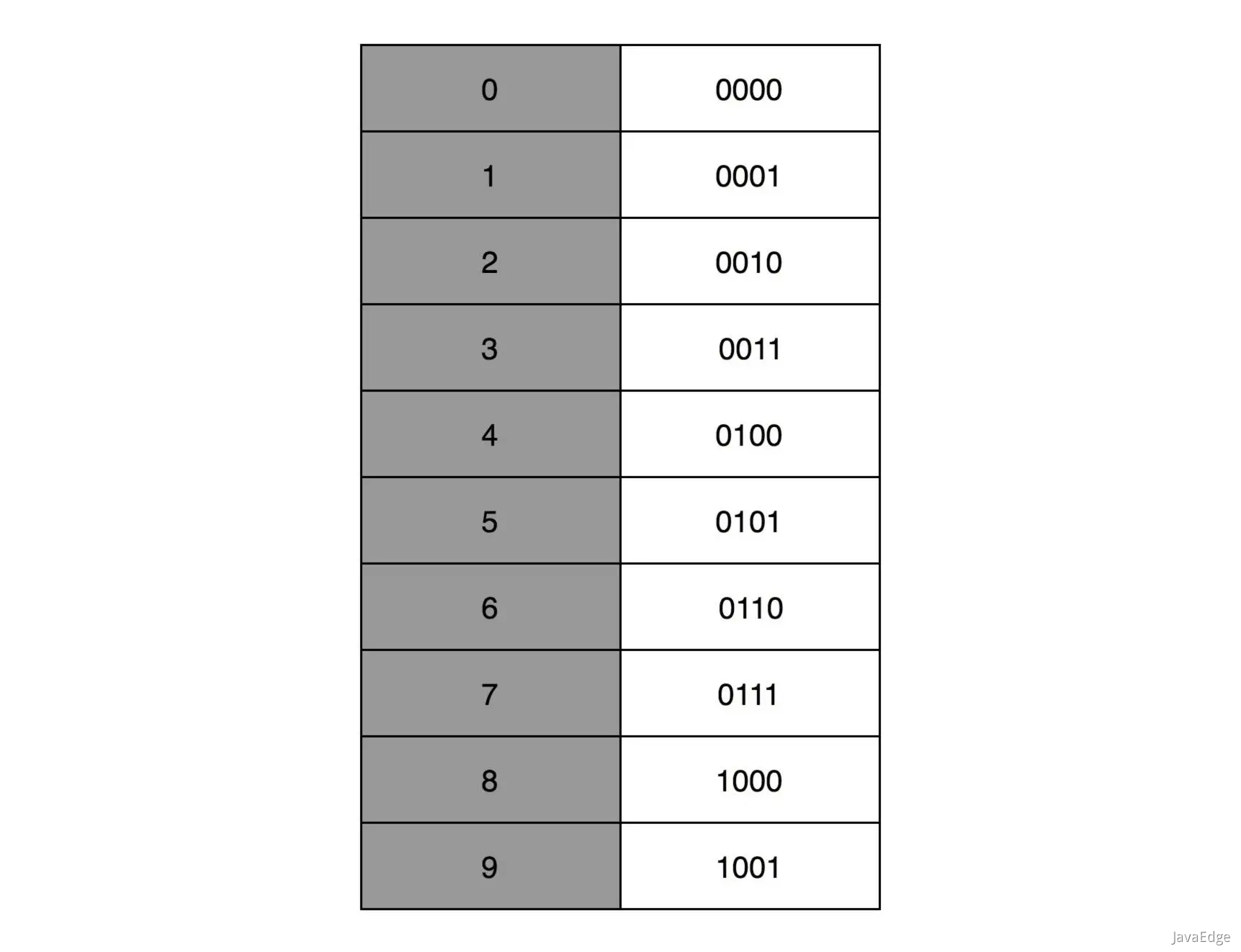
这种二进制表示十进制的编码方式，叫BCD编码（Binary-Coded Decimal)。最常用的是在超市、银行这样需要用小数记录金额的情况里。超市小数最多到分。这样的表示方式，直观清楚，满足小数部分计算。

3 缺点

• 浪费
  本来32比特可表示40亿个不同数，但BCD编码只能表示1亿个数，要精确到分，那么能够表示的最大金额也就是到100万。
  货币单位是人民币或者美元还好，津巴布韦币数量就不够。
• 无法同时表示很大数和很小数
  有时想表示商品金额，关心9.99这样小数字；有时候，物理学运算，需要表示光速，即 $3\times 10^8$ 这样大数。
  是否既能够表示很小的数，又能表示很大数？

4 浮点数（Floating Point）

即float类型。在一张便签纸上，用一行来写一个十进制数，能够写下多大范围的数？
要让人能够看清楚，所以字最小也有一个限制：纸张宽度限制了能表示的数大小。如宽度只放下8个数，还是只能写下最大到99999999这样的数字。

这纸张宽度和32比特一样，在空间层限制。现实怎么表示大数？如宇宙内原子数量，莫非是用一页纸，用好多行写下很多0？不，我们用科学计数法，如 1.0×10^82，而非写82个0。
计算机也可采用类似办法，用科学计数法表示实数。浮点数科学计数法有个IEEE标准，定义两个基本格式：

• 32比特表示单精度浮点数，即float或float32类型
• 64比特表示双精度浮点数，即double或float64类型
  
  单精度的32比特可分成三部分。
• 第一部分，一个符号位，表示正数or负数。s表示。浮点数不像正数，分符号数还是无符号数，所有浮点数都是有符号。
• 8比特组成指数位。e表示。8比特能表示的整数空间：0～255。这里用1～254映射到-126～127这254个有正有负的数上。
  浮点数，不仅想要表示大数，还希望能够表示很小的数，所以指数位也有负数。
  没有用到0和255。没错，这里的 0（也就是8个比特全部为0） 和 255 （也就是8个比特全部为1）另有它用。
• 23比特组成的有效数位。用f来表示

科学计数法的浮点数表示：
$(-1{)}^s\times 1.f\times 2^e$

这里的浮点数，无法表示0。要表示0和一些特殊数，就要用上在e里留下的0和255，这两个其实是标记位。
e=0 f=0时，就把这个浮点数认为是0：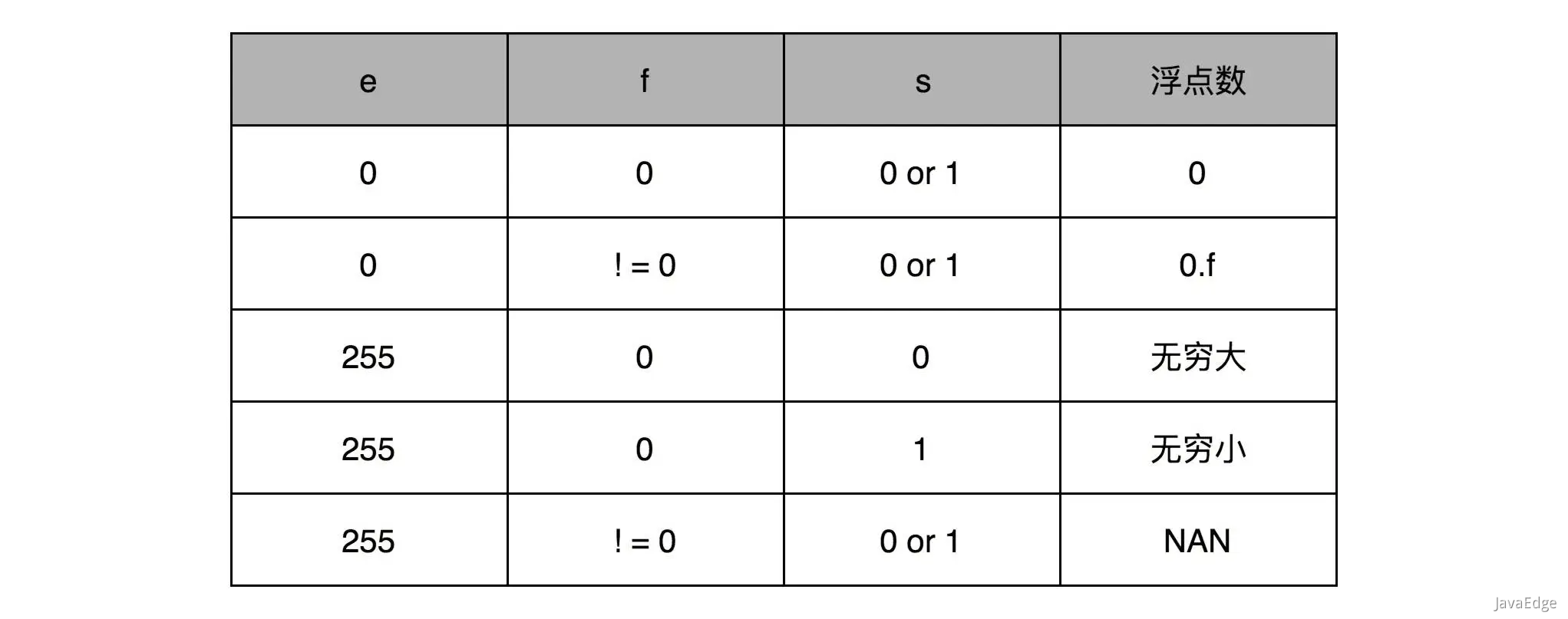
如0.5的符号s应该是0，f应该是0，而e应该是-1，也就是

$0.5=(-1{)}^0\times 1.0\times 2^{-1}=0.5$，对应的浮点数表示，就是32个比特。

$s=0，e=2^{-1}$，需要注意，e表示从-126到127个，-1是其中的第126个数，这里的e如果用整数表示，就是$2^6+2^5+2^4+2^3+2^2+2^1=126$，$1.f=1.0$。

这样的浮点数表示下，不考虑符号，浮点数能表示的最小数和最大数：
$1.17\times 10^{-38}$
$3.40\times 10^{38}$

比前面的BCD编码能够表示的范围大多了。

5 总结

这样的表示方式下，浮点数能够表示的数据范围一下子大了很多。
因为这个数对应的小数点的位置“浮动”，才被称为浮点数。随指数位e值不同，小数点位置也在动。
对应的，前面的BCD编码的实数，就是小数点固定在某一位的方式，我们也就把它称为定点数。

为什么0.3 + 0.6不能得到0.9？
因为，浮点数没有办法精确表示0.3、0.6和0.9。0.1～0.9这9个数，只有0.5能够被精确地表示成二进制的浮点数：s = 0、e = -1、f = 0。

而0.3、0.6、0.9，都只是近似表达。浮点数无论是表示还是计算其实都是近似计算。