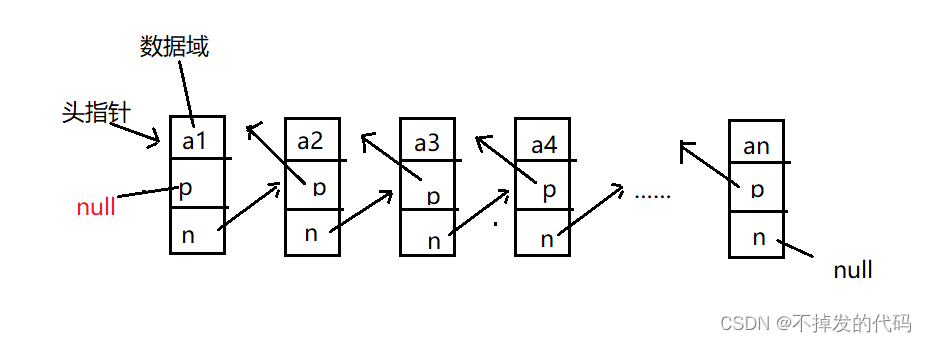
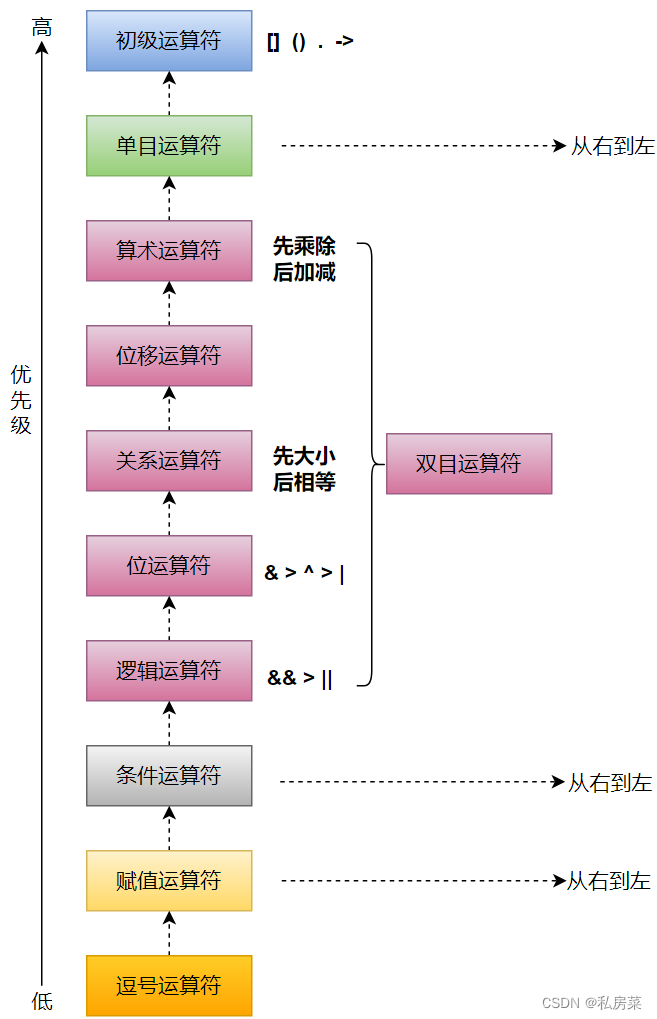
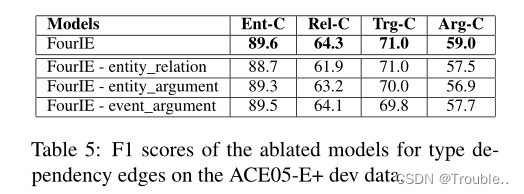
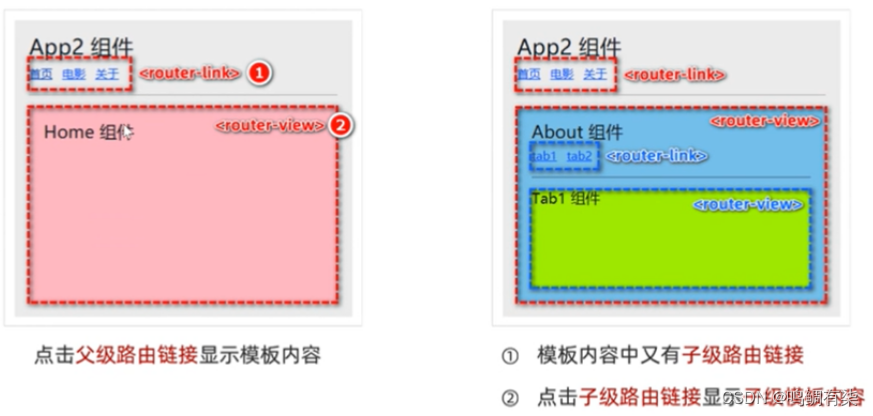
Node Embeddings
- 一、Graph Representation Learning
- 二、Node Embeddings:Encoder and Decoder
- 三、Random Walk Approaches for Node Embeddings
一、Graph Representation Learning
在传统的图机器学习中,依赖于手工特征工程(即由特征工程师去设计节点、边、图的features);给定一个输入图,依靠人工去提取节点、链接和图级特征,学习将特征映射到标签的模型(SVM、神经网络等)。流程表示如下图:

为了去掉手工特征工程这一步,提出了图表示学习(Graph Representation Learning);换句话说:图表示学习移除了每次都进行特征工程的需要。

Graph Representation Learning的目标:
输入一张图
G
G
G,能够学习一个函数
f
f
f将节点
v
v
v映射到一个
d
d
d维的空间。即将图
G
G
G嵌入到一个
d
d
d维空间。

这个映射后的 d d d维向量称为feature representation或embedding。
Embedding的任务:
将节点映射到embedding space中,即将节点统一映射到一个
d
d
d维空间。
-
嵌入后,在 d d d维空间中节点间的相似性能够表示节点在图中的相似性。
- 如:将一个简单网络映射到二维空间中,在二维空间中相同类的节点在距离上是比较接近的。

- 如:将一个简单网络映射到二维空间中,在二维空间中相同类的节点在距离上是比较接近的。
-
可以使用Encode network来实现映射
-
映射后的 d d d维向量可以直接用于下游任务的预测
- 第一小节主要讲的是,希望能够避免人工的去设计feature,而是由模型自动完成。所以提出了Graph Representation Learning,任务是输入一张图的信息,如邻接矩阵,然后通过模型(编码器)将图 G G G的节点映射到一个新的空间,在使用这个节点在新空间所代表的向量来实现实际的任务。
- 上述内容不理解,可以先看一下吴恩达老师的词嵌入视频,都是类似的。【笔记指路】
二、Node Embeddings:Encoder and Decoder
假设我们有一张图 G G G:
- V V V是顶点集
- A A A是邻接矩阵

节点嵌入的目标:
对节点进行编码,以便嵌入空间中的相似性接近图中的相似性;
如下图,在图上的相似度在新的嵌入空间中也能够体现。

在embedding space上的相似度可以使用向量的内积来表示,所以我们的目标可写成:
s
i
m
i
l
a
r
i
t
y
(
u
,
v
)
≈
z
v
T
z
u
similarity(u,v)≈z_v^Tz_u
similarity(u,v)≈zvTzu

为什么内积可作为新空间的相似度度量?(个人见解)
每个节点都在新空间上都由一个 d d d维的向量表示,向量的每个原始都表示节点的一个属性,该属性越明显,则该值就越大。若两个节点之间都具有这个属性,那么内积的结果就会越大。(类似CNN的卷积)
学习节点嵌入的方法:
- 训练一个编码器(Encoder,ENC)将节点映射到embedding space
- 定义一个节点相似度函数(即原始网络中相似度的度量)
- 训练一个解码器(Decoder,DEC)将embeddings映射为相似度得分
- 优化编码器的参数,使:
s i m i l a r i t y ( u , v ) ≈ z v T z u similarity(u,v)≈z_v^Tz_u similarity(u,v)≈zvTzu
个人理解:
内积可能不是能够很好的表示两个节点在新空间的相似度,所以训练了一个解码器用于输出两节点在新空间的相似性,上式可写成:
s i m i l a r i t y ( u , v ) ≈ D E C ( z v T z u ) similarity(u,v)≈DEC(z_v^Tz_u) similarity(u,v)≈DEC(zvTzu)
实际运用中,先定义一个矩阵 Z ∈ R d × ∣ V ∣ Z∈R^{d\times |V|} Z∈Rd×∣V∣, d d d维表示embedding space的维度, ∣ V ∣ |V| ∣V∣表示节点的数量。即 Z Z Z中的每一列都代表这一个节点的embedding。

对于原始图中的节点表示,可以使用one-hot编码来表示;在我们训练模型学习到最佳的矩阵 Z Z Z后,编码器只是一个嵌入查找:
E N C ( v ) = z v = Z ⋅ v ENC(v)=z_v=Z\cdot v ENC(v)=zv=Z⋅v
这种方式的缺点:
Z
Z
Z的维度与节点数成正比,因此难以运用于大图中。
获取矩阵 Z Z Z的方式有很多种,经典的有:
- Deep Walk
- node2vec
三、Random Walk Approaches for Node Embeddings
符号规定:
-
z u z_u zu:
一个列向量,表示节点 u 的 u的 u的 e m b e d d i n g embedding embedding -
P ( v ∣ z u ) : P(v|z_u): P(v∣zu):
从 u u u节点开始随机游走,游走过程中遍历到 v v v节点的(预测的)概率。 -
σ ( z ) σ(z) σ(z)
Softmax函数, σ ( z ) [ i ] = e z [ i ] ∑ j = 1 K e z [ j ] σ(z)[i]=\frac{e^{z[i]}}{\sum_{j=1}^{K}e^{z[j]}} σ(z)[i]=∑j=1Kez[j]ez[i] -
S ( x ) S(x) S(x):
Sigmoid函数, S ( x ) = 1 1 + e − x S(x)=\frac{1}{1+e^{-x}} S(x)=1+e−x1
R a n d o m W a l k : Random\ Walk: Random Walk:
给定一个图和一个起点,随机选择它的一个邻居,并移动到这个邻居;然后我们随机选择这个点的一个邻居,并移动到它,迭代进行下去。以这种方式访问的点的(随机)序列成为在图上的随机游走。

随机游走路径上的节点在图中的距离是比较近的,所以相似度会较大,则路径上的顶点对的embedding内积也会相对较大,而embedding的内积是节点对在embedding space上的相似度。
因此可以得到下式:
z u T z v ≈ u 和 v 节点共同出现在一条随机游走路径上的概率 z_u^Tz_v≈u和v节点共同出现在一条随机游走路径上的概率 zuTzv≈u和v节点共同出现在一条随机游走路径上的概率
我们希望出现在一条随机游走路径上的节点对的embedding的内积值会较大。
Random-Walk Embeddings流程:
-
估计从节点 u u u为起点,以随机行走策略 R R R随机行走中访问节点 v v v的概率 P R ( v ∣ u ) P_R(v|u) PR(v∣u)

-
优化embeddings以最大化 P R ( v ∣ u ) P_R(v|u) PR(v∣u),优化embeddings的过程也相当于优化encoder了。

W h y R a n d o m W a l k s ? Why\ Random\ Walks? Why Random Walks?
-
Expressivity:
节点相似度的定义灵活随机,且结合了局部和高阶邻域的节点信息。- Idea:
如果从节点u开始的随机游走以高概率访问v,则u和v相似(高阶多跳信息)
- Idea:
-
Efficiency:
训练时不需要考虑所有节点对;只需要考虑在随机行走中同时出现的对
Random-Walk来寻找Node Embeddings,可以看作是一个半监督的feature learning。
-
目标:
找到在d维空间中保留相似性的节点嵌入。 -
要求:
学习Node Embeddings,使图中邻近的节点在d维空间中靠得很近
给定一个节点 u u u,如何定义 u u u在图中的邻近的节点呢?
以 u u u为起点,用随机游走策略 R R R进行游走,过程中访问到的节点可以当作 u u u的邻近节点 N R ( u ) N_R(u) NR(u)。
embedding feature的优化:
-
给定一个图 G ( V , E ) G(V,E) G(V,E)
-
我们的目标是学习一个映射函数 f : u → R d : f ( u ) = z u f:u→R^d:f(u)=z_u f:u→Rd:f(u)=zu
-
Log-likelihood objective:

- N R ( u ) N_R(u) NR(u):以游走策略 R R R游走 u u u的邻近节点
- 该式含义(个人理解):
邻近节点在原始图中距离较近,相似度会较大。在新的空间中,希望能够保持这个信息。 P ( N R ( u ) ∣ Z u ) P(N_R(u)|Z_u) P(NR(u)∣Zu)通过d维空间的向量 z u z_u zu来预测邻近节点出现在随机游走路径上的概率,希望这个概率越大越好。越大说明我能够通过 z u z_u zu来确定这几个邻近节点,这表明保留了原来的信息。
-
给定节点u,可以通过预测邻近节点的在随机游走路径中出现的概率来学习u的embedding feature。
R a n d o m W a l k O p t i m i z a t i o n : Random\ Walk\ Optimization: Random Walk Optimization:
-
使用随机漫步策略R,从图中的每个节点 u u u开始运行较短的固定路径长度的随机游走。
-
对每个顶点 u u u,收集其邻近顶点 N R ( u ) N_R(u) NR(u)
-
优化embeddings通过:给定一个节点 u u u,预测它的邻近节点 N R ( u ) N_R(u) NR(u)。即最大化下式:

-
定义损失函数:
上式添加负号,变成最小化,即希望该值越小越好。

最小化 L L L,即优化嵌入特征z,以最大化随机游走过程中, u u u和 v v v共同出现的可能性 -
将 P ( v ∣ z u ) P(v|z_u) P(v∣zu)使用softmax进行定义:

分母的作用:标准化。
最大化这个概率,可以理解为,在预测所有顶点对同时出现在同一条游走概率的时候,多分配些概率给 u u u和 v v v。 -
综上,我们要最小化的式子为:

优化 random walk embeddings=找到最小化 L L L的embeddings z u z_u zu -
采用随机梯度下降最小化函数 L L L。
有一个问题:
P
(
v
∣
z
u
)
P(v|z_u)
P(v∣zu)定义中,其分母需要遍历整张图的顶点对来计算,代价太大了。

希望能够采取某种策略计算出一个值,来近似接近这个值。
解决方案: N e g t i v e S a m p l i n g Negtive\ Sampling Negtive Sampling(负采样)
表征学习过程中,应尽量使每个中心节点与其邻居彼此靠近(嵌入向量相似)并远离所有其他节点。其他节点很多 ,为了减少计算成本,负采样 (NS)随机采样少量非邻居节点(负样本),中心节点只需要远离负样本即可。
即随机抽取 k k k个样本来进行标准化,替代使用所有顶点对进行标准化。如下图:

- 抽样k个负节点,节点的被抽取的概率与其度成比
- 如何选取
k
k
k?
- k越高,估计值越可靠
- k越高,负样本上的偏差bias越高
- 在实际中,k的选取为5-20
R a n d o m W a l k Random\ Walk Random Walk策略:
- 最简单的想法:从每个节点开始进行固定长度、无偏倚的随机行走。
- 代表:DeepWalk,存在的问题:相似度概念受限
-
n
o
d
e
2
v
e
c
node2vec
node2vec:
- 优点:有弹性的网络邻居 N R ( u ) N_R ( u ) NR(u)定义使 u u u的embedding更丰富,因此使用有偏的二阶随机游走策略 b i a s e d 2 n d o r d e r r a n d o m w a l k biased\ 2^{nd}\ order\ random\ walk biased 2nd order random walk以产生 N R ( u ) N_R(u) NR(u)
n o d e 2 v e c : B i a s e d W a l k s node2vec:Biased\ Walks node2vec:Biased Walks
思想:
使用灵活的、有偏差的随机游走,可以选择全局游走
D
F
S
DFS
DFS或者局部游走
B
F
S
BFS
BFS,生成信息更丰富的embeddings。

两种生成邻近节点的策略:
全局视角(DFS)和局部视角(BFS),BFS会汇聚局部邻域内节点的信息,而DFS会汇聚更远距离的顶点的信息。如下图:

B
F
S
v
s
.
D
F
S
BFS\ vs.\ DFS
BFS vs. DFS:

定义两个参数:
- return parameter
p
p
p:
回到前一个节点的概率的控制参数 - in-out parameter
q
q
q:
往外游走(DFS)和往内游走(BFS)的比值,即选择BFS和DFS的概率的控制参数。
node2vec是一个二阶随机游走策略:
node2vec会记住刚有走过的边
(
s
1
,
w
)
(s_1,w)
(s1,w)和现在所处的顶点
w
w
w。
即每一步游走都会关注两个信息:1.当前位置、2.从哪条路来的。根据这两个信息可以进行下一步决策:
- 回到之前的位置
- BFS
- DFS

对于下一步随机游走的路径选择,如下图所示:

为不同的边赋上不同的权重,得到一个未归一化的概率矩阵
P
r
o
b
Prob
Prob,通过将其归一化后根据概率选择其中一条边进行游走。
如果想要BFS-like walk,那么把p的值设小些;
如果想要DFS-like walk,那么把q的值设小些;
node2vec algorithm步骤:

上面三个步骤都是线性时间的复杂度,且可以独立并行的完成。