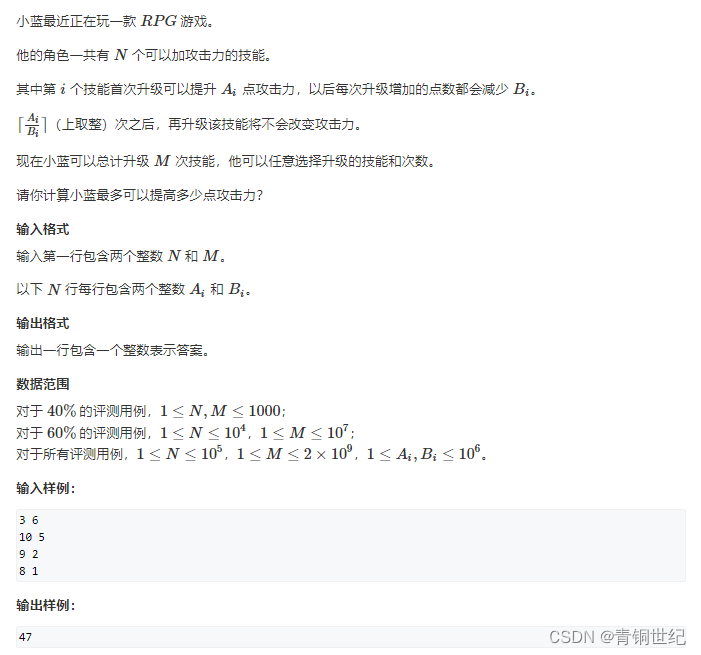
4656. 技能升级

https://www.acwing.com/problem/content/4659/

第十三届蓝桥杯省赛C++C组

算法标签：贪心；多路归并；二分

思路

• 如果暴力来做的话，会将所有数放到一个集合里面排序，取前 $m$ 项之和即可，但时间复杂度过高

• 如何优化？考虑我们只需要取前 $m$ 项，每一项范围在100万以内，可以使用二分来枚举一个分界点。由于分界点可能有多个（数值相等），我们只需要使大于x的数小于等于 $m$ 即可

  • 答案所在区间 $[0,1e6]$：由于 $m$ 可能超过有效升级次数，即答案中可能包含0

  • 由于每个序列都是等差数列，知道分界点后能够在 $O(1)$ 时间复杂度下求得该序列包含的个数以及总和。

    • 每个数列包含的个数: ceil((double) (a[i] - x) / b[i]) x为二分答案

    • 每个数列总和: int end = a[i] - b[i] * (t - 1); res += (ll)(a[i] + end) * t / 2;

      end 为末项

    • check(): 遍历每个大于x的数列首项，计算该数列包含的项数并累加，累加和小于等于 $m$ 时合法

  • 最后遍历每个数列首项，计算包含次数和总和，但这并不是最终答案，因为可能存在包含x的项。设 $cnt$ 为总次数，$m-cnt$ 则为包含x的项数，之前的求和再加上 $x\times (m-cnt)$ ($x$为二分答案)就是最终答案。

  • 看到这里可能会有疑问，为什么大小等于$x$的项数正好够用？即为什么 $m-cnt\le p$，设大小等于$x$的项数为$p$。因为在二分的时候已经确保 $cnt\le m$，$cnt+p>m$。如果 $cnt+p\le m$，则意味着 $x-1$ 也是合法的，与二分单调性相悖。

C++代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>

using namespace std;
typedef long long ll;
const int N = 1e5+10;
int n, m;

int a[N], b[N];

bool check(int x) {
    ll res = 0;
    for (int i = 0; i < n; i ++)
        if (a[i] > x) {
            res += ceil((double) (a[i] - x) / b[i]);
        }
    return res <= m;
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++) cin >> a[i] >> b[i];
    
    int l = 0, r = 1e6;
    
    while(l < r) {
        int mid = l + r >> 1;
        if (check(mid)) r = mid; // mid合法
        else l = mid + 1;
    }
    ll res = 0, cnt = 0;
    for (int i = 0; i < n; i ++)
        if (a[i] > l) {
            int t = ceil((double)(a[i] - l) / b[i]);
            cnt += t;
            int end = a[i] - b[i] * (t - 1); // 计算末项
            res += (ll)(a[i] + end) * t / 2; // 等差数列求和
        }
    printf("%lld\n", res + (ll)(m - cnt) * r); // 加上等于r的
    return 0;
}