文章目录
- 机器学习的概念和基础
- knn算法的实现过程
- 封装knn算法
- 总结
机器学习的概念和基础
机器学习可以两类任务: 分类任务和回归任务
以机器学习本身来进行分类可分为: 监督学习 非监督学习 半监督学习 增强学习
监督学习:给机器的训练数据 有标记label 有答案
- 猫狗识别
- mnist手写识别数据集 0 - 9 既有x,又有y(x为矩阵,代表样本特征,y代表样本目标值) 学习的算法大部分是监督学习的算法,但是不代表非监督学习不重要
非监督学习: 我们给机器的训练数据没有标记 没有答案
- 一般是用来辅助监督学习,比如对于没有标记的数据进行分类:聚类分析
- 对数据进行降维:
- 异常的样本
半监督学习:一部分有标记,一部分没有标记
增强学习:根据周围环境的情况,采取行动,然后根据行动的结果,学习行动的方式,非常适合机器人,例如alpha go zero
从其他维度对机器学习进行分类,可分为批量学习和在线学习
批量学习:模型固定,不会发生改变,面对新的数据,无法进行优化
- 问题:无法适应环境变化,比如垃圾邮件
- 解决方案:定时重新批量学习(成本巨大)
在线学习:不断的学习,应用模型 得到结果,同时不断的更新模型
- 优点: 及时反映新的环境变化
- 问题: 新的数据可能会带来不好的改变
- 解决方案: 加强数据的监控
knn算法的实现过程
本次以预测肿瘤为良性肿瘤或恶性肿瘤为例,先给出训练数据进行训练,获取模型,然后输入测试数据x,计算x与所有点的距离,并获取离x点最近的3个点,根据这三个点的类型(良性肿瘤或恶性肿瘤),哪种类型的肿瘤较多,则x很可能为该肿瘤类型。以上算法也可称之为k近邻算法(如下图)
观察下图,绿色为待预测点,离它最近的3个点有一个良性肿瘤(红色),两个恶性肿瘤(蓝色),因为恶性肿瘤数量>良性肿瘤,所以绿色的点很有可能为恶性肿瘤。

以下是程序编写过程
- 导入模块
import numpy as np
import matplotlib.pyplot as plt
- 准备训练数据,并将训练数据转换成矩阵
raw_data_X = [[3.3935, 2.3312],
[3.1101, 1.7815],
[1.3438, 3.3684],
[3.5823, 4.6792],
[2.2804, 2.8670],
[7.4234, 4.6965],
[5.7451, 3.5340],
[9.1722, 2.5111],
[7.7928, 3.4241],
[7.9398, 0.7916]]
raw_data_y =[0, 0, 0, 0, 0, 1, 1, 1, 1, 1] # 0是良性,1是恶性
# 训练数据,利用np.array将数据向量数据变为矩阵
X_train = np.array(raw_data_X)
y_train = np.array(raw_data_y)
- 给定待预测数据x,并绘制散点图。X_train[y_train==0,0]表示在X_train中取出y_train等于0的点,并取出这些点的第一个索引0,即横坐标。
# 给定待预测数据,预测他的结果
x = np.array([7, 3])
plt.scatter(X_train[y_train==0,0], X_train[y_train==0,1], color='r')
plt.scatter(X_train[y_train==1,0], X_train[y_train==1,1], color='b')
plt.scatter(x[0], x[1], color='g')
plt.show()

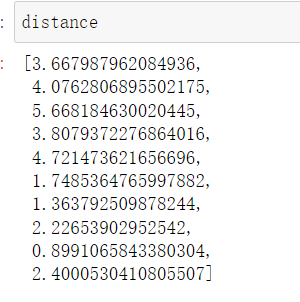
- 计算待预测点x与所有点的距离,并保存在distance列表中。计算所有点的距离使用到了欧拉距离公式,如下图,计算各向量的差值求平方,再相加,最后开根号。使用x_train-x,实现了各向量相减,减少了for循环的使用。
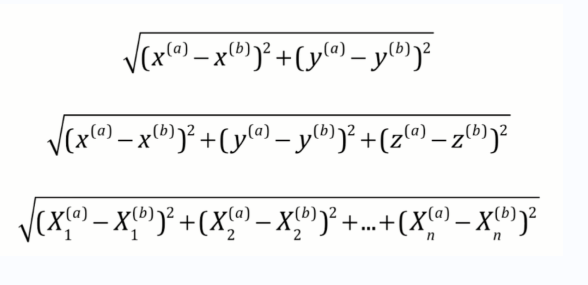
from math import sqrt
# 保存和其他所有点的距离
distance = [sqrt(np.sum((x_train-x)**2)) for x_train in X_train]
- 使用np.argsort(list),获取list中从小到大的值的索引,例如以下的np.argsort([1, 0, 5, 3]),结果得到的是[1, 0, 3, 2],其中1是list中0的索引,0为list中1的索引,3为list中3的索引,2为list中5的索引。

# 找出离待预测点距离最近的k个点
k = 3
nearest = np.argsort(distance)
nearest = [i for i in nearest[:k]]
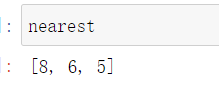
- 找出最近的k个点下标值,即[8, 6, 5],依据其在y_train中找出这些样本对应的目标值,观察下图即可知离待遇测点x最近的三个点为恶性肿瘤。
top_K = [i for i in y_train[nearest]]
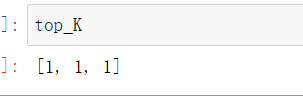
- 根据获取的top_K,使用collections中的Counter函数,获取最终投票结果,观察最终结果可以看到1有3票
from collections import Counter
votes = Counter(top_K)
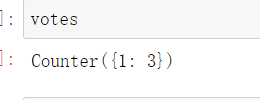
- 使用votes.most_common获取最终的投票结果,votes.most_common(1)[0][0]获取到最终投票结果,由图可知x点很可能为恶性肿瘤。

y_predict = votes.most_common(1)[0][0]
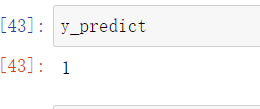
封装knn算法
将knn算法进行封装,并放在jupter notebook中运行,本次传入的待遇测数据为二维数据。
以下是封装浩的knn算法——knn.py
import numpy as np
from math import sqrt
from collections import Counter
# 在sklearn中,对于数据的拟合,创建模型,是放在fit方法中
class Knn:
def __init__(self, n_neighbor=3):
self.X_train = None
self.y_train = None
self.n_neighbor = n_neighbor
def fit(self, X_train, y_train):
# 给定X_train和y_train,得到训练模型
assert X_train.shape[0] == len(y_train) # 校验X_train的行数是否等于y_train的列数
self.X_train = X_train
self.y_train = y_train
# 返回对象的描述
return self
def predict(self, X):
# 对于给定的待预测数据,返回预测结果
assert self.X_train is not None
assert self.y_train is not None
assert self.X_train.shape[1] == X.shape[1] # 校验X_train的列数是否等于X的列数
return np.array([self._predict(x) for x in X])
def _predict(self, x):
# 给定一个样本求出一个结果
distance = [sqrt(np.sum((x_train - x)**2)) for x_train in self.X_train]
nearest = np.argsort(distance)
nearest = [i for i in nearest[:self.n_neighbor]]
top_K = [i for i in self.y_train[nearest]]
votes = Counter(top_K)
y_predict = votes.most_common(1)[0][0]
return y_predict
def __repr__(self):
# 返回对象的描述
return "KnnClassifier(n_neighbor=3)"
将封装好的knn算法放在项目同目录下,导入封装好的算法,进行计算。
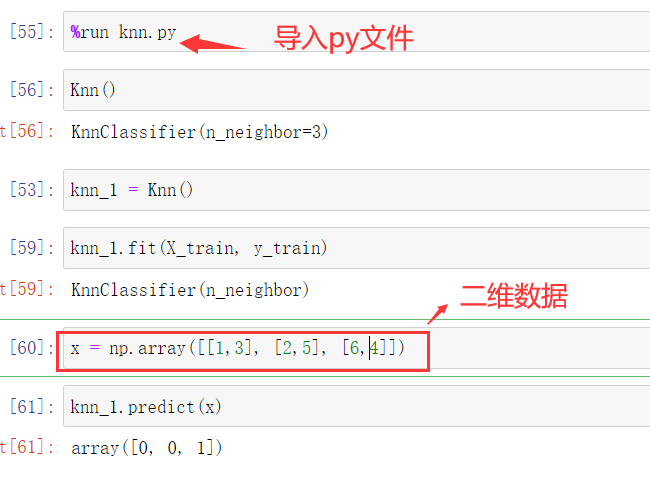
总结
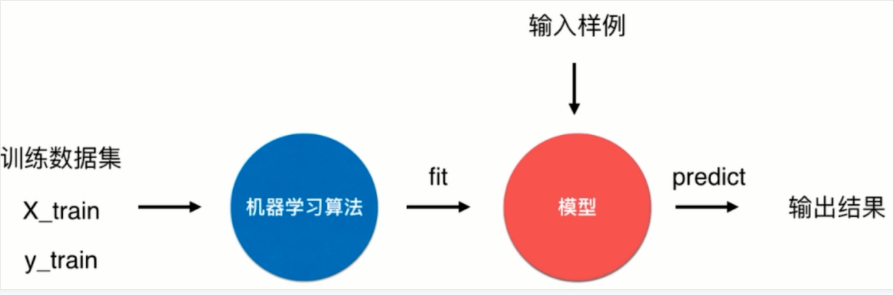
根据以上学习,我们可以总结出机器学习的算法实现过程如下图所示,先得到训练数据集,通过机器学习算法,使用fit方法对数据进行拟合,获取模型,最后通过输入样例(待预测数据),获得输出结果。