Softmax原理
Softmax函数用于将分类结果归一化,形成一个概率分布。作用类似于二分类中的Sigmoid函数。
对于一个k维向量z,我们想把这个结果转换为一个k个类别的概率分布p(z)。softmax可以用于实现上述结果,具体计算公式为:
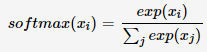
对于k维向量z来说,其中zi∈Rzi∈R,我们使用指数函数变换可以将元素的取值范围变换到(0,+∞)(0,+∞),之后我们再所有元素求和将结果缩放到[0,1],形成概率分布。
常见的其他归一化方法,如max-min、z-score方法并不能保证各个元素为正,且和为1。
Softmax性质
输入向量x加上一个常数c后求softmax结算结果不变,即:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5nEeYQfX-1673278208682)(null)]
我们使用softmax(x)的第i个元素的计算来进行证明:
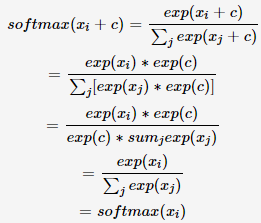
函数实现
由于指数函数的放大作用过于明显,如果直接使用softmax计算公式[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-c3Fqizxd-1673278208641)(null)]进行函数实现,容易导致数据溢出(上溢)。所以我们在函数实现时利用其性质:先对输入数据进行处理,之后再利用计算公式计算。具体使得实现步骤为:
- 查找每个向量x的最大值c;
- 每个向量减去其最大值c, 得到向量y = x-c;
- 利用公式进行计算 s o f t m a x ( x ) = s o f t m a x ( x − c ) = s o f t m a x ( y ) softmax(x) = softmax(x-c) = softmax(y) softmax(x)=softmax(x−c)=softmax(y)
import numpy as np
def softmax(x, axim=1):
'''
x: m*n m个样本,n个分类输出
return s:m*n
'''
row_max = np.max(x, axis=axis) # 计算最大值
row_max = row_max.reshape(-1, 1) # 将数据展开为m*1的形状,方便使用广播进行作差
x = x - row_max # 减去最大值
x_exp = np.exp(x) # 求exp
s = x_exp / np.sum(x_exp, axis=axis, keepdim=True) # 求softmax
return s
问题
过拟合和欠拟合的表现和解决方法。
其实除了欠拟合和过拟合,还有一种是适度拟合,适度拟合就是我们模型训练想要达到的状态,不过适度拟合这个词平时真的好少见,在做酷狗音乐的笔试题时还懵逼了一会,居然还真的有这样的说法。
这应该是基础中的基础了,笔试题都做烂了。那就当做今天周末,继续放个假吧……
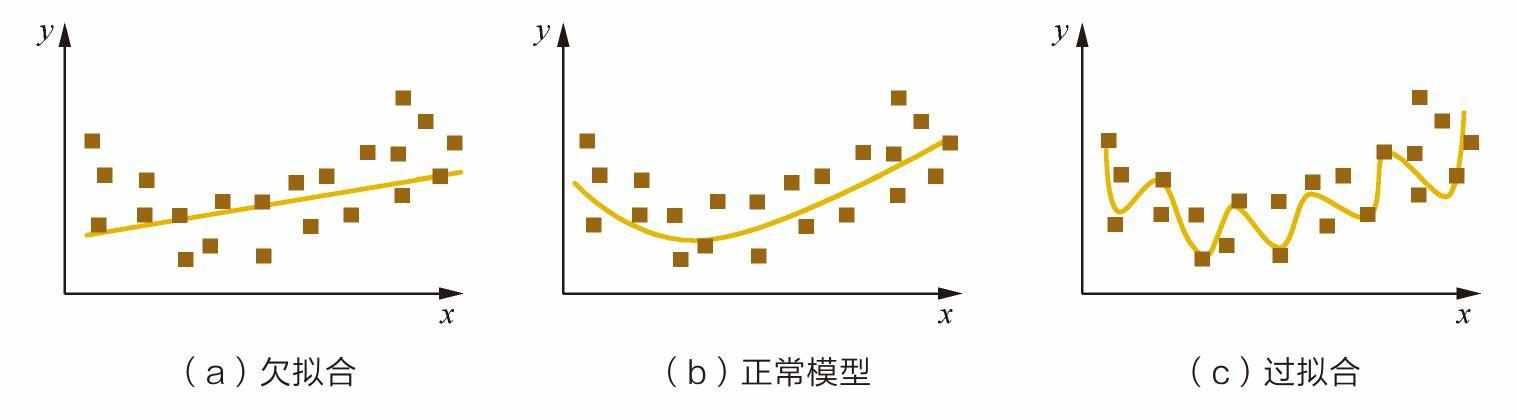
过拟合
过拟合的表现
模型在训练集上的表现非常好,但是在测试集、验证集以及新数据上的表现很差,损失曲线呈现一种高方差,低偏差状态。(高方差指的是训练集误差较低,而测试集误差比训练集大较多)
过拟合的原因
从两个角度去分析:
- 模型的复杂度:模型过于复杂,把噪声数据的特征也学习到模型中,导致模型泛化性能下降
- 数据集规模大小:数据集规模相对模型复杂度来说太小,使得模型过度挖掘数据集中的特征,把一些不具有代表性的特征也学习到了模型中。例如训练集中有一个叶子图片,该叶子的边缘是锯齿状,模型学习了该图片后认为叶子都应该有锯齿状边缘,因此当新数据中的叶子边缘不是锯齿状时,都判断为不是叶子。
过拟合的解决方法
-
获得更多的训练数据:使用更多的训练数据是解决过拟合问题最有效的手段,因为更多的样本能够让模型学习到更多更有效的特征,减少噪声的影响。
当然直接增加实验数据在很多场景下都是没那么容易的,因此可以通过数据扩充技术,例如对图像进行平移、旋转和缩放等等。
除了根据原有数据进行扩充外,还有一种思路是使用非常火热的**生成式对抗网络 GAN **来合成大量的新训练数据。
还有一种方法是使用迁移学习技术,使用已经在更大规模的源域数据集上训练好的模型参数来初始化我们的模型,模型往往可以更快地收敛。但是也有一个问题是,源域数据集中的场景跟我们目标域数据集的场景差异过大时,可能效果会不太好,需要多做实验来判断。
-
降低模型复杂度:在深度学习中我们可以减少网络的层数,改用参数量更少的模型;在机器学习的决策树模型中可以降低树的高度、进行剪枝等。
-
正则化方法如 L2 将权值大小加入到损失函数中,根据奥卡姆剃刀原理,拟合效果差不多情况下,模型复杂度越低越好。至于为什么正则化可以减轻过拟合这个问题可以看看这个博客,挺好懂的.。
添加BN层(这个我们专门在BN专题中讨论过了,BN层可以一定程度上提高模型泛化性能)
使用dropout技术(dropout在训练时会随机隐藏一些神经元,导致训练过程中不会每次都更新(预测时不会发生dropout),最终的结果是每个神经元的权重w都不会更新的太大,起到了类似L2正则化的作用来降低过拟合风险。)
-
Early Stopping:Early stopping便是一种迭代次数截断的方法来防止过拟合的方法,即在模型对训练数据集迭代收敛之前停止迭代来防止过拟合。
Early stopping方法的具体做法是:在每一个Epoch结束时(一个Epoch集为对所有的训练数据的一轮遍历)计算validation data的accuracy,当accuracy不再提高时,就停止训练。这种做法很符合直观感受,因为accurary都不再提高了,在继续训练也是无益的,只会提高训练的时间。那么该做法的一个重点便是怎样才认为validation accurary不再提高了呢?并不是说validation accuracy一降下来便认为不再提高了,因为可能经过这个Epoch后,accuracy降低了,但是随后的Epoch又让accuracy又上去了,所以不能根据一两次的连续降低就判断不再提高。一般的做法是,在训练的过程中,记录到目前为止最好的validation accuracy,当连续10次Epoch(或者更多次)没达到最佳accuracy时,则可以认为accuracy不再提高了。
-
集成学习方法:集成学习是把多个模型集成在一起,来降低单一模型的过拟合风险,例如Bagging方法。
如DNN可以用Bagging的思路来正则化。首先我们要对原始的m个训练样本进行有放回随机采样,构建N组m个样本的数据集,然后分别用这N组数据集去训练我们的DNN。即采用我们的前向传播算法和反向传播算法得到N个DNN模型的W,b参数组合,最后对N个DNN模型的输出用加权平均法或者投票法决定最终输出。不过用集成学习Bagging的方法有一个问题,就是我们的DNN模型本来就比较复杂,参数很多。现在又变成了N个DNN模型,这样参数又增加了N倍,从而导致训练这样的网络要花更加多的时间和空间。因此一般N的个数不能太多,比如5-10个就可以了。
-
交叉检验,如S折交叉验证,通过交叉检验得到较优的模型参数,其实这个跟上面的Bagging方法比较类似,只不过S折交叉验证是随机将已给数据切分成S个互不相交的大小相同的自己,然后利用S-1个子集的数据训练模型,利用余下的子集测试模型;将这一过程对可能的S种选择重复进行;最后选出S次评测中平均测试误差最小的模型。
欠拟合
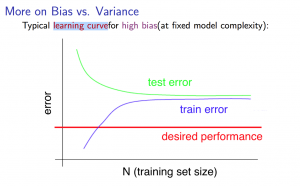
欠拟合的表现
模型无论是在训练集还是在测试集上的表现都很差,损失曲线呈现一种高偏差,低方差状态。(高偏差指的是训练集和验证集的误差都较高,但相差很少)
欠拟合的原因
同样可以从两个角度去分析:
- 模型过于简单:简单模型的学习能力比较差
- 提取的特征不好:当特征不足或者现有特征与样本标签的相关性不强时,模型容易出现欠拟合
欠拟合的解决方法
- 增加模型复杂度:如线性模型增加高次项改为非线性模型、在神经网络模型中增加网络层数或者神经元个数、深度学习中改为使用参数量更多更先进的模型等等。
- 增加新特征:可以考虑特征组合等特征工程工作(这主要是针对机器学习而言,特征工程还真不太了解……)
- 如果损失函数中加了正则项,可以考虑减小正则项的系数 λ \lambda λ
参考资料
过拟合与欠拟合及方差偏差 (这个博客总结地很好,可以看看)
《百面机器学习》
机器学习+过拟合和欠拟合+方差和偏差
如何判断欠拟合、适度拟合、过拟合