题目

给定一个整数 N，请你求出所有分母小于或等于 N，大小在 [0,1]范围内的最简分数，并按从小到大顺序依次输出。

例如，当 N=5时，所有满足条件的分数按顺序依次为：

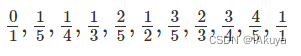
输入格式

共一行，包含一个整数 N。

输出格式

按照从小到大的顺序，输出所有满足条件的分数。

每个分数占一行，格式为 a/b，其中 a 为分子， b为分母。

数据范围

1≤N≤160

• 输入样例：

5

• 输出样例：

0/1
1/5
1/4
1/3
2/5
1/2
3/5
2/3
3/4
4/5
1/1

题解

最小公因数搜索

import java.util.*;

/**
 * @author akuya
 * @create 2024-03-17-21:43
 */
public class Main {
    static int N=160;
    static List<PII> list=new ArrayList<>();
    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        int n=scanner.nextInt();
        for(int i=1;i<=n;i++)
            for(int j=0;j<=i;j++)
                if(gcd(j,i)==1)
                    list.add(new PII(j,i));


        Collections.sort(list, new Comparator<PII>() {
            @Override
            public int compare(PII o1, PII o2) {
                return o1.a*o2.b-o1.b*o2.a;
            }
        });

        for(PII tp:list){
            System.out.println(tp.a+"/"+tp.b);
        }


    }


    public static int gcd(int a,int b){
        return b!=0 ? gcd(b,a%b):a;
    }
}

class PII{
    int a;
    int b;

    public PII(int a, int b) {
        this.a = a;
        this.b = b;
    }
}

Stern-Brocot Tree(不用理解，会用就行，一个数学原理)

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int n;

void dfs(int a, int b, int c, int d)
{
    if (a + c > n) return;

    dfs(a, b, a + c, b + d);
    printf("%d/%d\n", b + d, a + c);
    dfs(a + c, b + d, c, d);
}

int main()
{
    scanf("%d", &n);

    puts("0/1");
    dfs(1, 0, 1, 1);
    puts("1/1");

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/8041023/
来源：AcWing

思路

首先这是一道非常简单的题，因为数据量只有160，通过暴力也可以轻松通过，通过遍历再判断是否互质最后排序即可。

另一种思路是运用了Stern-Brocot Tree，一种数学思路模型，具体结果如下图，使用该方法就可以从小打大递归出所有的满足最简分数。具体方法流程如下图。

遍历函数具有两个参数a/b,c/d，那么a+c/b+d就是我们需要的函数，然后据需递归下去即可。