声明
本文章基于哔哩哔哩付费课程《小白也能听懂的人工智能原理》。仅供学习记录、分享,严禁他用!!如有侵权,请联系删除
目录
一、知识引入
(一)背景
(二)激活函数
(三)引入激活函数后
(四)梯度下降
1、复合函数求导--链式法则
2、引入激活函数后的代价函数e对w的导数
3、激活函数的意义
二、编程实验
(一)将sigmoid激活函数带入预测模型中
(二)复合函数的链式求导法则求出代价函数在w和b上的导数
(三)梯度下降
(四)完整代码
一、知识引入
(一)背景
人类在思考时,往往不会产生精确的数值估计或拟合,而更常做的事情是分类。eg:给定一个馒头,更倾向于将馒头分为“能吃饱”和“吃不饱”这两类,而不会在大脑中构建出一个精确的函数曲线。
对于小蓝也是,更希望把豆豆分成“有毒”和“无毒”这两类。
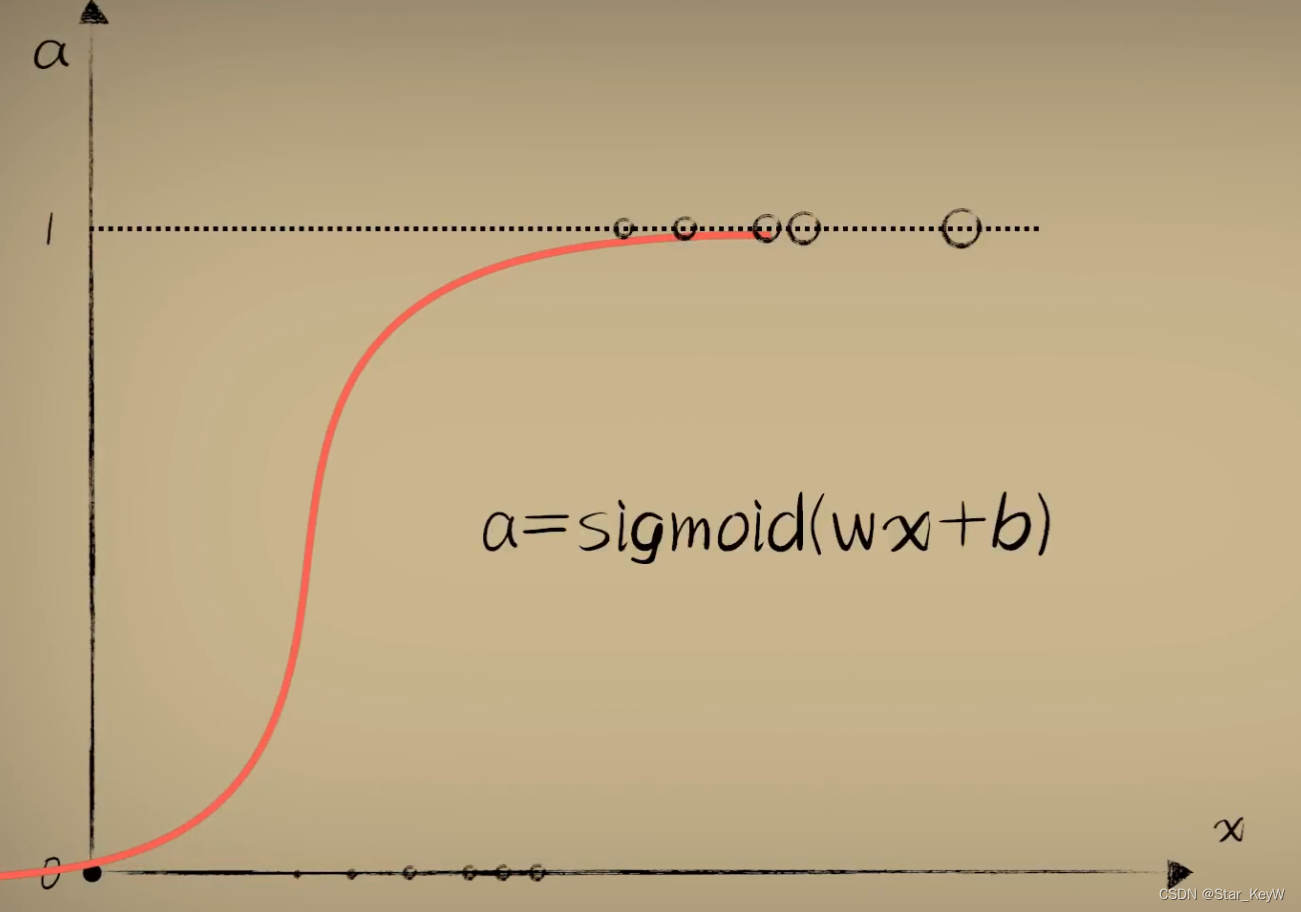
纵坐标不再表示毒性的大小,而表示有毒的概率,1表示有毒,0表示无毒。不存在中间值。是一个两级分类的分化问题。之前的预测函数y = wx + b变得不再适合。我们更希望可以在大于某个阈值时输出1,小于阈值时固定输出0。
(二)激活函数
可以利用一个分段函数实现这一点,把之前线性函数的结果,丢进一个分段函数中进行二次加工。这个新加入的分段函数就是--激活函数。
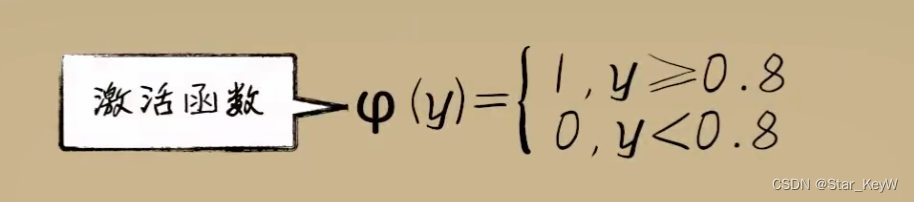
当然,这样的阶跃函数作为激活函数,并不十分美好。(导数处处为0,不利于梯度下降)
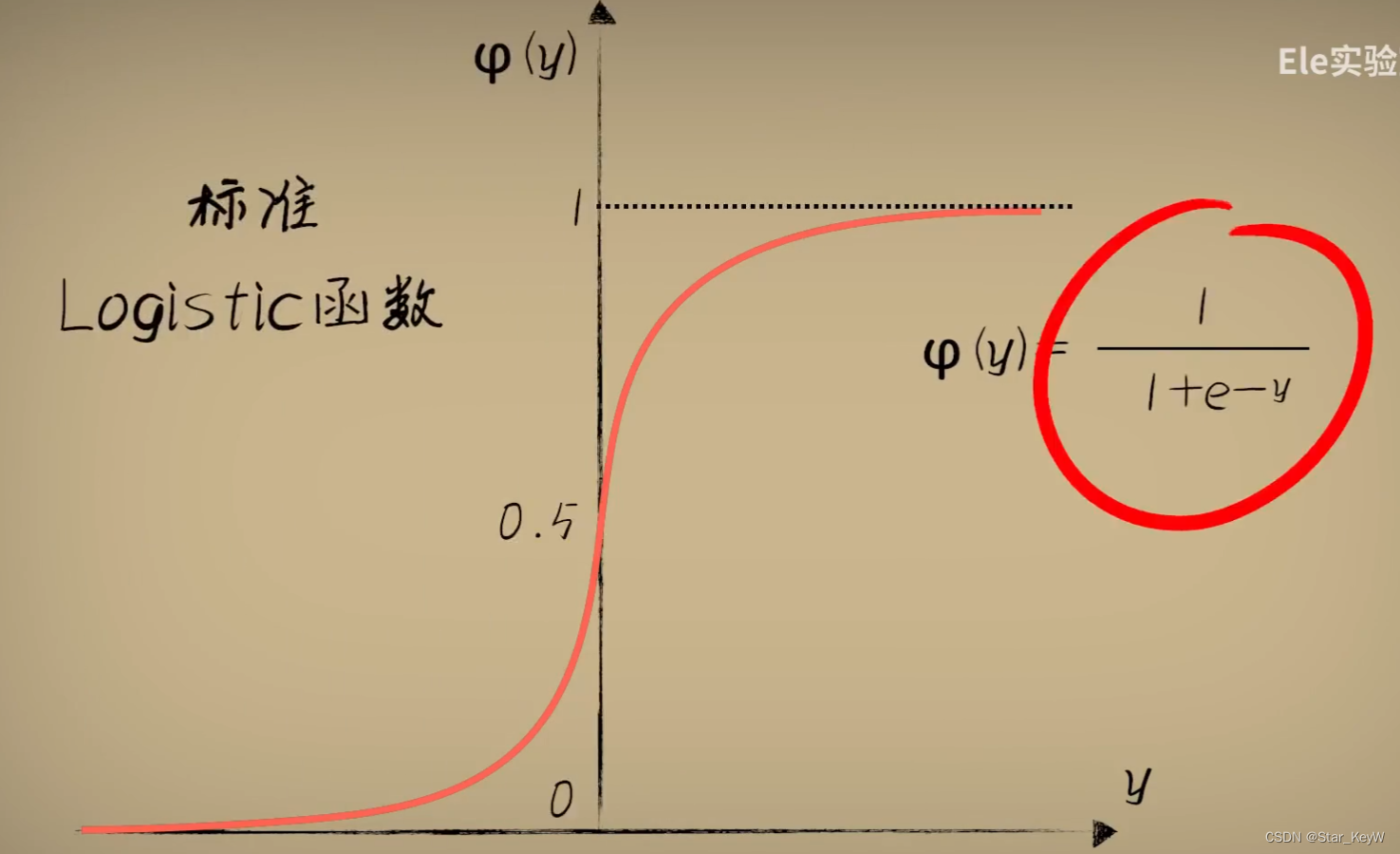
更好、更常用的函数--Logistic函数。标准的Logistic函数【圆润并且取值在[0,1],导数处处不为0】
(Sigmoid函数指的是一切具有S形状的函数,Logistic函数属于其中的一种,也是最常用的一种。
而Logistic我们一般也是使用他的标准形式,也就是取L=1,k=1,x0=0,这属于Logistic函数的一种特例。
这就是它们的区别,不过鉴于很多时候大家默认都是用标准的Logistic函数,所以慢慢的人开始就不主动区分Logistic和Sigmoid叫法,甚至不区分标准Logistic函数和sigmoid函数。
我们在机器学习中说的Sigmoid函数,一般也就指的是标准的Logistic函数。)
(三)引入激活函数后
线性函数现在作为预测的第一部分,线性函数的输出并不是最终的预测结果。
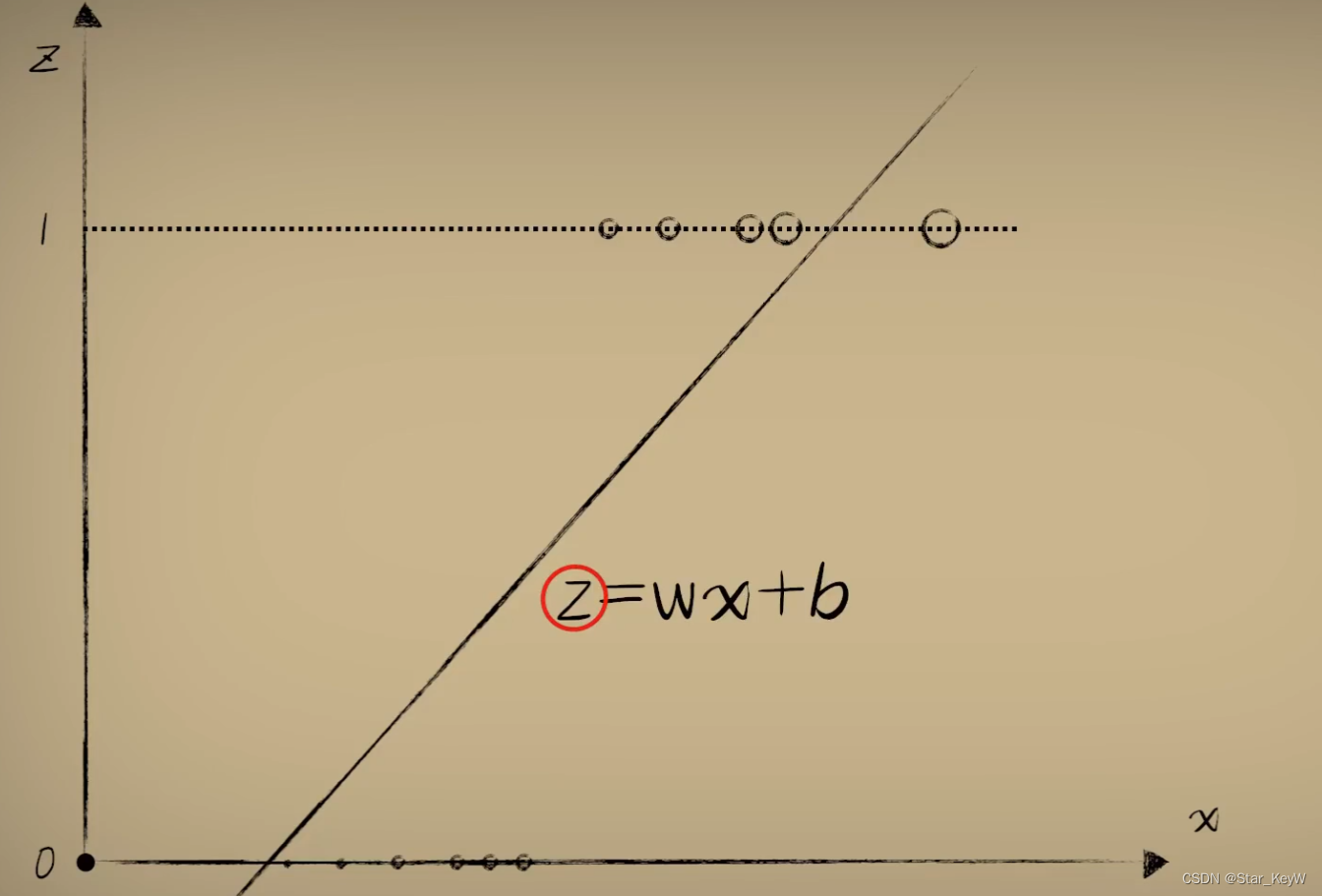
将线性函数的结果z,作为自变量,送入到激活函数中。
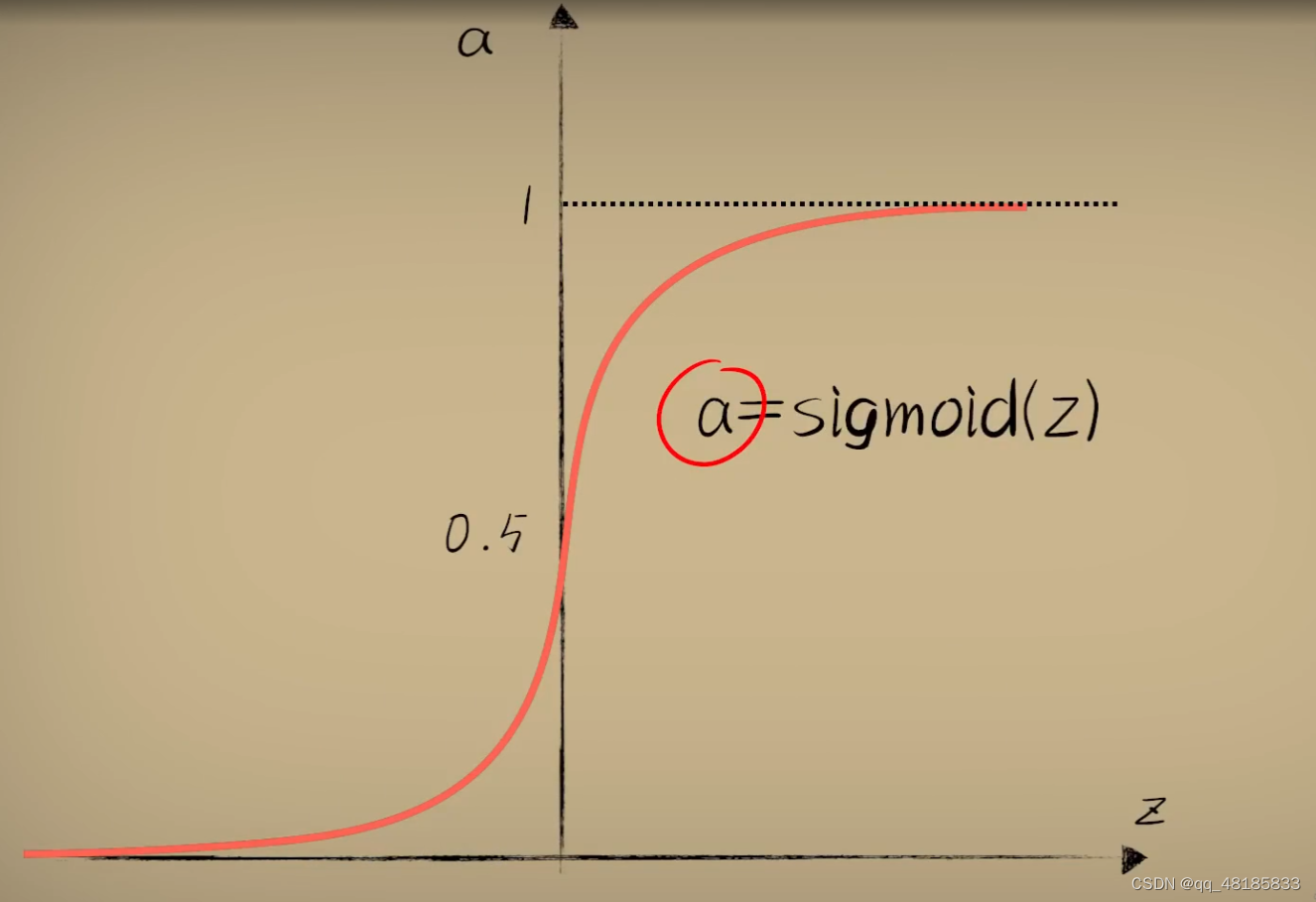
得到结果a,才是最后的预测结果。
(四)梯度下降
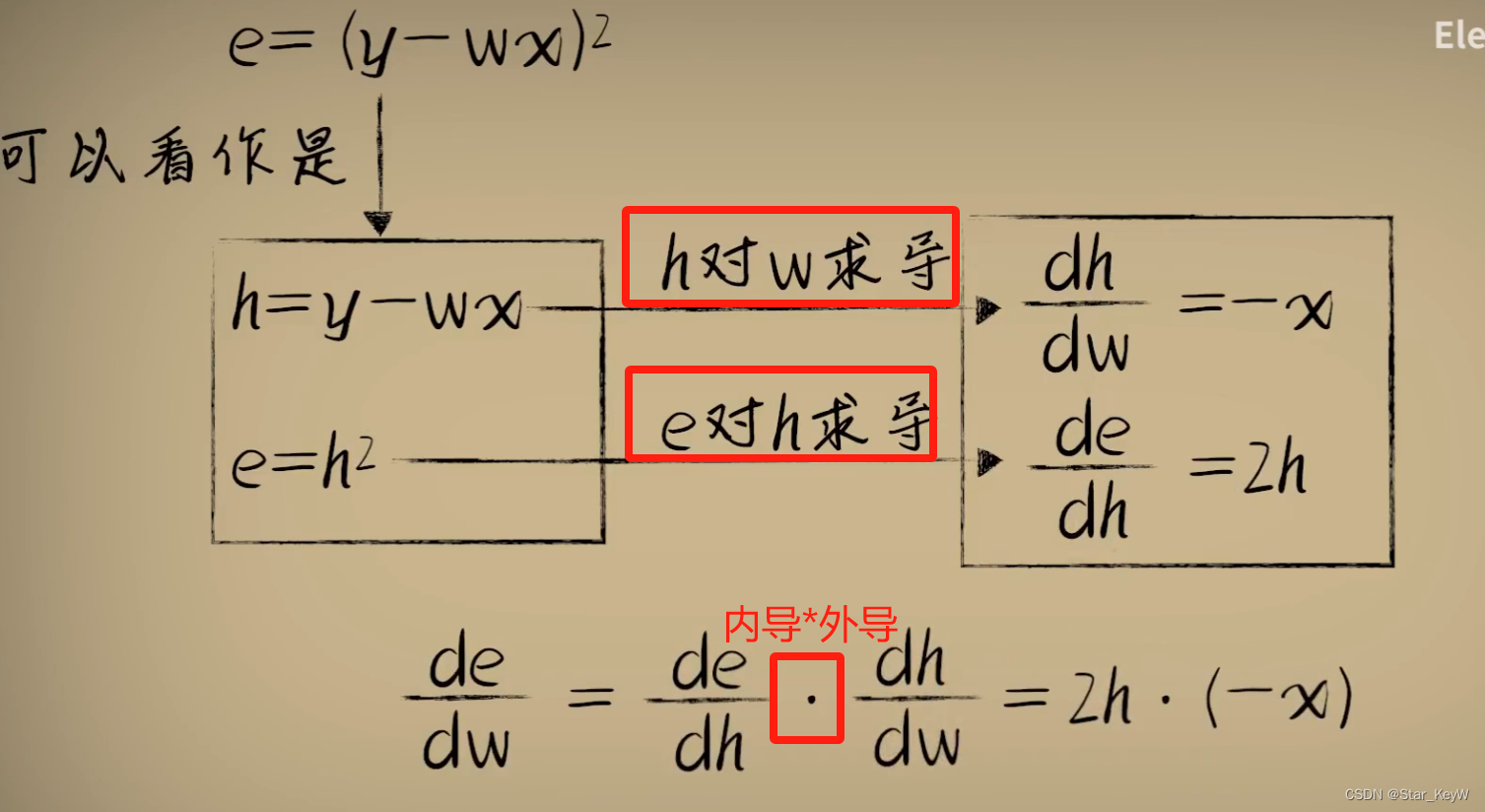
1、复合函数求导--链式法则
最终:
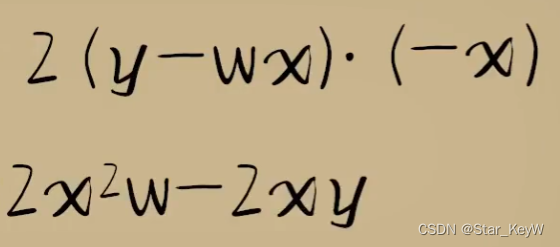
每一层分别把上一侧的因变量输出,作为本层的自变量输入进行求导。最后通过乘法相连。
2、引入激活函数后的代价函数e对w的导数
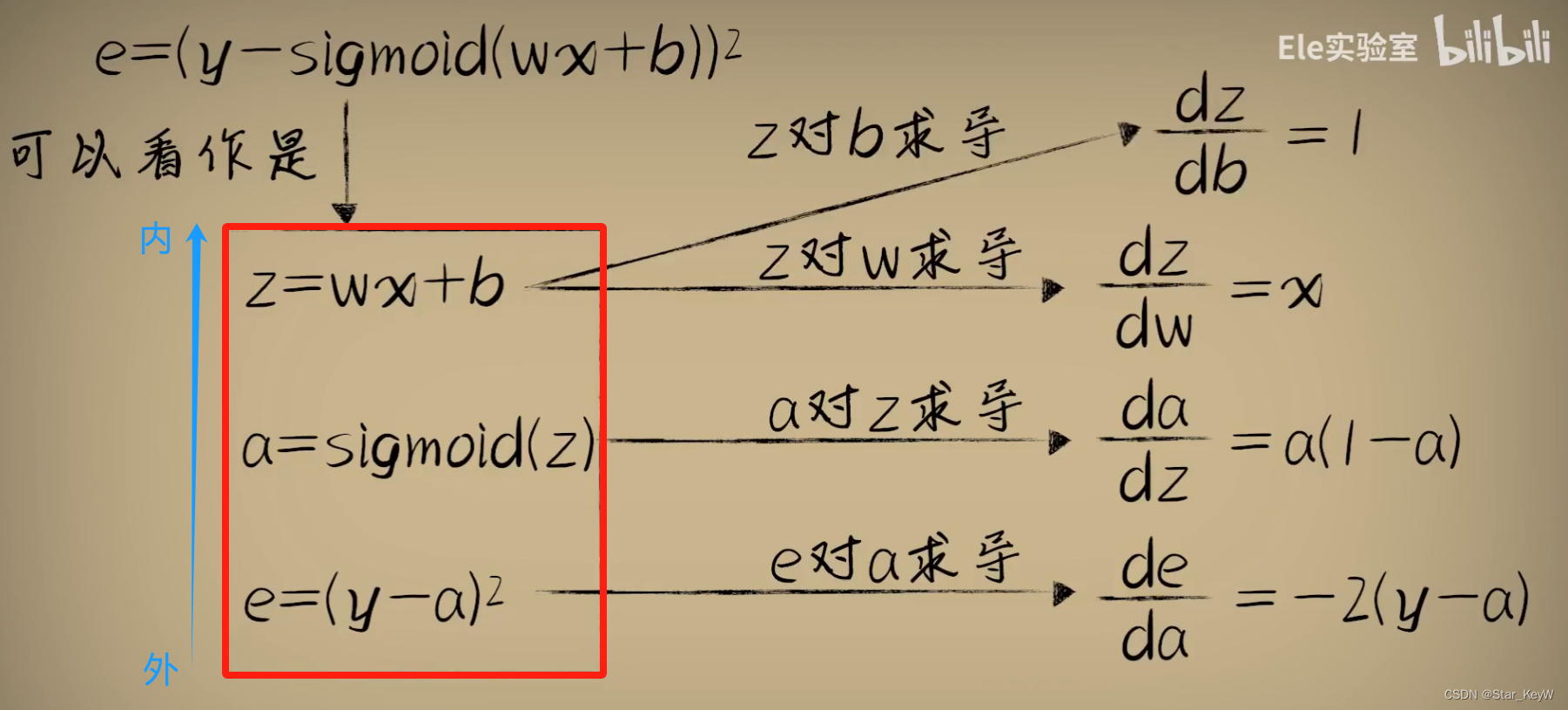
链式法则相乘:
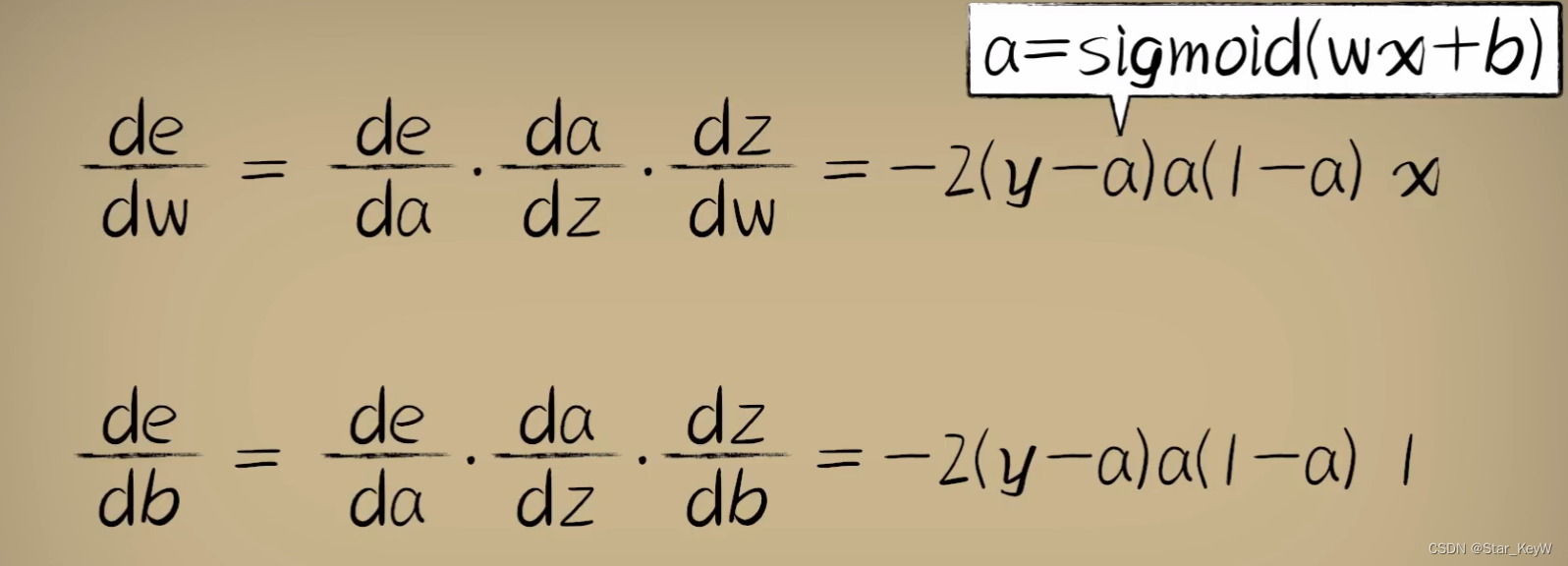
3、激活函数的意义
(1)线性函数能力有限,对于一个多层的神经网络,若每一个神经元都是一个线性函数,那么即使我们有很多的神经元构建出一个复杂神经网络,从数学的角度来说,他们在一起仍然是一个线性系统。线性函数无论怎么叠加,结果都是一个线性函数。
(2)激活函数是非线性的,让神经网络开始具备处理越来越复杂问题的能力。
二、编程实验
(一)将sigmoid激活函数带入预测模型中
w = 0.1
b = 0.1
z = w * xs + b
a = 1 / (1 + np.exp(-z))(二)复合函数的链式求导法则求出代价函数在w和b上的导数
# 对w和b求偏导
z = w * x + b
a = 1 / (1 + np.exp(-z))
# 损失函数
e = (y - a)**2
# 直接引入数学公式
deda = -2 * (y - a)
dadz = a * (1 - a)
dzdw = x
dedw = deda * dadz * dzdw
dzdb = 1
dedb = deda * dadz * dzdb(三)梯度下降
# 梯度下降
# 对b和w进行求导,二者合在一起,才算完成一次梯度下降
w = w - alpha * dedw # 梯度下降调整权重w
b = b - alpha * dedb # 梯度下降调整截距b(四)完整代码
import dataset
import matplotlib
import numpy as np
from matplotlib import pyplot as plt
# 首先要知道 matplotlib 的 backend 使用的是默认配置 agg (agg不能显示绘制的图),要想显示绘制的图需要更改 agg 为 TkAgg
matplotlib.use('TkAgg')
# 生成数据
xs, ys = dataset.get_beans(100)
num = 100
# 给定一个权重初始值
w = 0.1
b = 0.1
z = w * xs + b
# 使用sigmoid激活函数嘎变原始预测函数
a = 1 / (1 + np.exp(-z))
# 在全部样本上做了5000次梯度下降
for _ in range(5000):
for i in range(100):
x = xs[i]
y = ys[i]
# 对w和b求偏导
z = w * x + b
a = 1 / (1 + np.exp(-z))
# 损失函数
e = (y - a)**2
# 直接引入数学公式
deda = -2 * (y - a)
dadz = a * (1 - a)
dzdw = x
dedw = deda * dadz * dzdw
dzdb = 1
dedb = deda * dadz * dzdb
alpha = 0.05
# 梯度下降
# 对b和w进行求导,二者合在一起,才算完成一次梯度下降
w = w - alpha * dedw # 梯度下降调整权重w
b = b - alpha * dedb # 梯度下降调整截距b
# 减少绘图的频率
if _ % 50 == 0:
# plt.clf()函数清除绘图窗口
plt.clf()
# 重新绘制散点图和预测曲线
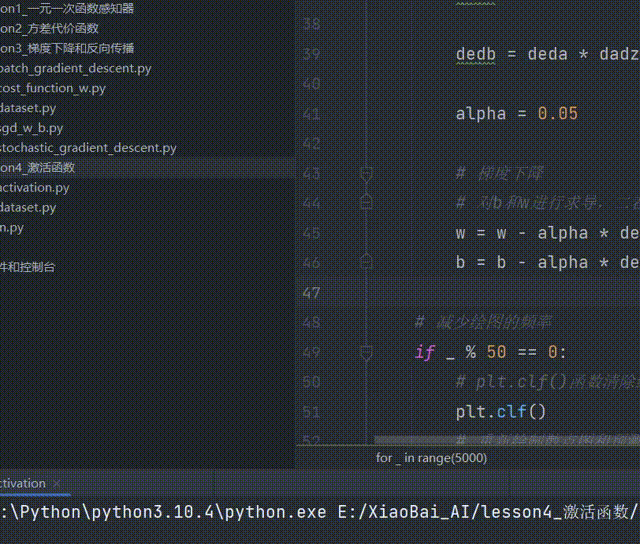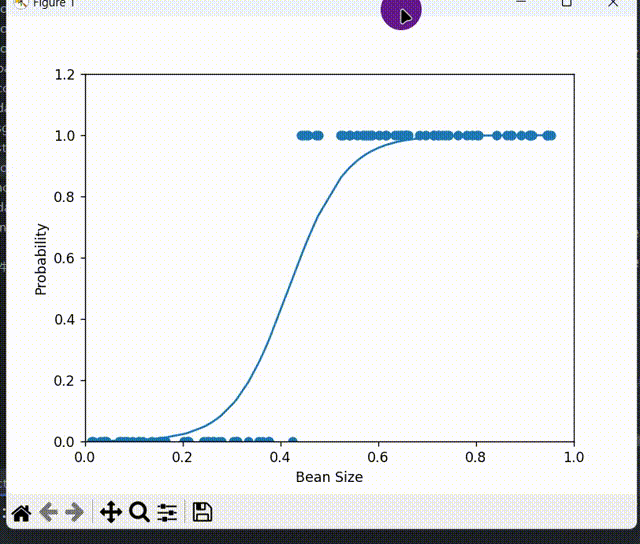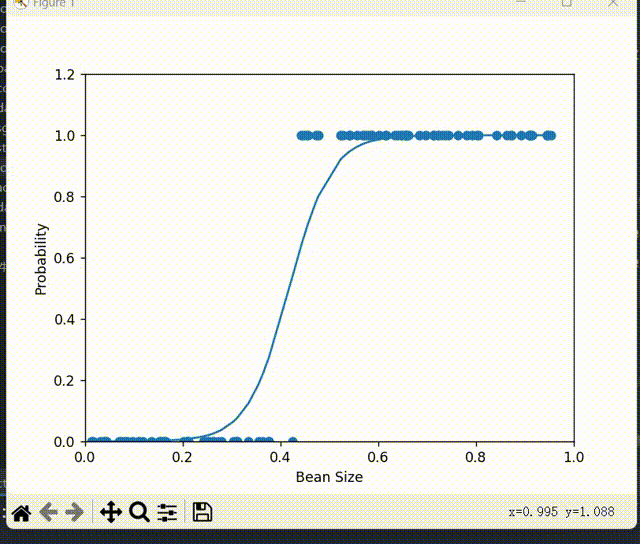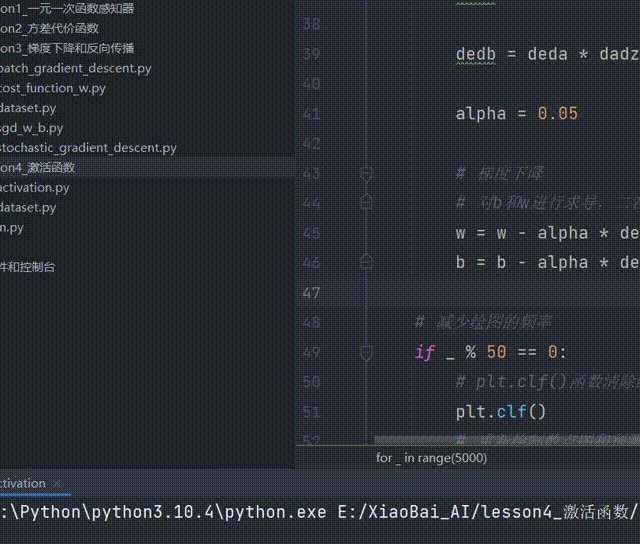
plt.scatter(xs, ys)
z = w * xs + b
a = 1 / (1 + np.exp(-z))
plt.xlabel("Bean Size") # 设置横坐标的名字
plt.ylabel("Probability") # 设置纵坐标的名字
# x轴的范围从0到1
plt.xlim(0, 1)
# y轴的范围从0到1.2
plt.ylim(0, 1.2)
plt.plot(xs, a)
# 暂停0.01秒
plt.pause(0.01)