本文将用可视化思路理解逻辑回归
数学背景
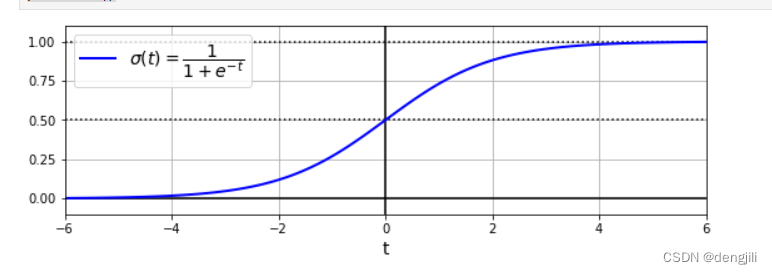
比如我们认定一个的值只可能在[0, 1], 那当小于0.5,我们认为他就是a,当大于0.5,我们认为他就是b
数据集
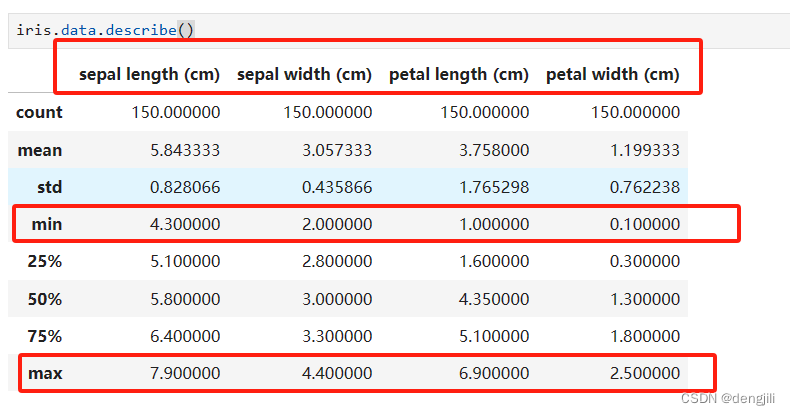
使用鸢尾花数据集
- 4个特征值
- 3个类别

二分类,单维度
- 只使用一个特征
X = iris.data[["petal width (cm)"]].values,方便可视化 - 使用
y = iris.target_names[iris.target] == 'virginica'方法,将3分类变成2分类,即判断是否为virginica
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
iris = load_iris(as_frame=True)
X = iris.data[["petal width (cm)"]].values
y = iris.target_names[iris.target] == 'virginica'
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
log_reg = LogisticRegression(random_state=42)
log_reg.fit(X_train, y_train)
可视化
X_new = np.linspace(0, 3, 1000).reshape(-1, 1) # reshape to get a column vector
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] >= 0.5][0, 0]
plt.figure(figsize=(8, 3)) # extra code – not needed, just formatting
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica proba")
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica proba")
plt.plot([decision_boundary, decision_boundary], [0, 1], "k:", linewidth=2,
label="Decision boundary")
plt.plot(X_train[y_train == 0], y_train[y_train == 0], "bs")
plt.plot(X_train[y_train == 1], y_train[y_train == 1], "g^")
plt.xlabel("Petal width (cm)")
plt.ylabel("Probability")
plt.legend(loc="center left")
plt.axis([0, 3, -0.02, 1.02])
plt.grid()
plt.show()
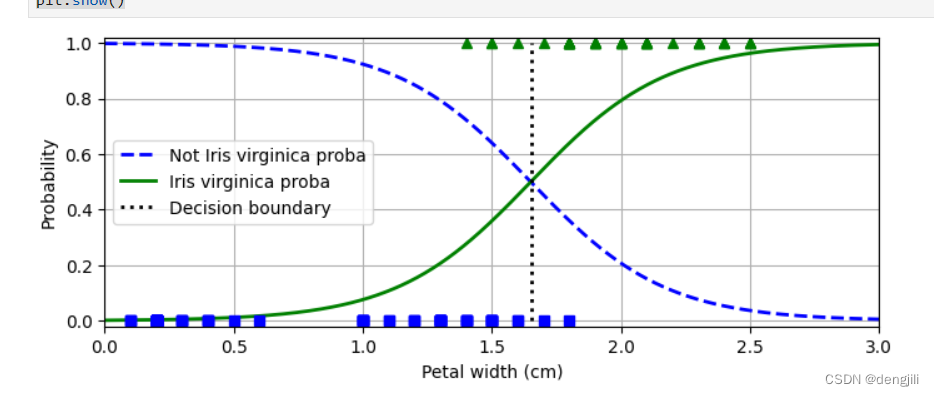
- 只分析单特征
Petal width (cm) - 分界线是
decision_boundary,当大于decision_boundary,是virginica花的可能性增大 - 分界线是
decision_boundary,当小于decision_boundary,是virginica花的可能性变小 - 主要看正方形和三角形,那是我们的训练样本,说明decision_boundary分界线只是一个推测,不是百分百,即概率推测
二分类,二维度
- “petal length (cm)”
- “petal width (cm)”
注意代码X = iris.data[["petal length (cm)", "petal width (cm)"]].values
X = iris.data[["petal length (cm)", "petal width (cm)"]].values
y = iris.target_names[iris.target] == 'virginica'
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
log_reg = LogisticRegression(C=2, random_state=42)
log_reg.fit(X_train, y_train)
可视化
x0, x1 = np.meshgrid(np.linspace(2.9, 7, 500).reshape(-1, 1),
np.linspace(0.8, 2.7, 200).reshape(-1, 1))
X_new = np.c_[x0.ravel(), x1.ravel()]
# X_new 长500*宽200=100000
# for the decision boundary
left_right = np.array([2.9, 7])
boundary = -((log_reg.coef_[0, 0] * left_right + log_reg.intercept_[0])
/ log_reg.coef_[0, 1])
plt.figure(figsize=(10, 4))
plt.plot(X_train[y_train == 0, 0], X_train[y_train == 0, 1], "bs")
plt.plot(X_train[y_train == 1, 0], X_train[y_train == 1, 1], "g^")
plt.plot(left_right, boundary, "k--", linewidth=3)
plt.text(3.5, 1.27, "Not Iris virginica", color="b", ha="center")
plt.text(6.5, 2.3, "Iris virginica", color="g", ha="center")
plt.xlabel("Petal length")
plt.ylabel("Petal width")
plt.axis([2.9, 7, 0.8, 2.7])
plt.grid()
plt.show()
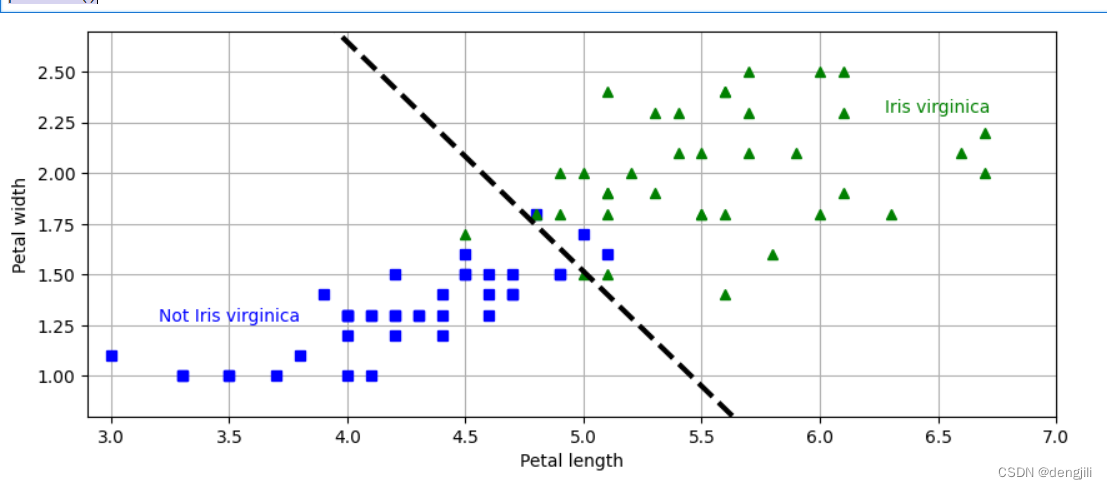
分析同单维度
多分类,二维度
- “petal length (cm)”
- “petal width (cm)”
注意代码y = iris["target"],已经不再只是判断是否为virginica
X = iris.data[["petal length (cm)", "petal width (cm)"]].values
y = iris["target"]
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
softmax_reg = LogisticRegression(C=30, random_state=42)
softmax_reg.fit(X_train, y_train)
可视化
# extra code – this cell generates and saves Figure 4–25
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(["#fafab0", "#9898ff", "#a0faa0"])
x0, x1 = np.meshgrid(np.linspace(0, 8, 500).reshape(-1, 1),
np.linspace(0, 3.5, 200).reshape(-1, 1))
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)
zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y == 2, 0], X[y == 2, 1], "g^", label="Iris virginica")
plt.plot(X[y == 1, 0], X[y == 1, 1], "bs", label="Iris versicolor")
plt.plot(X[y == 0, 0], X[y == 0, 1], "yo", label="Iris setosa")
plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap="hot")
plt.clabel(contour, inline=1)
plt.xlabel("Petal length")
plt.ylabel("Petal width")
plt.legend(loc="center left")
plt.axis([0.5, 7, 0, 3.5])
plt.grid()
plt.show()
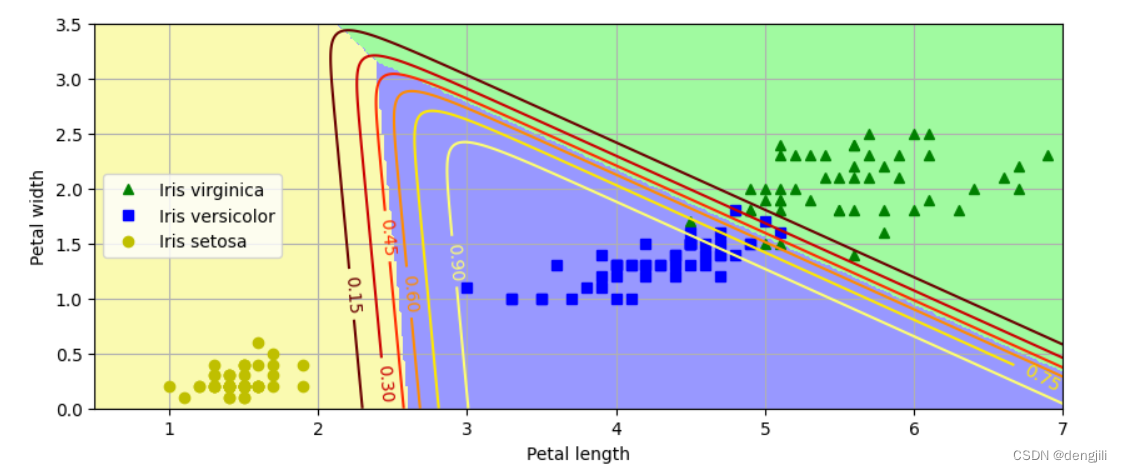
分析同上