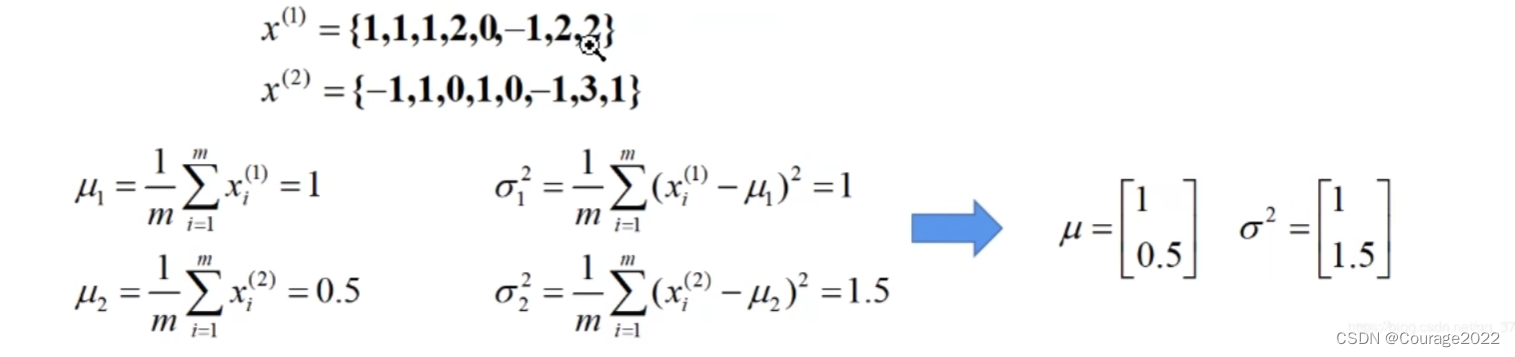1.ResNet简介

ResNet在2015年由微软实验室提出，斩获当年lmageNet竞赛中分类任务第一名，目标检测第一名。获得coco数据集中目标检测第一名，图像分割第一名。(啥也别说了，就是NB）。

网络中的亮点：

①超深的网络结构（突破1000层）

②提出residual模块
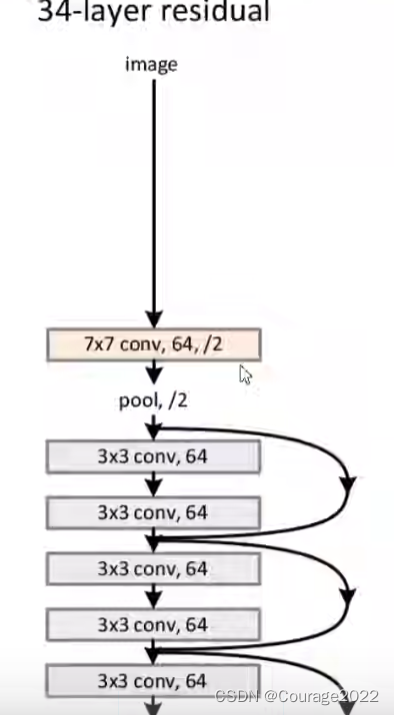
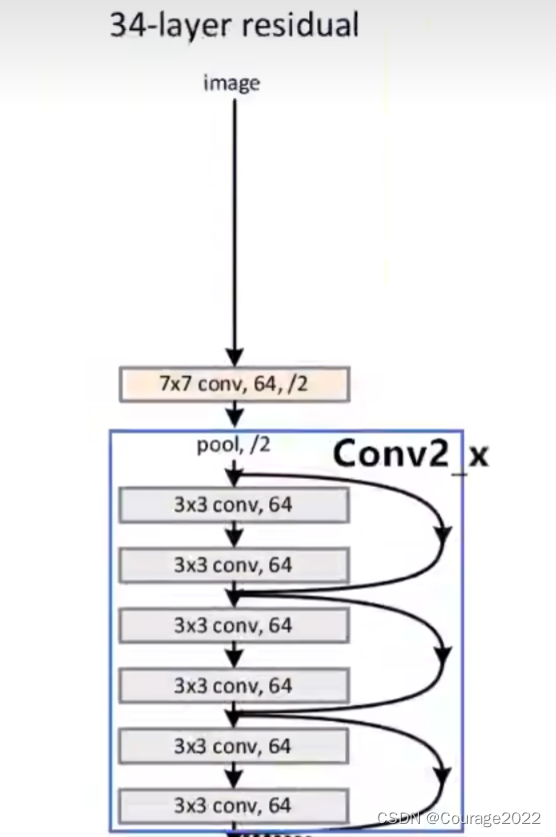
③使用Batch Normalization加速训练（丢弃dropout）

我们看看34层的残差网络的部分：

在我们的34层的ResNet网络中，首先是个卷积层、其次是个池化层，图中有连接线的结构就是一个残差结构，这个网络就是由一系列的残差结构组成的，最后拼接一个平均池化下采样操作和一个全连接层完成网络输出。

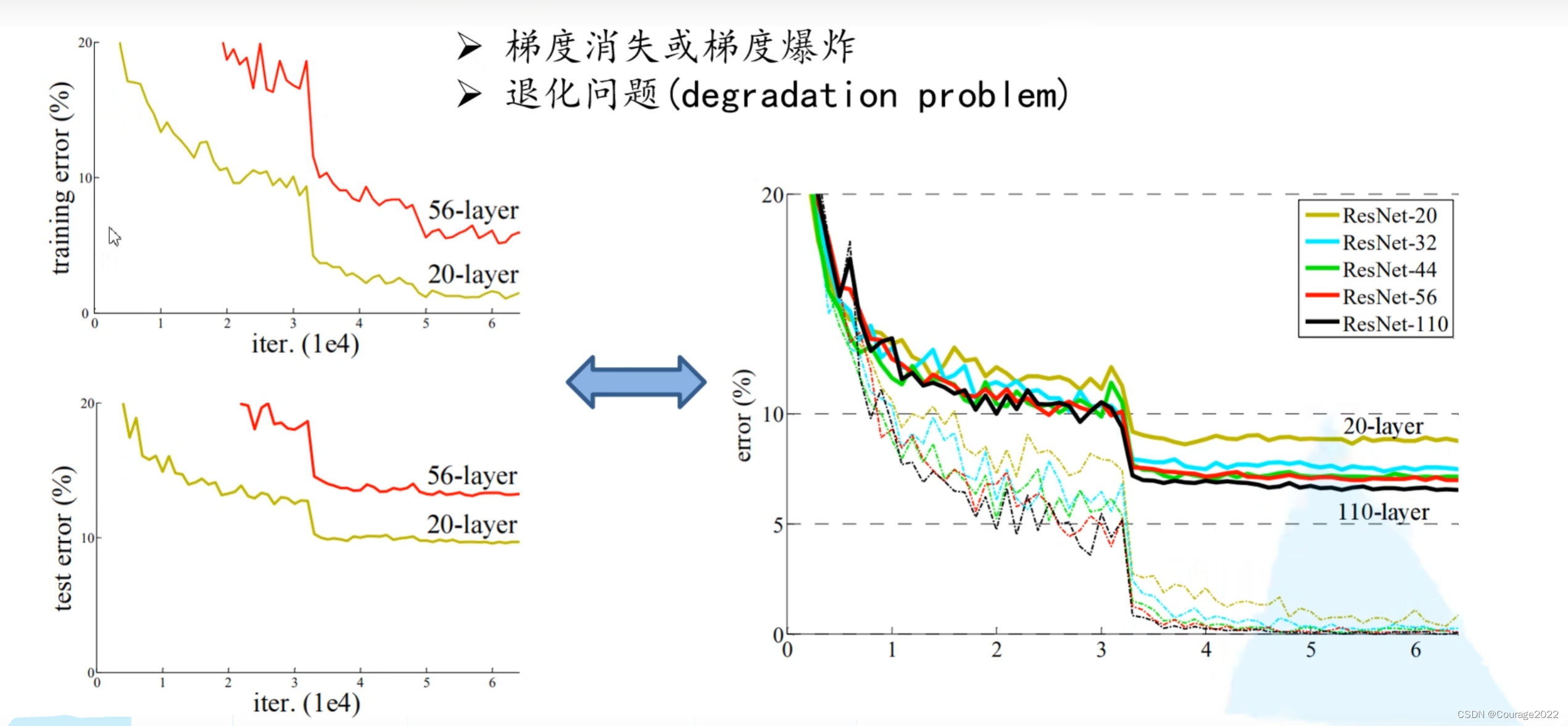
我们来看一下它的效果：

我们发现几个问题：并不是越深效果越好，因为有梯度消失梯度爆炸的问题。

如何解决这种问题：数据标准化处理、BN、权重归一化...

2.residual结构和ResNet-34详解

2.1 residual结构

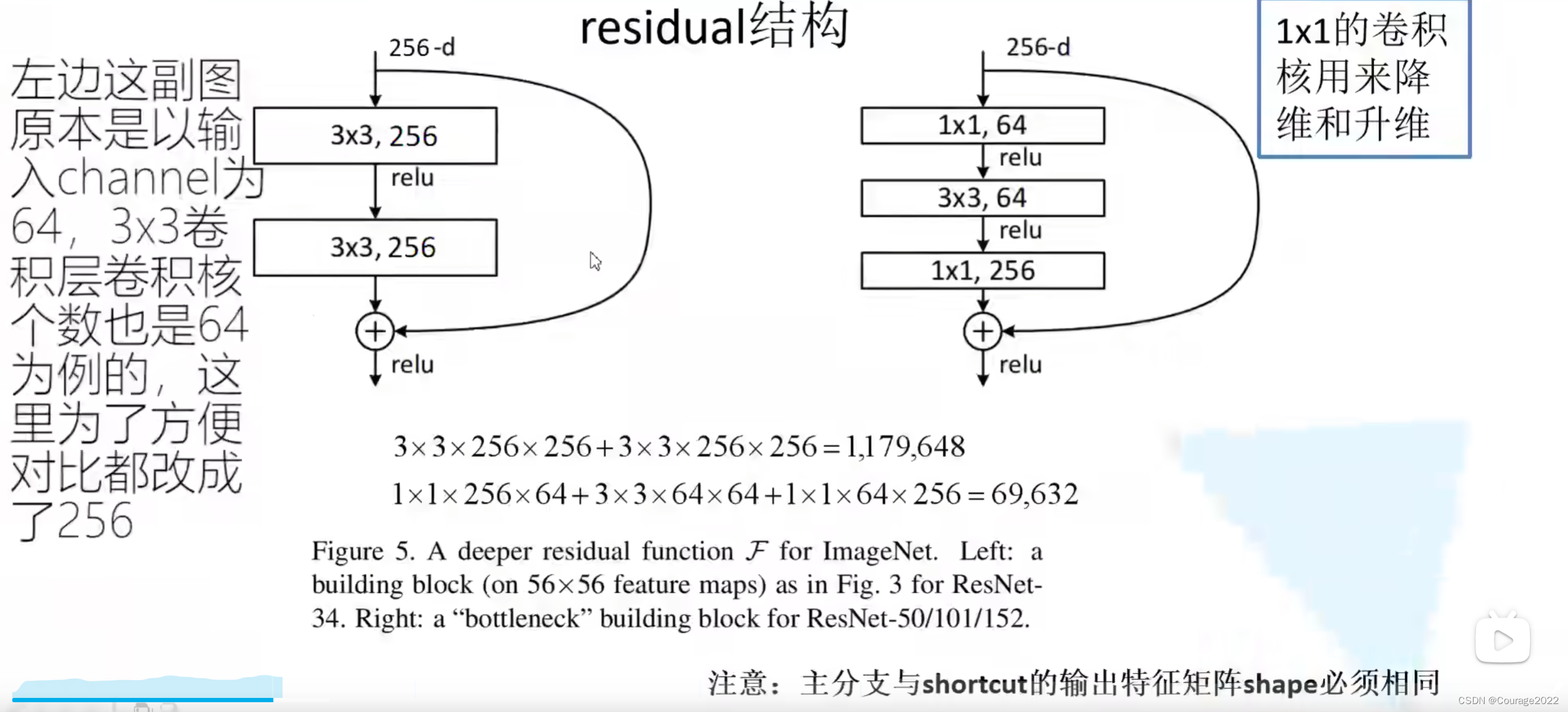
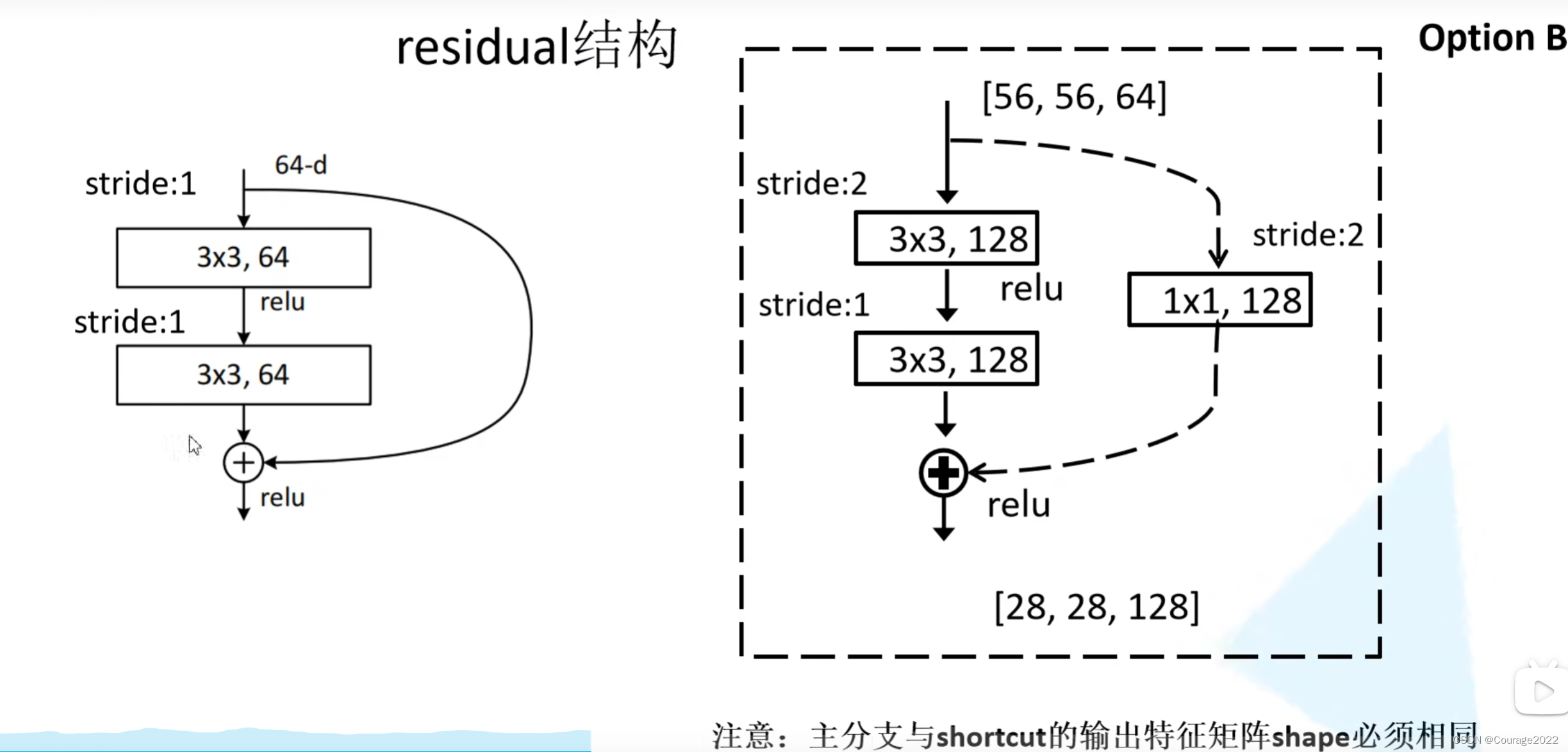
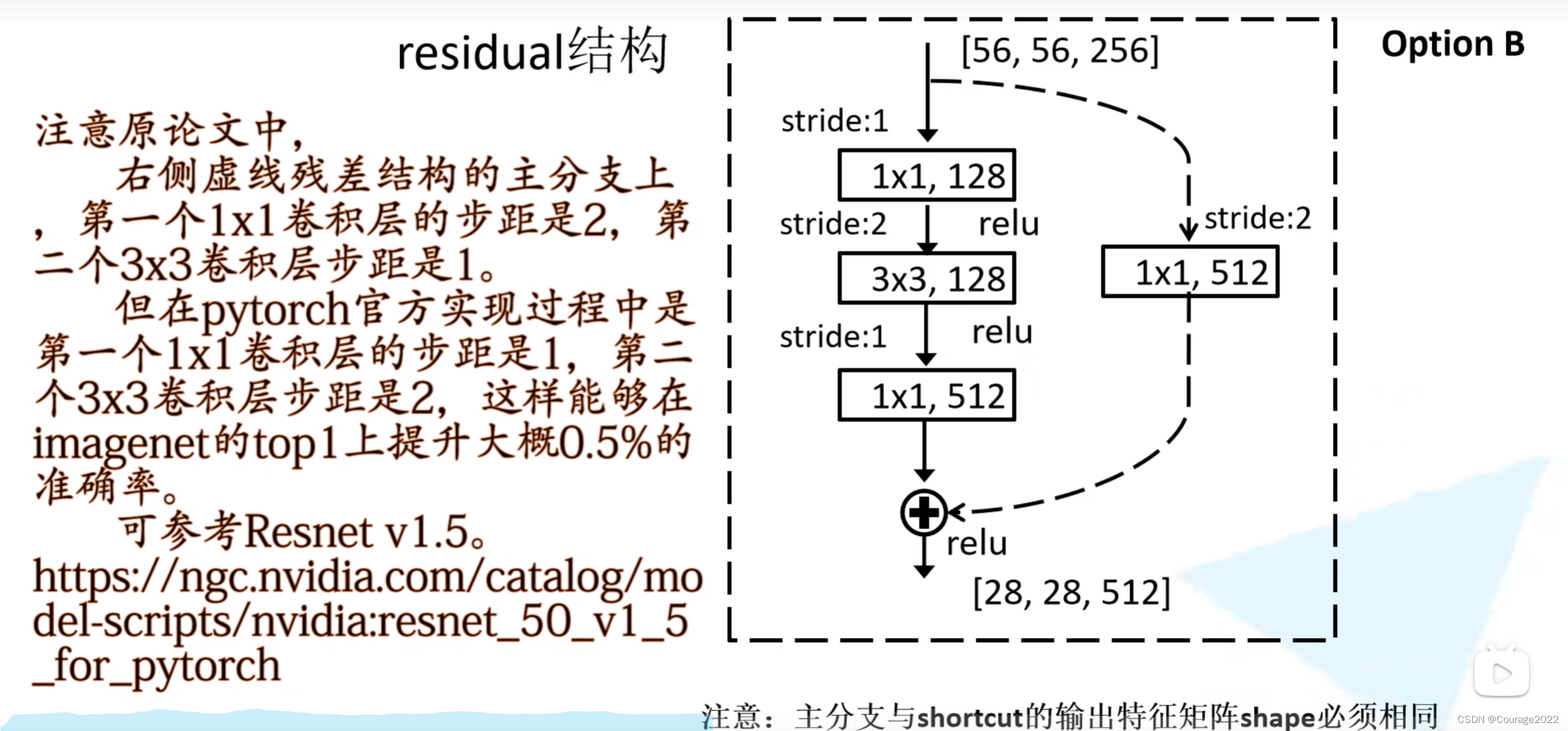
        我们来看两种不同的残差结构：左边主要针对网络层数较少的网络，右边主要针对网络层数较大的网络。

这里的残差指在主分支上经过一系列卷积层所得到的结果的特征矩阵再与我们输入特征矩阵进行相加，相加后再经过ReLU激活函数。

这里的 $1\times1$ 的卷积核主要用来改变通道数，那么这两个网络中参数有多少呢？

假设我们同样的输入一个256维的特征向量：

对于第一个特征矩阵：

3*3*256（卷积核参数）*256（卷积核个数，用256个卷积核保证输入输出channel相同），对于第二个卷积核，我们需要3*3*256*256个参数，加起来是1179648个参数。

        对于第二个特征矩阵：

1*1*256*64 + 3*3*64*64 + 1*1*64*256 = 69632个参数。

因此使用的残差结构越多，我们省下的计算资源也就越多。

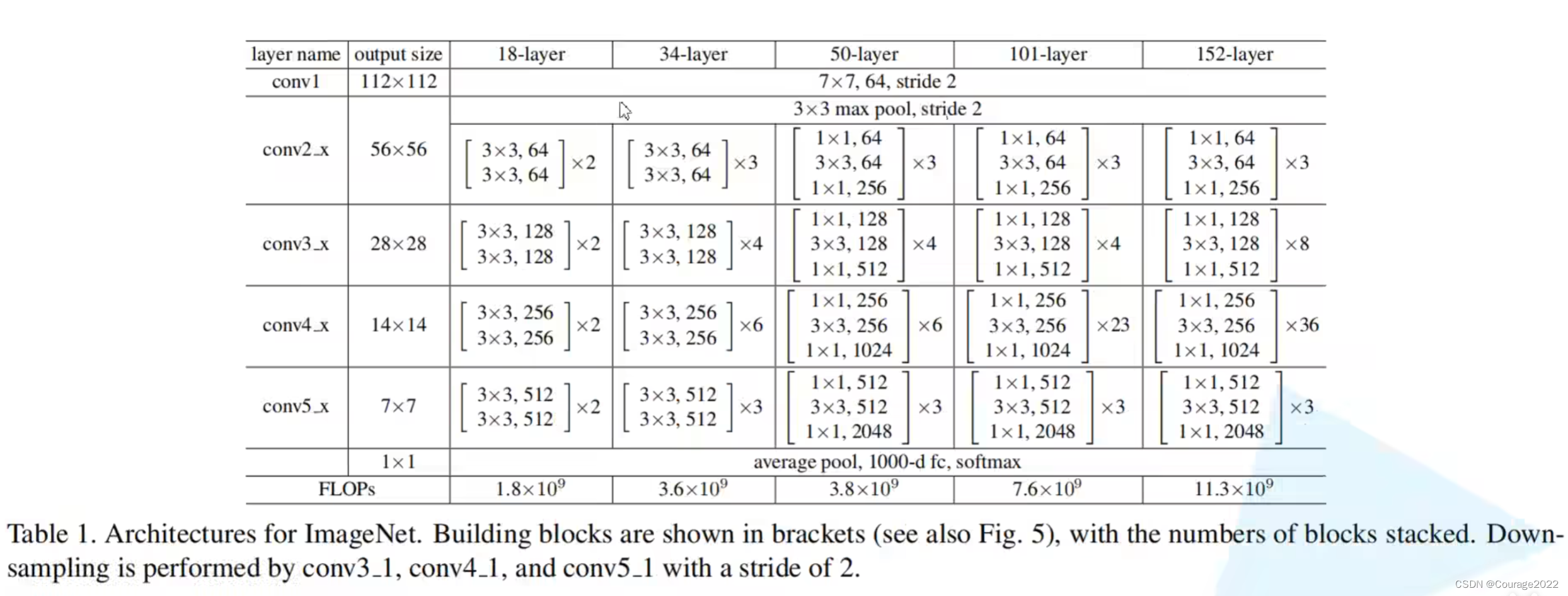
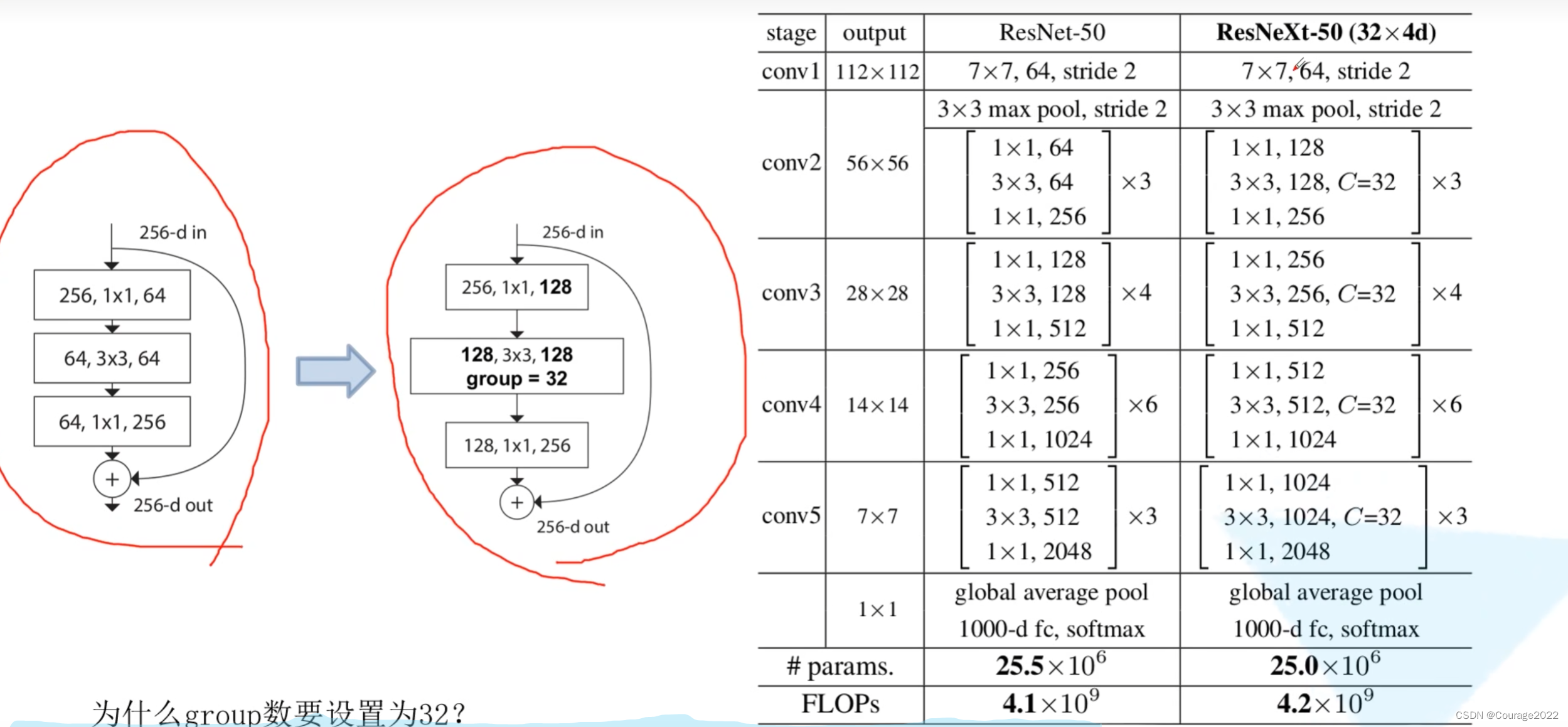
上表是论文中给出的网络结构。

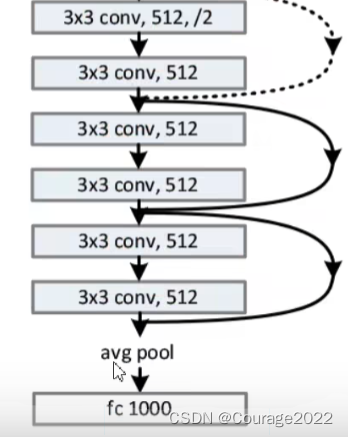
我们主要看一下34层的网络结构：

首先是个 $7\times7$ 的卷积核，下一层是一个 $3\times3$ 的最大池化下采样层。对于我们的Conv2_x的残差结构，这里使用了三层残差层。

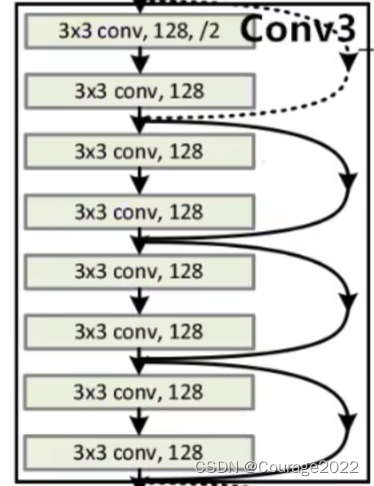
        对于我们的Conv3_x的残差结构，这里使用了四层残差层。

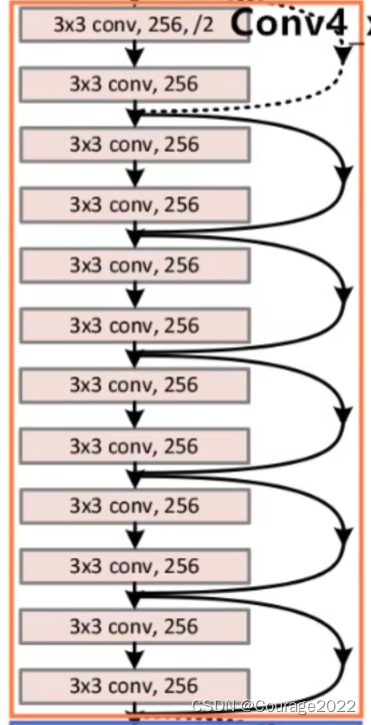
        对于我们的Conv4_x的残差结构，这里使用了六层残差层。

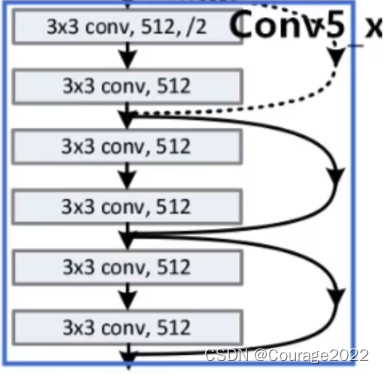
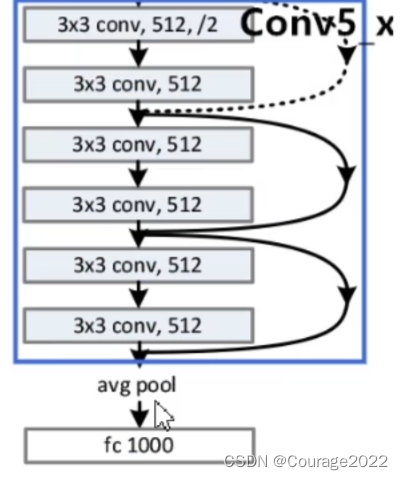
        对于我们的Conv5_x的残差结构，这里使用了三层残差层。

最后使用平均池化下采样和全连接层。

我们发现其有实线和虚线，它们是不一样的吗？

对于实线结构，它的输入特征矩阵的shape和输出特征矩阵的shape是完全一样的，直接进行相加；对于虚线的结构，它的输入特征矩阵的shape和输出特征矩阵的shape不是完全一样的。

这里对应我们的conv_3，它的输入特征矩阵的shape是 $56\times56\times64$ 的，它的输出特征矩阵的shape是 $28\times28\times 128$ 的，旁边的捷径保证了特征矩阵的高宽通道相同能够进行相加操作。

2.2 Batch Normalization

即特征矩阵每个channel对应的维度要满足均值为0，方差为1。

具体阐述请见博文：

BN详解https://blog.csdn.net/qq_37541097/article/details/104434557 “对于一个拥有d维的输入x，我们将对它的每一个维度进行标准化处理。” 假设我们输入的x是RGB三通道的彩色图像，那么这里的d就是输入图像的channels即d=3， $x=(x^{(1)},x^{(2)},x^{(3)})$ ，其中 $x^{(1)}$ 就代表我们的R通道所对应的特征矩阵，依此类推。标准化处理也就是分别对我们的R通道，G通道，B通道进行处理。上面的公式不用看，原文提供了更加详细的计算公式：

计算每一通道（一批数据同一通道的所有数据）的均值方差，将原参数减去均值除以方差得到标准化处理的数据，再根据 $\gamma$ 和 $\beta$ 对数据的均值和方差进行进一步处理。如果不通过 $\gamma$ 和 $\beta$ 对数据进行调整，我们的数据均值为0，方差为1。这两个参数是通过反向传播学习得到的。

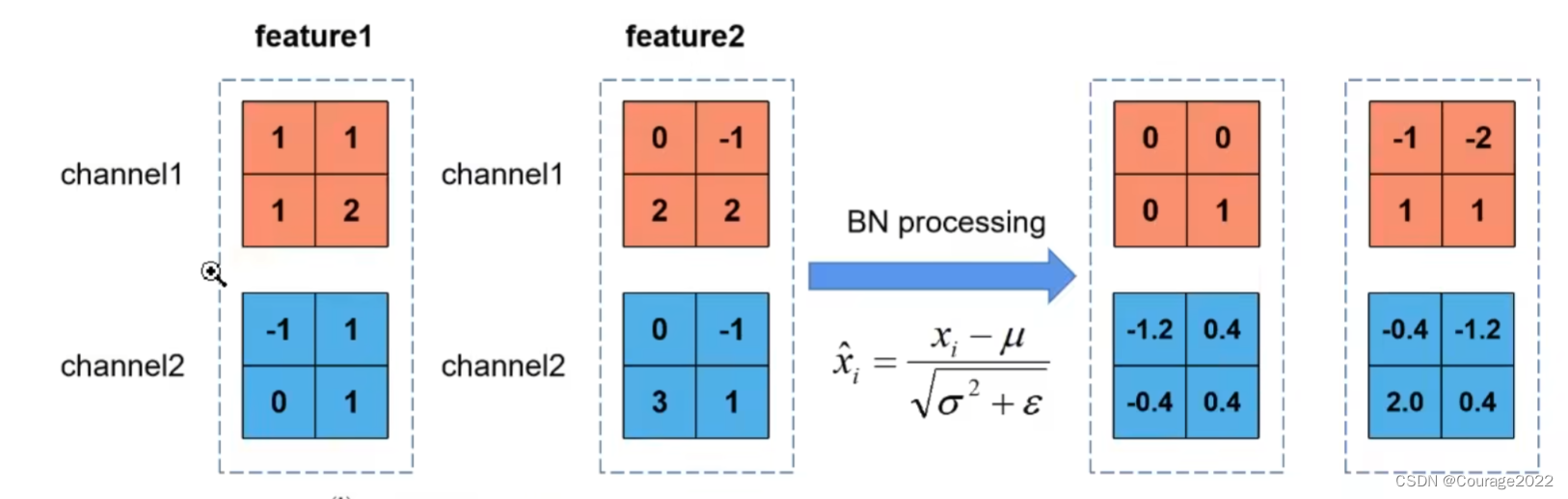
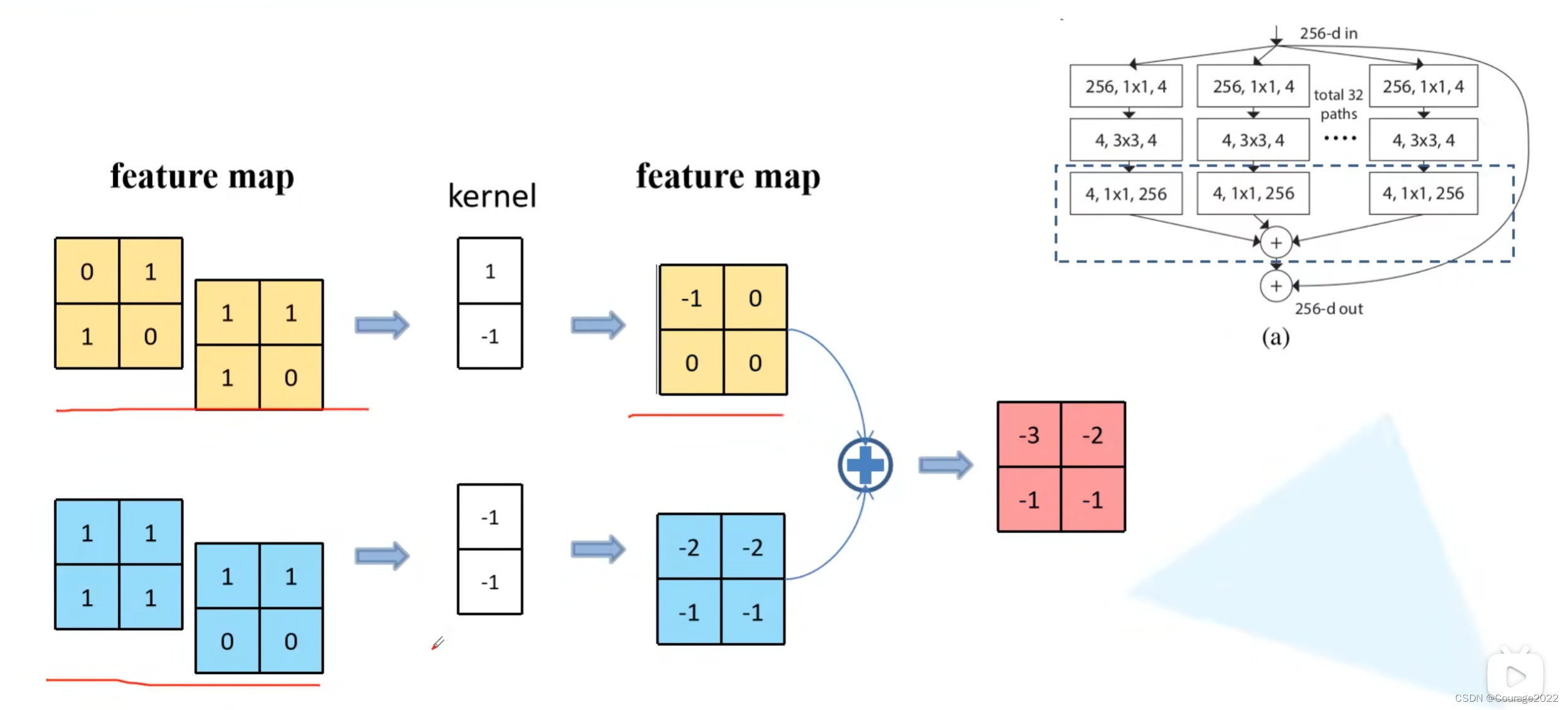
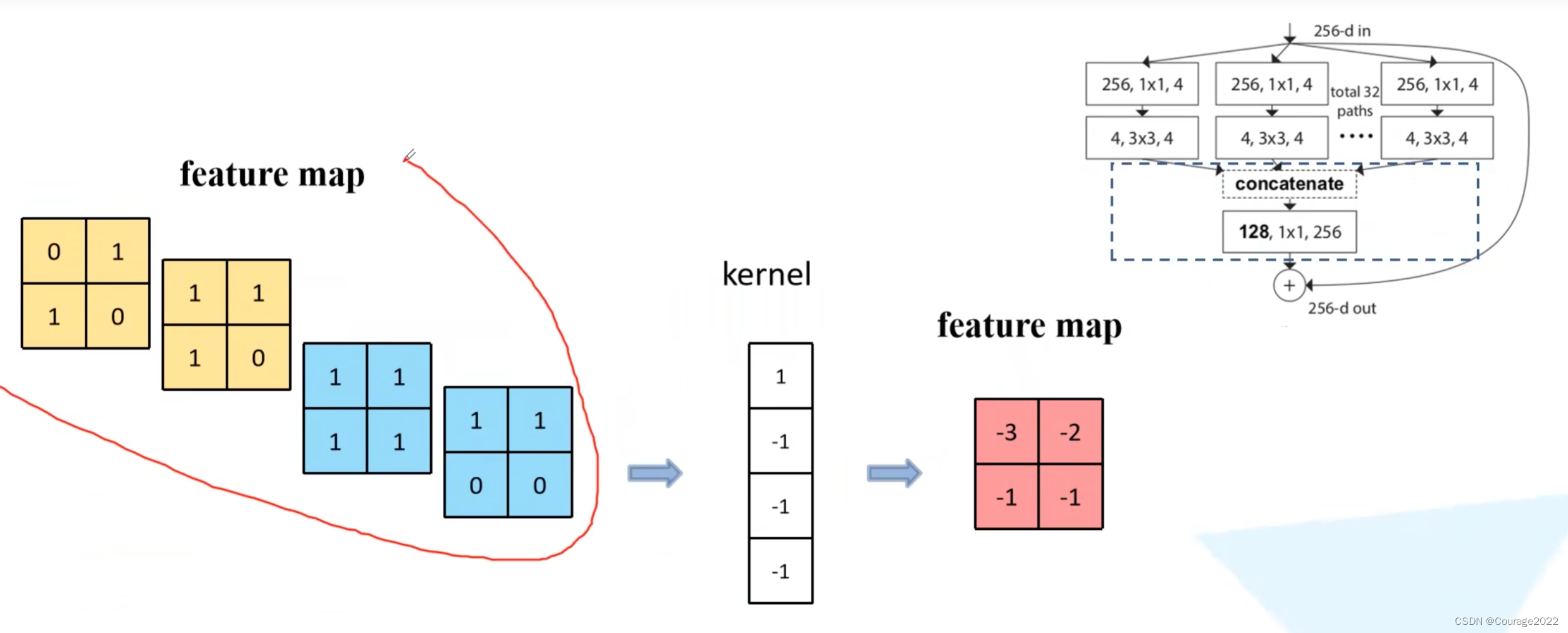
来举一个例子，假设batch_size = 2，我们这一批数据中有俩特征矩阵，我们要对这两个特征矩阵（channel = 2）进行归一化处理：

使用BN时需要注意的一些问题：

(1)训练时要将traning参数设置为True，在验证时将trainning参数设置为False。在pytorch中可通过创建模型的model.train()和model.eval()方法控制。
(2) batch size尽可能设置大点，设置小后表现可能很糟糕，设置的越大求的均值和方差越接近整个训练集的均值和方差。
(3)建议将bn层放在卷积层(Conv)和激活层（例如Relu)之间，且卷积层不要使用偏置bias，因为没有用，参考下图推理，即使使用了偏置bias求出的结果也是一样的 $y_i^b = y_i$

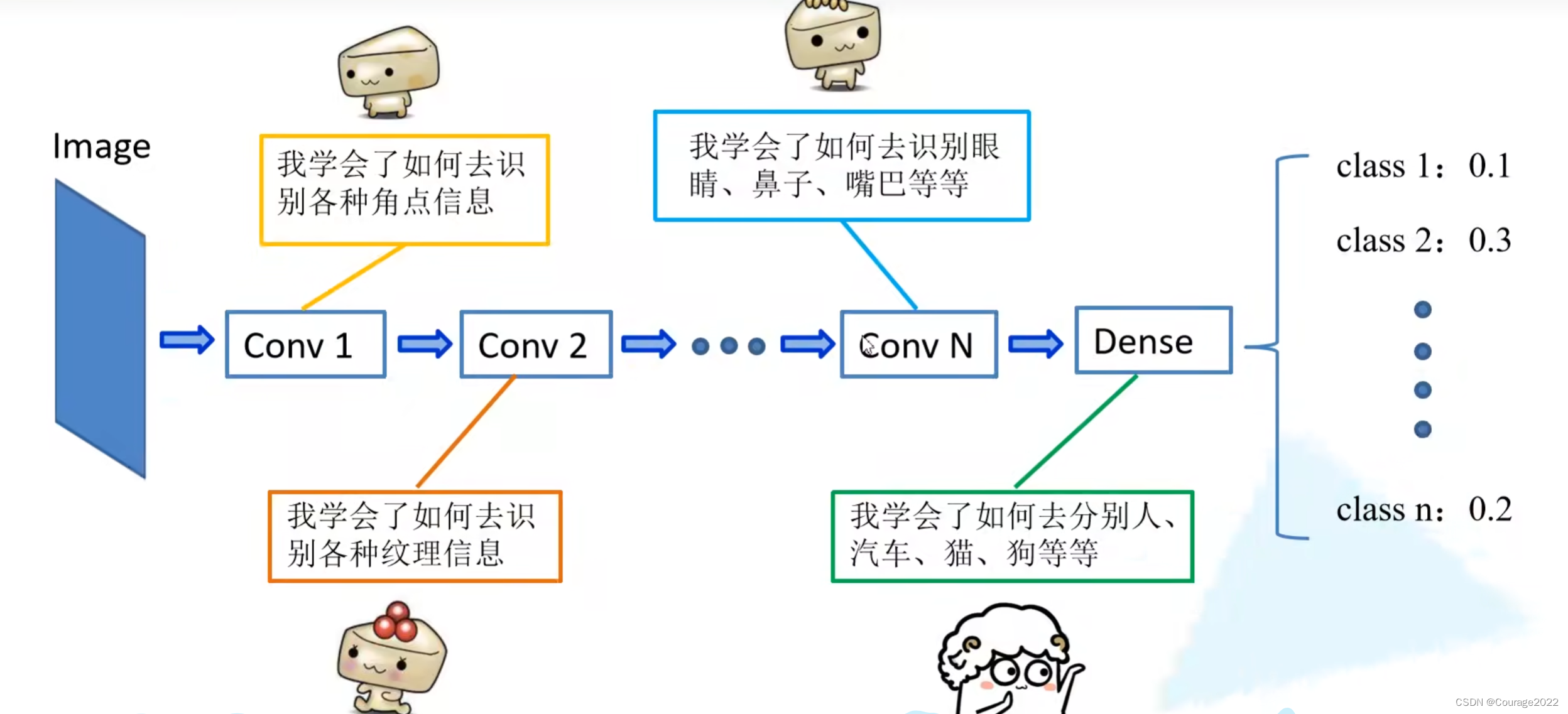
3.迁移学习

4.ResNeXt网络结构

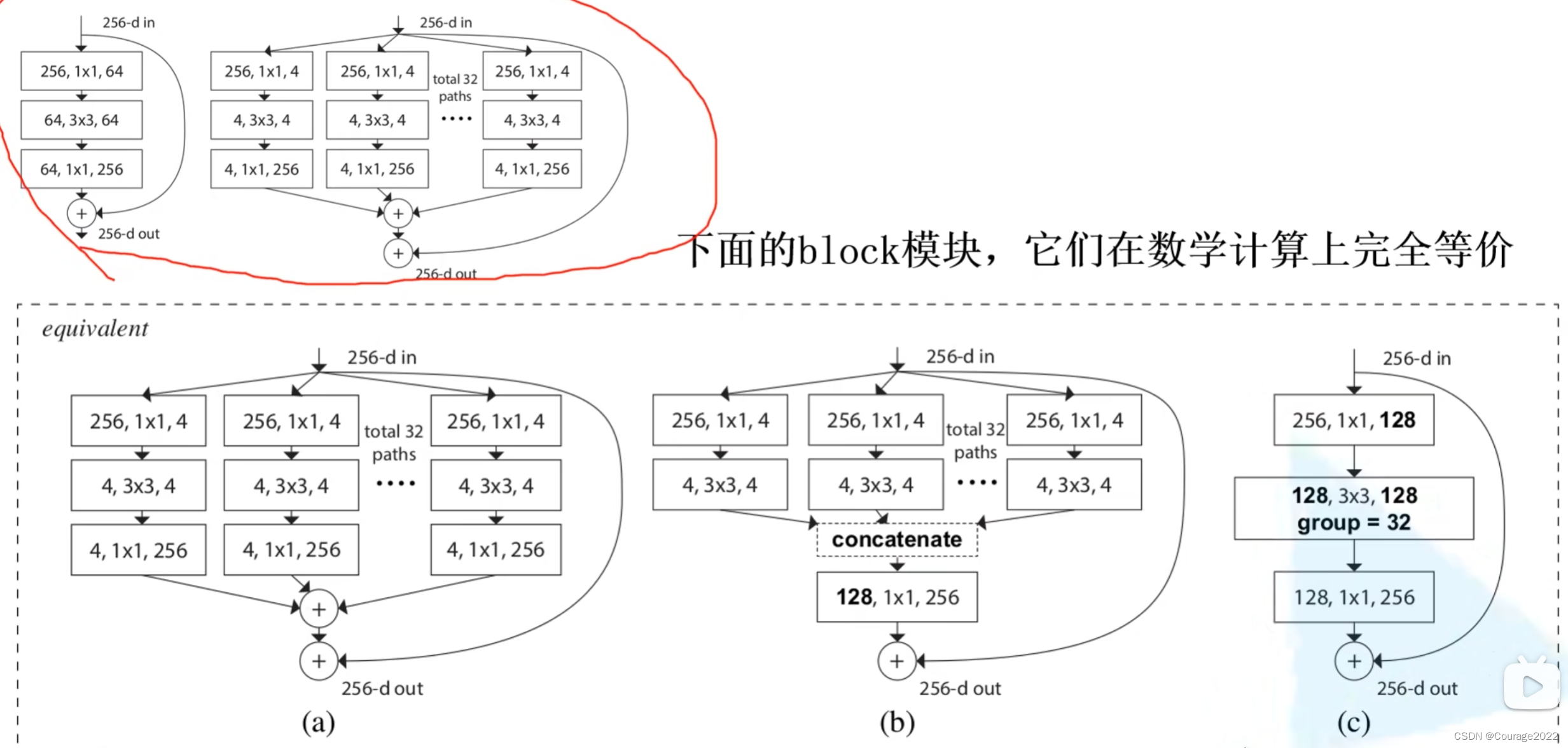
更新了残差块结构。

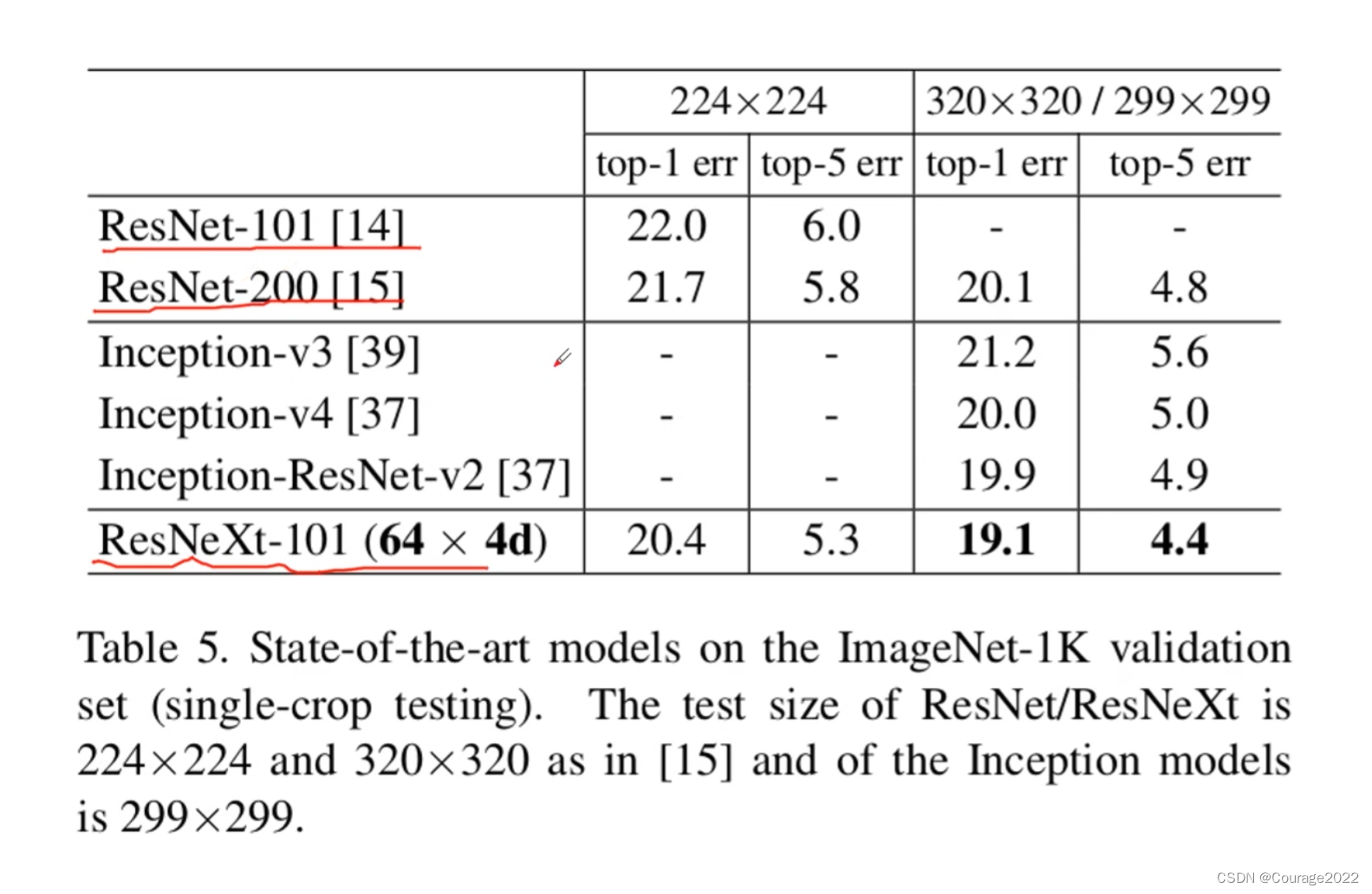
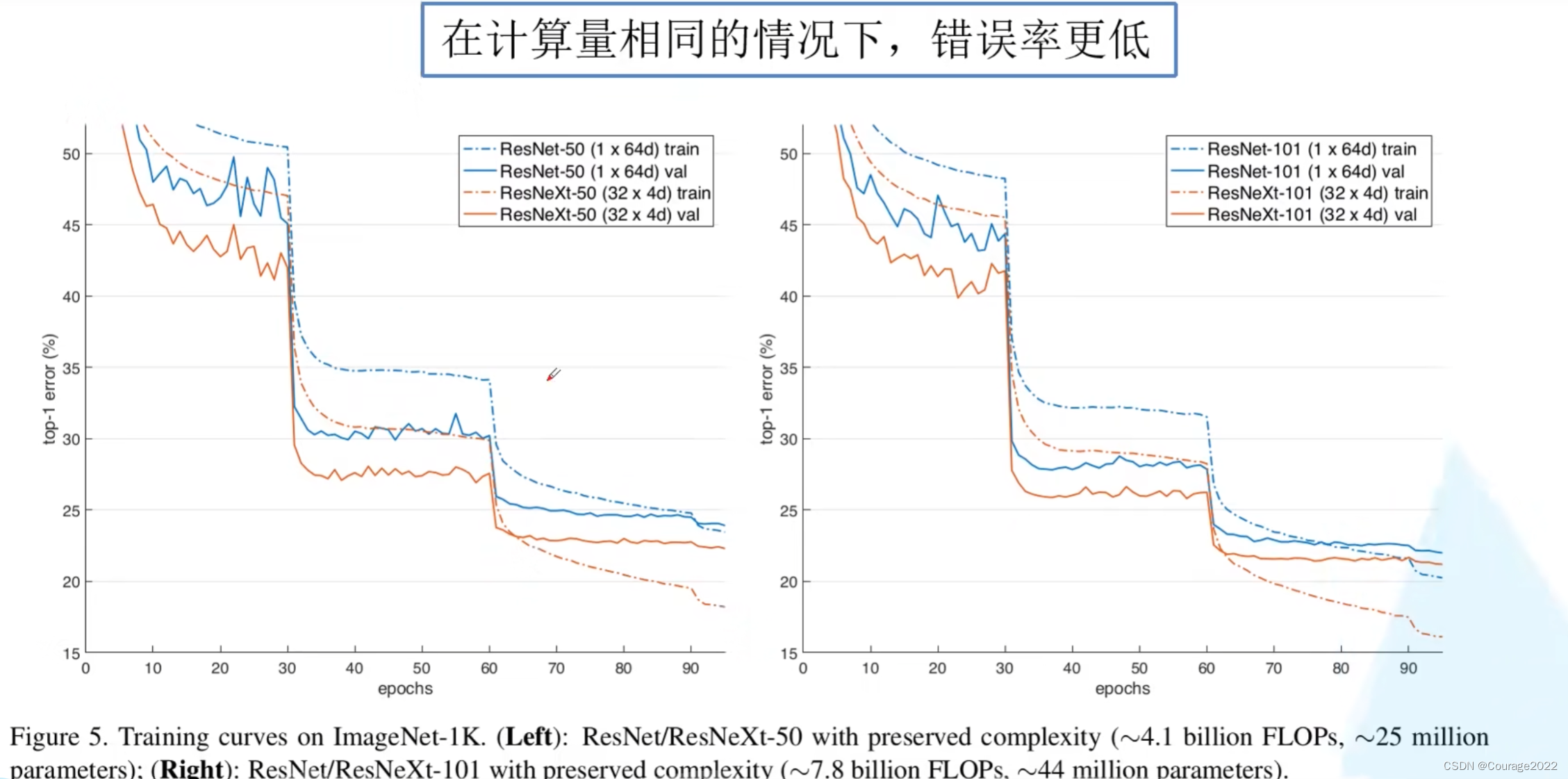
我们先看看性能参数：

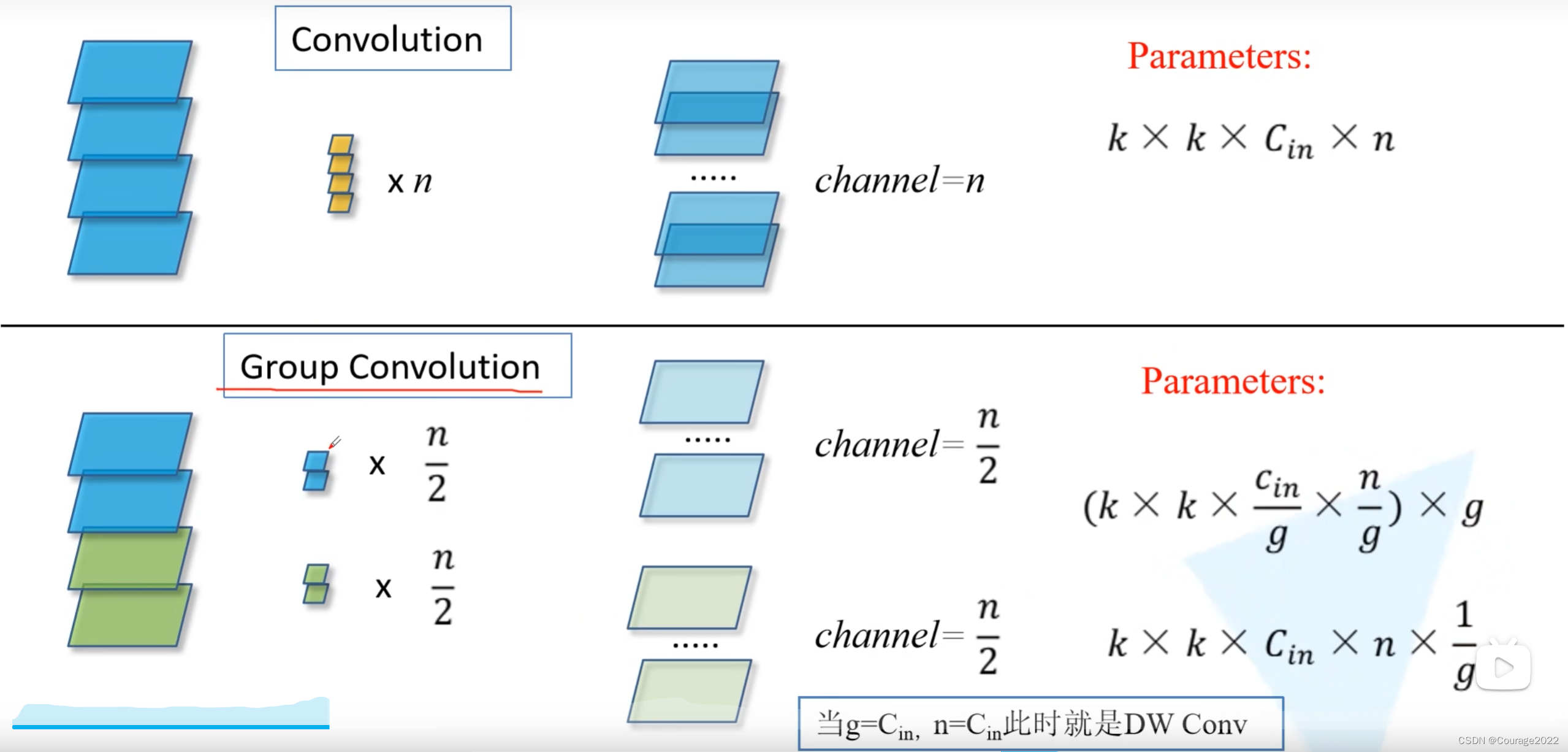
先来了解一下组卷积：

对于普通的卷积，假设输入的特征矩阵的channel = $C_{in}$ ，输出的特征矩阵channel = n，那么我们需要n个卷积核进行卷积操作，对于每一个channel都是 $k\times k$ 的图像，我们网络所需的参数数量是 $k\times k \times C_{in}\times n$ 。

对于组卷积，假设输入的特征矩阵的channel = 4，输出的特征矩阵channel 划分为两个组，对每个组分别进行卷积操作（每组的channel为 $\frac{n}{2}$ ），我们计算下组卷积的参数个数，这里还是假设每个组卷积核的高度和宽度都是等于 $k$ 的，输入特征矩阵的channel为 $C_{in}$ ，将原始特征矩阵的channel分为 $g$ 组，因此对于每个组的每个卷积核而言，它的参数个数等于 $k \times k \times \frac{C_{in}}{g}$ ，由于我们最后要得到一个channel为 $n$ 的特征矩阵，对于每个group而言，我们需要去使用 $\frac{n}{g}$ 个卷积核，划分了 $g$ 个组，最后还需乘 $g$ 。