【解法一】双栈思路梳理

【解法二】利用逆波兰表达式求解（中缀转后缀）

---

这个有俩种方法，一是直接根据条件进行各种情况的推导直接由中缀表达式求解，

                            二就是将中缀表达式转化为后缀表达式，利用更容易的逆波兰表达式求解方法

描述

        请写一个整数计算器，支持加减乘三种运算和括号。

        数据范围：0≤∣s∣≤1000≤∣s∣≤100，保证计算结果始终在整型范围内

【解法一】双栈思路梳理

最基本的就是遍历字符串给出一个访问遍历i=0；使用num栈来存放数字，使用ops栈来存放运算符

从各种情况慢慢演练：

① 当遍历为数字，那么直接入栈 也不能简单的直接将s[i]入栈，当然要连带它后面的数字进行判断，将一整个数字比如135入栈，下面源码的toInt函数哩就展示的这一功能，唯一注意点，就是需要给i取个引用，使之能通过形参的修改改变到实参。

② 当遍历为+-* 运算符时，如果ops栈为空 入ops栈（这个容易理解就不举例子了）

                                     我当前遍历符号的优先级大于栈顶元素优先级，那么直接入栈

                                    当遍历符号优先级小于栈顶元素优先级，取出2个操作数和一个操作符运算

 

 ③ 当为左括号 直接入ops栈

④ 当为右括号时，停在这个位置，把当前栈中的所有可操作运算进行执行

                           直到遇到之前放入的左括号为止 然后把这个左括号弹出，i也继续访问下一个元素

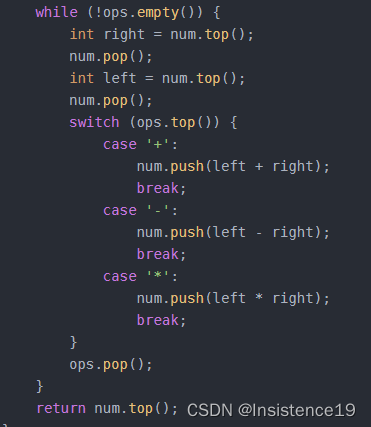
 ⑤ 当字符串s访问结束之后，还会剩余一些同级别操作符，把他们取出来依次计算即可如下：

 源码：

class Solution {
  public:
    int toInt(string s, int& i) {
        int count = 0;
        int j = i;
        while (s[i] >= '0' && s[i] <= '9') {
            i++;
            count++;
        }
        string temp = (s.substr(j, count));
        return atoi(temp.c_str());
    }
    int solve(string s) {
        // write code here
        map<char, int> mp;
        mp['-'] = 1;
        mp['+'] = 1;
        mp['*'] = 2;
        mp['('] = 0;
        stack<int> num;
        // num.push(0);
        stack<char> ops;
        int i = 0;
        while (i < s.size()) {
            if (s[i] == '+' || s[i] == '-' || s[i] == '*') {
                if (ops.empty() || mp[s[i]] > mp[ops.top()])
                    ops.push(s[i++]);
                else {
                    int right = num.top();
                    num.pop();
                    int left = num.top();
                    num.pop();
                    switch (ops.top()) {
                        case '+':
                            num.push(left + right);
                            break;
                        case '-':
                            num.push(left - right);
                            break;
                        case '*':
                            num.push(left * right);
                            break;
                    }
                    ops.pop();
                    ops.push(s[i++]);
                }
            } else if (s[i] == '(') {
                ops.push(s[i++]);
            } else if (s[i] == ')') {
                while (ops.top() != '(') {
                    int right = num.top();
                    num.pop();
                    int left = num.top();
                    num.pop();
                    switch (ops.top()) {
                        case '+':
                            num.push(left + right);
                            break;
                        case '-':
                            num.push(left - right);
                            break;
                        case '*':
                            num.push(left * right);
                            break;
                    }
                    ops.pop();
                }
                ops.pop();
                i++;
            } else {
                num.push(toInt(s, i));
            }
        }
        while (!ops.empty()) {
            int right = num.top();
            num.pop();
            int left = num.top();
            num.pop();
            switch (ops.top()) {
                case '+':
                    num.push(left + right);
                    break;
                case '-':
                    num.push(left - right);
                    break;
                case '*':
                    num.push(left * right);
                    break;
            }
            ops.pop();
        }
        return num.top();
    }
};

【解法二】利用逆波兰表达式求解（中缀转后缀）

逼站2分钟视频【逆波兰 - 上（中缀表达式 转 后缀表达式）】 https://www.bilibili.com/video/BV1xp4y1r7rc/?share_source=copy_web&vd_source=fc7e83e7f96712b431615535fe32fb1b

（1）若取出的字符是操作数 (eg, 6, 3, 7 )，则分析出完整的运算数，该操作数直接送入res。
（2）若取出的字符是运算符 (eg: ( * / - ))，则将该运算符与S1栈栈顶元素比较，如果该运算符(不包括括号运算符)优先级高于S1栈栈顶运算符（包括左括号）优先级，则将该运算符进S1栈，否则，将S1栈的栈顶运算符弹出，送入res中，直至S1栈栈顶运算符（包括左括号）低于（不包括等于）该运算符优先级时停止弹出运算符，最后将该运算符送入S1栈。
（3）若取出的字符是“（”，则直接送入S1栈顶。
（4）若取出的字符是“）”，则将距离S1栈栈顶最近的“（”之间的运算符，逐个出栈，依次送入S2栈，此时抛弃“（”。
（5）重复上面的1~4步，直至处理完所有的输入字符。
（6）若取出的字符是“#”，则将S1栈内所有运算符（不包括“#”），逐个出栈，依次送入S2栈。
如果表达式结束，但栈中还有元素，将所有元素出栈，添加到后缀表达式中

源码：

#include<map>
#include<stack>
#include<string>
class solution
{
	// 中缀转后缀
public:
	string toInt(string s, int& i) {
		int count = 0;
		int j = i;
		while (s[i] >= '0' && s[i] <= '9') {
			i++;
			count++;
		}
		return string(s.substr(j, count));
	}
	string solve(string s)
	{
		map<char, int> mp;
		mp['('] = 0;
		mp['+'] = 1;
		mp['-'] = 1;
		mp['*'] = 2;
		mp['/'] = 2;
		stack<char> ops;
		string res;
		int i = 0;
		while (i < s.size())
		{
			if (s[i] == '+' || s[i] == '-' || s[i] == '*' || s[i] == '/')
			{
				if (ops.empty() || mp[s[i]] > mp[ops.top()])
					ops.push(s[i++]);
				else
				{
					while (!ops.empty() && mp[s[i]] < mp[ops.top()])
					{
						res += ops.top();
						ops.pop();
					}
					i++;
				}
			}
			else if(s[i] == '(')
				ops.push(s[i++]);
			else if (s[i] == ')')
			{
				while (ops.top()!= '(')
				{
					res += ops.top();
					ops.pop();
				}
				i++;
				ops.pop();
			}
			else
			{
				res += toInt(s, i);
			}
		}
		while (!ops.empty())
		{
			res += ops.top();
			ops.pop();
		}
		return res;
	}
};

int main()
{
	solution ss;
	cout << "请输入中缀表达式" << endl;
	string s;
	cin >> s;
	cout << "中缀表达式为：";
	fflush(stdout);
	cout<<ss.solve(s);
	return 0;
}