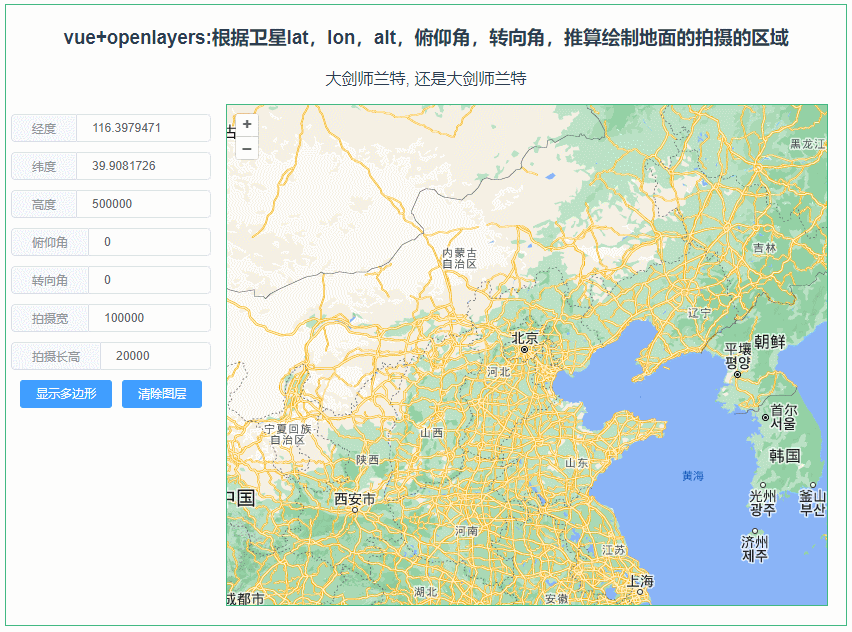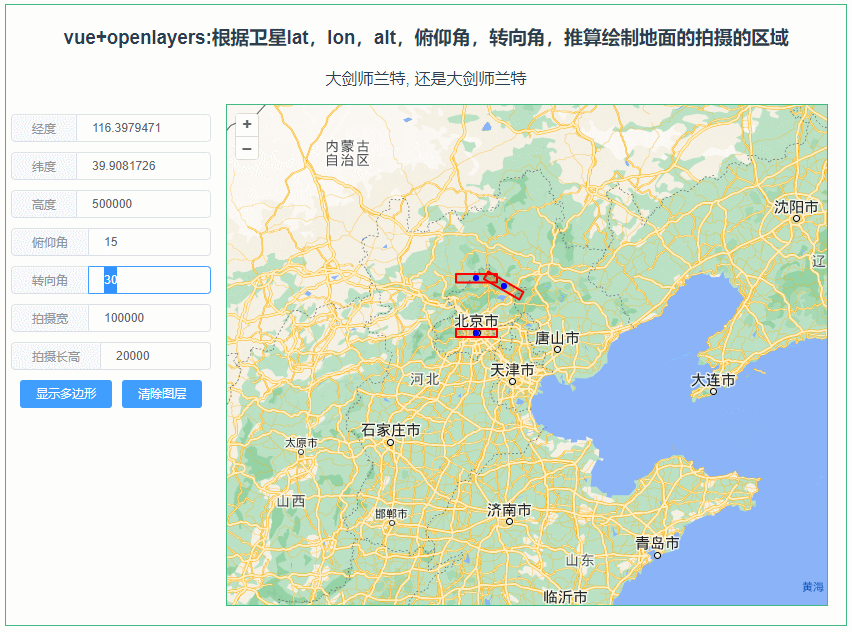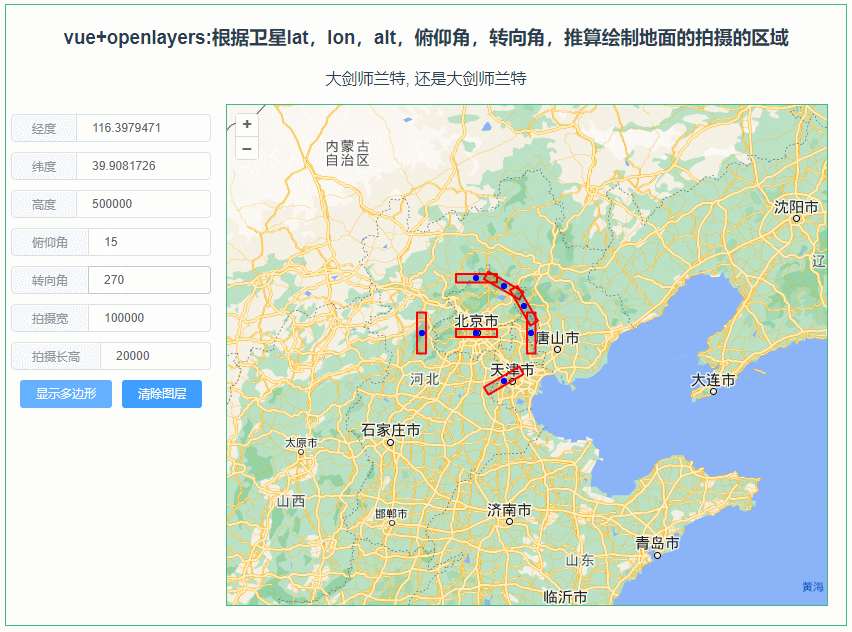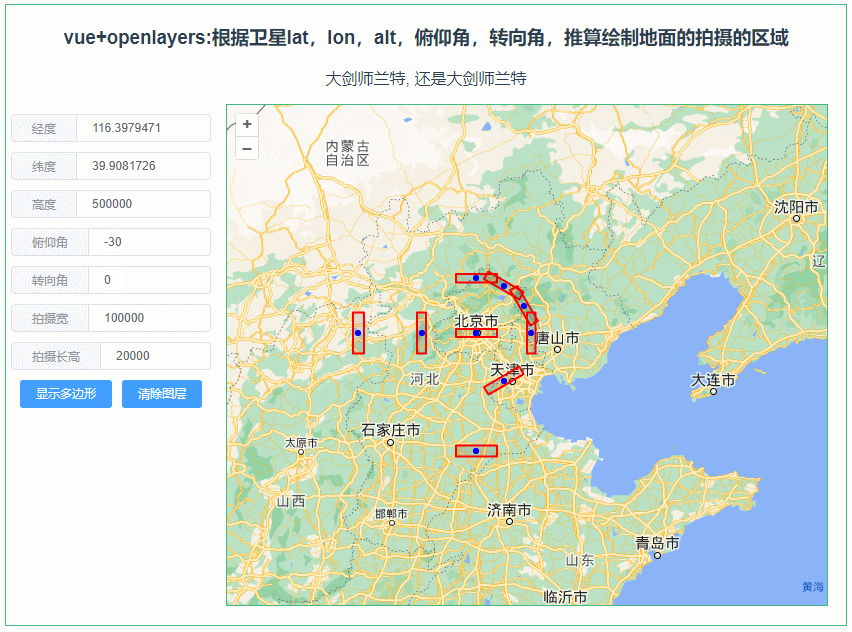
1 算法描述（凑数）

thresholdShanbhag由Robert Haase基于G.Landini和W.Rasband的工作。自动阈值器利用ImageJ中实现的Shanbhag阈值方法，使用GPU上确定的直方图创建尽可能类似于ImageJ“应用阈值”方法的二进制图像。

thresholdShanbhag By Robert Haase based on work by G. Landini and W. Rasband The automatic thresholder utilizes the Shanbhag threshold method implemented in ImageJ using a histogram determined on the GPU to create binary images as similar as possible to ImageJ ‘Apply Threshold’ method.

Method selects the algorithm to be applied (detailed below).

The Ignore black and Ignore white options set the image histogram bins for [0] and [255] greylevels to 0 respectively. This may be useful if the digitised image has under- or over- exposed pixels.

White object on black background sets to white the pixels with values above the threshold value (otherwise, it sets to white the values less or equal to the threshold).

Set Threshold instead of Threshold (single images) sets the thresholding LUT, without changing the pixel data. This works only for single images.

It you are processing a stack, two additional options are available: Stack can be used to process all the slices (the threshold of each slice will be computed separately). If this option is left unchecked, only the current slice will be processed. Use stack histogram first computes the histogram of the whole stack, then computes the threshold based on that histogram and finally binarises all the slices with that single value. Selecting this option also selects the Stack option above automatically.

Important notes:

1. This plugin is accessed through the Image › Auto Threshold menu entry, however the thresholding methods were also partially implemented in ImageJ's thresholder applet accessible through the Image › Adjust › Threshold... menu entry. While the Auto Threshold plugin can use or ignore the extremes of the image histogram (Ignore black, Ignore white) the applet cannot: the 'default' method ignores the histogram extremes but the others methods do not. This means that applying the two commands to the same image can produce apparently different results. In essence, the Auto Threshold plugin, with the correct settings, can reproduce the results of the applet, but not the way round.

2. From version 1.12 the plugin supports thresholding of 16-bit images. Since the Auto Threshold plugin processes the full greyscale space, it can be slow when dealing with 16-bit images. Note that the ImageJ thresholder applet also processes 16-bit images, but in reality ImageJ first computes a histogram with 256 bins. Therefore, there might be differences in the results obtained on 16-bit images when using the applet and the true 16-bit results obtained with this plugin. Note that for speeding up, the histogram is bracketed to include only the range of bins that contain data (and avoid processing empty histogram bins at both extremes).

3. The result of 16 bit images and stacks (when processing all slices) is an 8 bit container showing the result in white [255] to comply with the concept of "binary image" (i.e. 8 bits with 0 and 255 values). However, for stacks where only 1 slice is thresholded, the result is still a 16 bit container with the thresholded phase shown as white [65535]. This is to keep the data untouched in the remaining slices. The "Try all" option retains the 16 bit format to still show the images with methods that might fail to obtain a threshold. Images and stacks that are impossible to threshold remain unchanged.

4. The same image in 8 and 16 bits (without scaling) returns the same threshold value, however Li's method originally would return different values when the image data was offset (e.g. when adding a fixed value to all pixels). The current implementation avoids this offset-dependent problem.

5. The same image scaled by a fixed value (e.g. when multiplying all pixels by a fixed value) returns a similar threshold result (within 2 greyscale levels of the original unscaled image) for all methods except Huang, Li and Triangle due to the way these algorithms work. E.g. the Triangle method applied to an 8 bit image and to the same image converted to 16 bits with scaling can result in different threshold values. This is because the scaling from 8 to 16 bits creates empty bins in between the scaled grey values. The Triangle method (based on a geometric approach) finds those artefactual gaps in the new 16 bit histogram which satisfy the method constraints, but which would not exist in the original 8 bit image. This cannot be prevented (for example by detecting empty histogram bins) as it would interfere with the analysis when real empty bins (as oppose to artefactual ones) exist in the image.

Available methods

Try all

Which method segments your data best? One can attempt to answer this question using the Try all option. This produces a montage with results from all the methods, allowing to explore how the different algorithms perform on a particular image or stack. When using stacks, in some cases it might not be a good idea to segment each slice individually rather than with a single threshold for all slices (try the mri-stack.tif from the sample images to better understand this issue).

Error creating thumbnail: Unable to save thumbnail to destination

Original image

Error creating thumbnail: Unable to save thumbnail to destination

Try all methods.

When processing stacks with many slices, the montages can become very large (~16 times the original stack size) and one risks running out of RAM. A popup window will appear (when stacks have more than 25 slices) to confirm whether the procedure should display the montaged results. Select No to compute the threshold values and display them in the log window.

Default

This is the original method of auto thresholding available in ImageJ, which is a variation of the IsoData algorithm (described below). The Default option should return the same values as the ' Image › Adjust › Threshold › Auto', when selecting Ignore black and Ignore white. To indicate segmentation of the desired phase, use the White objects on black background option. The IsoData method is also known as iterative intermeans.

Huang

Implements Huang's fuzzy thresholding method. This uses Shannon's entropy function (one can also use Yager's entropy function).

Huang, L-K & Wang, M-J J (1995), "Image thresholding by minimizing the measure of fuzziness", Pattern Recognition 28(1): 41-51

Ported from ME Celebi's fourier_0.8 routines [1] and [2].

Huang2

This is an alternative implementation of Huang's method by J. Schindelin with an impressive speed advantage on 16 bit images. On some images, however the method gives returns different values than the original Huang method above.

Intermodes

This assumes a bimodal histogram. The histogram is iteratively smoothed using a running average of size 3, until there are only two local maxima: j and k. The threshold t is then computed as (j+k)/2. Images with histograms having extremely unequal peaks or a broad and ﬂat valley are unsuitable for this method. method

Prewitt, JMS & Mendelsohn, ML (1966), "The analysis of cell images", Annals of the New York Academy of Sciences 128: 1035-1053

Ported from Antti Niemistö's MATLAB code. See here for an excellent slide presentation and his original MATLAB code.

IsoData

Iterative procedure based on the isodata algorithm of:

Ridler, TW & Calvard, S (1978), "Picture thresholding using an iterative selection method", IEEE Transactions on Systems, Man and Cybernetics 8: 630-632

The procedure divides the image into object and background by taking an initial threshold, then the averages of the pixels at or below the threshold and pixels above are computed. The averages of those two values are computed, the threshold is incremented and the process is repeated until the threshold is larger than the composite average. That is,

threshold = (average background + average objects)/2.

Several implementations of this method exist. See the source code for further comments.

Implements Li's Minimum Cross Entropy thresholding method based on the iterative version (2nd reference below) of the algorithm.

Li, CH & Lee, CK (1993), "Minimum Cross Entropy Thresholding", Pattern Recognition 26(4): 617-625

Li, CH & Tam, PKS (1998), "An Iterative Algorithm for Minimum Cross Entropy Thresholding", Pattern Recognition Letters 18(8): 771-776

Sezgin, M & Sankur, B (2004), "Survey over Image Thresholding Techniques and Quantitative Performance Evaluation", Journal of Electronic Imaging 13(1): 146-165

Ported from ME Celebi's fourier_0.8 routines [3] and [4].

MaxEntropy

Implements Kapur-Sahoo-Wong (Maximum Entropy) thresholding method:

Kapur, JN; Sahoo, PK & Wong, ACK (1985), "A New Method for Gray-Level Picture Thresholding Using the Entropy of the Histogram", Graphical Models and Image Processing 29(3): 273-285

Ported from ME Celebi's fourier_0.8 routines [5] and [6].

Mean

Uses the mean of grey levels as the threshold. It is used by some other methods as a first guess threshold.

Glasbey, CA (1993), "An analysis of histogram-based thresholding algorithms", CVGIP: Graphical Models and Image Processing 55: 532-537

MinError(I)

An iterative implementation of Kittler and Illingworth's Minimum Error thresholding.

This implementation seems to converge more often than the original. Nevertheless, sometimes the algorithm does not converge to a solution. In that case a warning is reported to the log window and the result defaults to the initial estimate of the threshold which is computed using the Mean method. The Ignore black or Ignore white options might help to avoid this problem.

Kittler, J & Illingworth, J (1986), "Minimum error thresholding", Pattern Recognition 19: 41-47

Ported from Antti Niemistö's MATLAB code. See here for an excellent slide presentation and the original MATLAB code.

Minimum

Similarly to the Intermodes method, this assumes a bimodal histogram. The histogram is iteratively smoothed using a running average of size 3, until there are only two local maxima. The threshold t is such that yt−1 > yt <= yt+1.

Images with histograms having extremely unequal peaks or a broad and ﬂat valley are unsuitable for this method.

Prewitt, JMS & Mendelsohn, ML (1966), "The analysis of cell images", Annals of the New York Academy of Sciences 128: 1035-1053

Ported from Antti Niemistö's MATLAB code. See here for an excellent slide presentation and the original MATLAB code.

Moments

Tsai's method attempts to preserve the moments of the original image in the thresholded result.

Tsai, W (1985), "Moment-preserving thresholding: a new approach", Computer Vision, Graphics, and Image Processing 29: 377-393

Ported from ME Celebi's fourier_0.8 routines [7] and [8].

Otsu

Otsu's threshold clustering algorithm searches for the threshold that minimizes the intra-class variance, defined as a weighted sum of variances of the two classes.

Otsu, N (1979), "A threshold selection method from gray-level histograms", IEEE Trans. Sys., Man., Cyber. 9: 62-66, doi:10.1109/TSMC.1979.4310076

See also the Wikipedia article on Otsu's method.

Ported from C++ code by Jordan Bevik.

Percentile

Assumes the fraction of foreground pixels to be 0.5.

Doyle, W (1962), "Operation useful for similarity-invariant pattern recognition", Journal of the Association for Computing Machinery 9: 259-267, doi:10.1145/321119.321123

Ported from Antti Niemistö's MATLAB code. See here for an excellent slide presentation and the original MATLAB code.

RenyiEntropy

Similar to the MaxEntropy method, but using Renyi's entropy instead.

Kapur, JN; Sahoo, PK & Wong, ACK (1985), "A New Method for Gray-Level Picture Thresholding Using the Entropy of the Histogram", Graphical Models and Image Processing 29(3): 273-285

Ported from ME Celebi's fourier_0.8 routines [9] and [10].

Shanbhag

Shanbhag, Abhijit G. (1994), "Utilization of information measure as a means of image thresholding", Graph. Models Image Process. (Academic Press, Inc.) 56 (5): 414--419, ISSN 1049-9652

Ported from ME Celebi's fourier_0.8 routines [11] and [12].

Triangle

This is an implementation of the Triangle method:

Zack GW, Rogers WE, Latt SA (1977), "Automatic measurement of sister chromatid exchange frequency", J. Histochem. Cytochem. 25 (7): 741–53, PMID 70454

Modified from Johannes Schindelin's plugin Triangle_Algorithm.

See also: http://www.ph.tn.tudelft.nl/Courses/FIP/noframes/fip-Segmenta.html#Heading118

The Triangle algorithm, a geometric method, cannot tell whether the data is skewed to one side or another, but assumes a maximum peak (mode) near one end of the histogram and searches towards the other end. This causes a problem in the absence of information of the type of image to be processed, or when the maximum is not near one of the histogram extremes (resulting in two possible threshold regions between that max and the extremes). Here the algorithm was extended to find on which side of the max peak the data goes the furthest and searches for the threshold within that largest range.

Yen

Implements Yen's thresholding method from:

Yen JC, Chang FJ, Chang S (1995), "A New Criterion for Automatic Multilevel Thresholding", IEEE Trans. on Image Processing 4 (3): 370-378, ISSN 1057-7149, doi:10.1109/83.366472

Sezgin, M & Sankur, B (2004), "Survey over Image Thresholding Techniques and Quantitative Performance Evaluation", Journal of Electronic Imaging 13(1): 146-165

Ported from ME Celebi's fourier_0.8 routines [13] and [14].

2 香巴拉算法（ Shanbhag Thresholding）的C#源代码

二值算法综述请阅读：

C#，图像二值化（01）——二值化算法综述与二十三种算法目录

https://blog.csdn.net/beijinghorn/article/details/128425225?spm=1001.2014.3001.5502

支持函数请阅读：

C#，图像二值化（02）——用于图像二值化处理的一些基本图像处理函数之C#源代码

https://blog.csdn.net/beijinghorn/article/details/128425984?spm=1001.2014.3001.5502


namespace Legalsoft.Truffer.ImageTools
{
    public static partial class BinarizationHelper
    {
 
        #region 灰度图像二值化 全局算法 Shanbhag 算法 

        /// <summary>
        /// Shanbhag算法
        /// </summary>
        /// <param name="histogram"></param>
        /// <returns></returns>
        public static int Shanbhag_Threshold(int[] histogram)
        {
            int total = Histogram_Sum(histogram);
            double[] norm_histo = Histogram_Normalize(histogram);

            double[] P1 = new double[histogram.Length];
            double[] P2 = new double[histogram.Length];
            P1[0] = norm_histo[0];
            P2[0] = 1.0 - P1[0];
            for (int i = 1; i < histogram.Length; i++)
            {
                P1[i] = P1[i - 1] + norm_histo[i];
                P2[i] = 1.0 - P1[i];
            }

            int first_bin = 0;
            for (int i = 0; i < histogram.Length; i++)
            {
                if (Math.Abs(P1[i]) > float.Epsilon)
                {
                    first_bin = i;
                    break;
                }
            }

            int last_bin = histogram.Length - 1;
            for (int i = histogram.Length - 1; i >= first_bin; i--)
            {
                if (Math.Abs(P2[i]) > float.Epsilon)
                {
                    last_bin = i;
                    break;
                }
            }

            int threshold = -1;
            double min_ent = Double.MaxValue;
            for (int it = first_bin; it <= last_bin; it++)
            {
                double ent_back = 0.0;
                double term = 0.5 / P1[it];
                for (int ih = 1; ih <= it; ih++)
                {
                    ent_back -= norm_histo[ih] * Math.Log(1.0 - term * P1[ih - 1]);
                }
                ent_back *= term;

                double ent_obj = 0.0;
                term = 0.5 / P2[it];
                for (int ih = it + 1; ih < histogram.Length; ih++)
                {
                    ent_obj -= norm_histo[ih] * Math.Log(1.0 - term * P2[ih]);
                }
                ent_obj *= term;

                double tot_ent = Math.Abs(ent_back - ent_obj);
                if (tot_ent < min_ent)
                {
                    min_ent = tot_ent;
                    threshold = it;
                }
            }
            return threshold;
        }

        public static void Shanbhag_Algorithm(byte[,] data)
        {
            int[] histogram = Gray_Histogram(data);
            int threshold = Shanbhag_Threshold(histogram);
            Threshold_Algorithm(data, threshold);
        }

        #endregion

    }
}