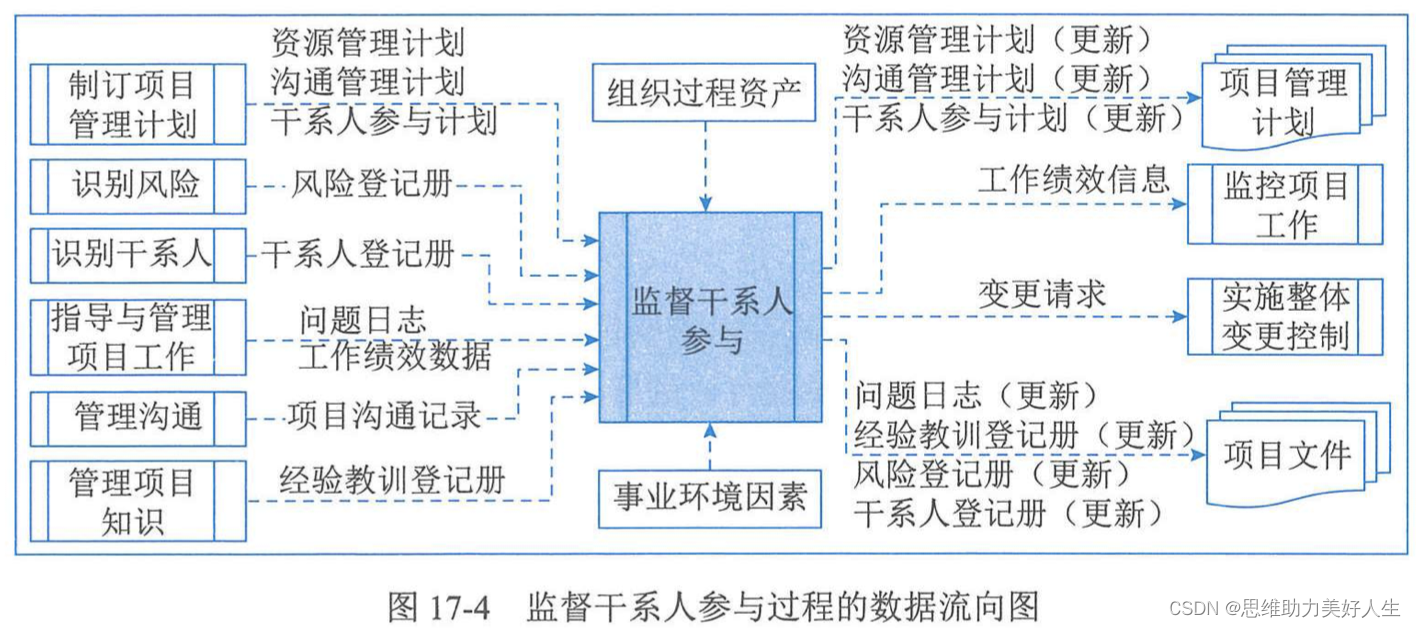
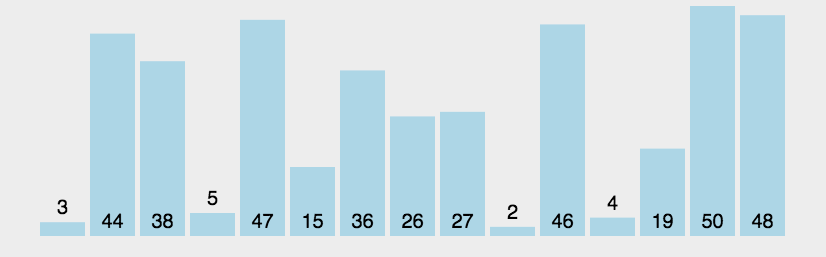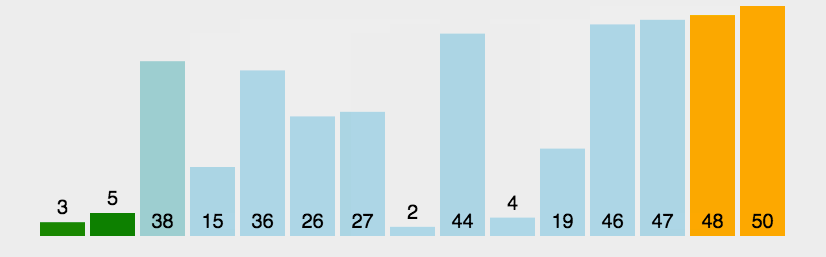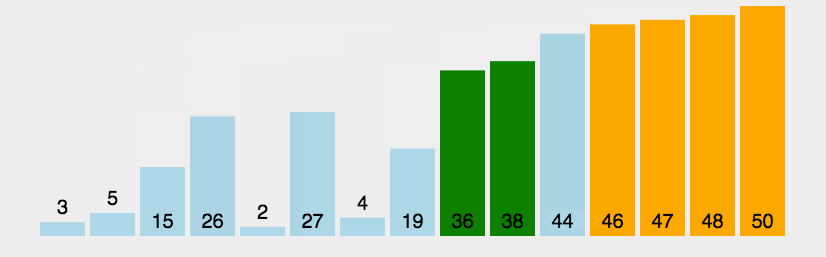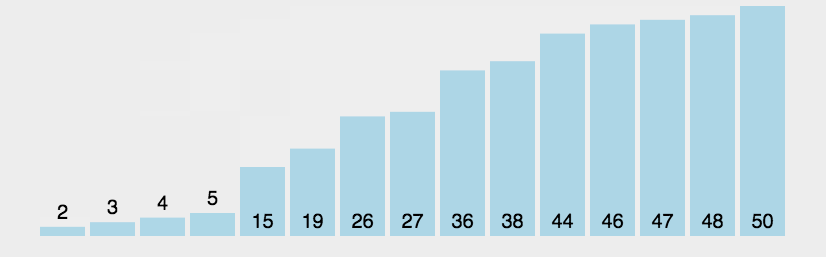题目链接

加成序列

题目描述

满足如下条件的序列 $X$（序列中元素被标号为 $1、2、3\dots m$）被称为加成序列：

1. $X[1]=1$
2. $X[m]=n$
3. $X[1]<X[2]<\dots <X[m-1]<X[m]$
4. 对于每个$k$（$2\le k\le m$）都存在两个整数$i$ 和 $j$（$1\le i,j\le k-1$，$i$ 和$j$可以相等），使得 $X[k]=X[i]+X[j]$。

你的任务是：给定一个整数$n$，找出符合上述条件的长度$m$最小的“加成序列”。

如果有多个满足要求的答案，只需要找出任意一个可行解。

输入格式

输入包含多组测试用例。
每组测试用例占据一行，包含一个整数$n$。

当输入为单行的 $0$ 时，表示输入结束。

输出格式

对于每个测试用例，输出一个满足需求的整数序列，数字之间用空格隔开。

每个输出占一行。

数据范围

$1\le n\le 100$

输入样例

5
7
12
15
77
0

输出样例

1 2 4 5
1 2 4 6 7
1 2 4 8 12
1 2 4 5 10 15
1 2 4 8 9 17 34 68 77

算法思想

题目要求输出长度最小的加成序列，由于要输出序列，因此深度优先搜索是一个不错的选择。
深度优先搜索的基本思想是每次选定一个分支，不断深入，直至到达递归边界然后回溯。这种策略带有一定的缺陷，试想当搜索树每个节点的分支数目非常多，并且问题的答案在某个较浅的节点上，如果深搜一开始选错了分支，就很可能在不包含答案的深层子树上浪费很多时间。如下图所示：

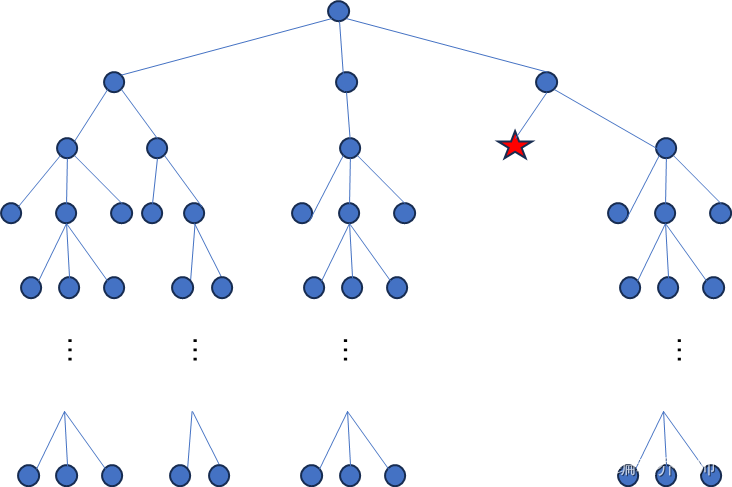
上图表示搜索的状态空间，红色五角星为答案，那么深度优先搜索算法产生的搜索树如下图所示，算法中矩形圈出的深层子树浪费了很多时间。

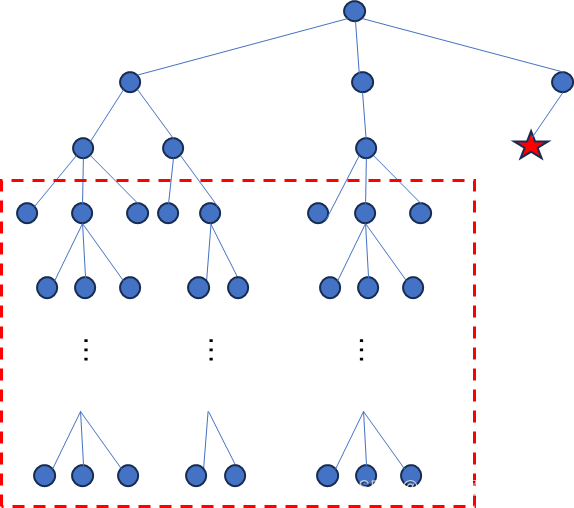
此时，可以从小到大限制搜索的深度，如果在当前深度限制下搜索不到答案，就把深度限制增加，重新进行一次搜索，这就是迭代加深思想。

所谓“迭代”，就是以上一次的结果为基础，重复执行以逼近答案的思想，迭代加深搜索的过程如下：

虽然搜索过程中深度限制为$d$时，会重复搜索$1\sim d-1$层的节点，但是当搜索树节点分支数目较多时，随着层数的深入，每层节点数会呈指数级增长，这点重复搜索与深层子树的规模相比，实在是小巫见大巫了。

总而言之，当搜索树规模随着层次的深入增长很快，并且题目能够确保答案在一个较浅层的节点时，就可使采用迭代加深的深度优先搜索算法来解决。例如，有些题目描述会包含“如果10步内搜索不到结果就算无解”的情况。

算法实现

寻找最短加成序列恰好符合迭代加深搜索的情况，序列的长度$m（m\le 10）$不会太大，但是每次枚举两个数的和产生的分支很多，即搜索树规模随着层次的深入增长很快，并且答案在一个较浅层的节点。算法实现的基本过程如下：

• 序列中的第一个数为$1$，即$X[1]=1$
• 依次搜索序列中的每个位置$k$
  • 当到达限制搜索深度时，搜索结束，如果序列中最后一个数为$n$，即$X[m]=n$，则找到最短加成序列。
  • 为了保证$X[k]=X[i]+X[j]$，枚举序列已确定的任意两个数求和，将其填入$k$位置
  • 继续搜索$k+1$位置

算法优化

• 优化搜索顺序：为了最快搜索到$n$，可以优先枚举序列中较大的数
• 排除等效冗余：对于序列中两个数的和，如果已经搜索过，就没有必要在递归搜索了，例如：$1+4$和$2+3$，其和都为$5$，搜索一次即可。

代码实现

#include <iostream>
using namespace std;
const int N = 105;
int x[N]; //加成序列
int n, m = N;
//k表示序列当前位置，d表示限制搜索深度
bool dfs(int k, int d)
{
    //达到限制搜索深度时，如果序列中最后一个元素为n，返回真，否则返回假
    if(k == d) return x[k - 1] == n; 
    bool st[N] = {0}; //通过标记，排除等效冗余，即已经搜索过的和
    //优化搜索顺序，优先选择较大的数进行求和
    for(int i = k - 1; i >= 0; i --)
    {
        for(int j = i; j >= 0; j --)
        {
            int sum = x[i] + x[j];
            if(sum <= x[k - 1] || sum > n || st[sum]) continue;
            st[sum] = true;
            x[k] = sum;
            if(dfs(k + 1, d)) return true;
        }
    }
    return false;
}
int main()
{
    x[0] = 1; // 第1个数字是1
    while(cin >> n, n)
    {
        int d = 1; //从深度1开始，迭代加深搜索，直到找到一组加成序列
        while(!dfs(1, d)) d ++;
        for(int i = 0; i < d; i ++) cout << x[i] << " ";
        cout << endl;
    }
    return 0;
}