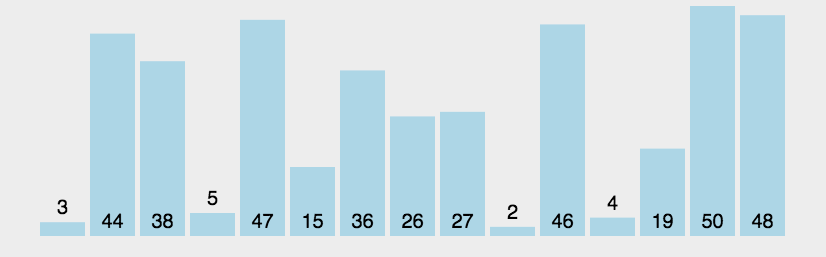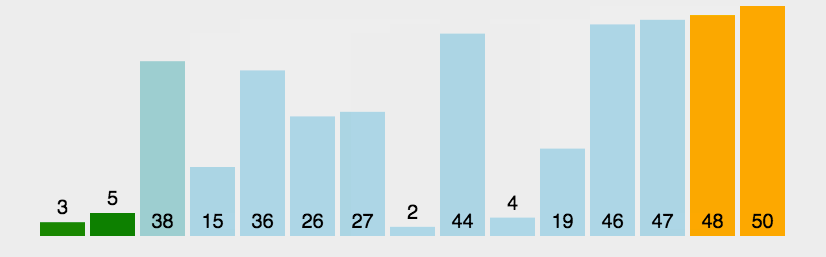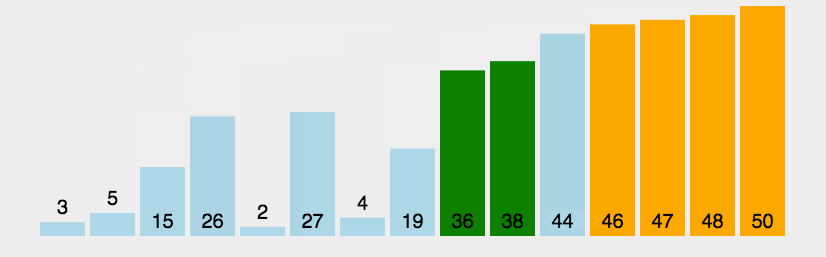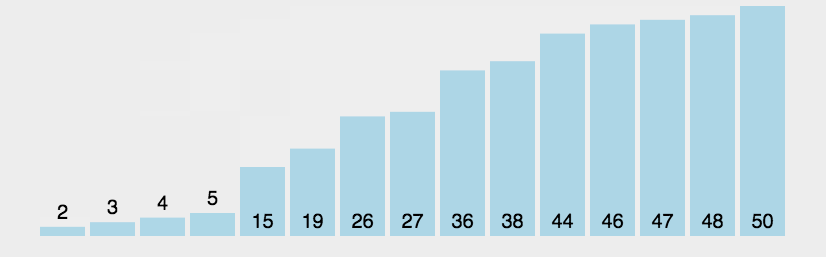1. 题目解析

题目地址：水果成篮

2. 讲解算法原理

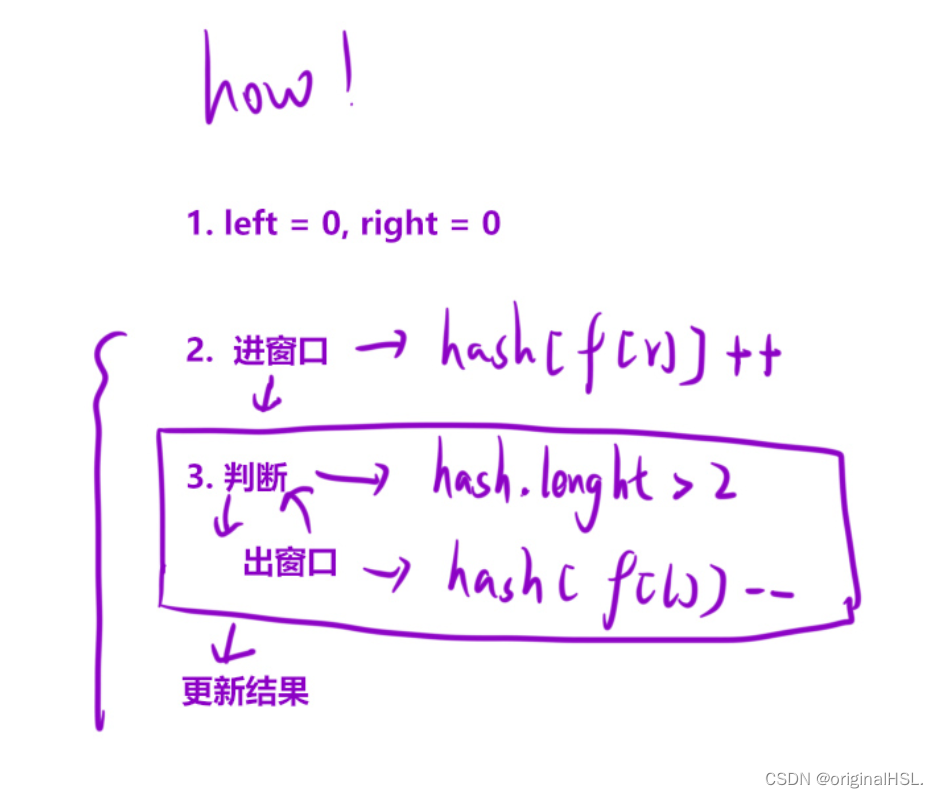
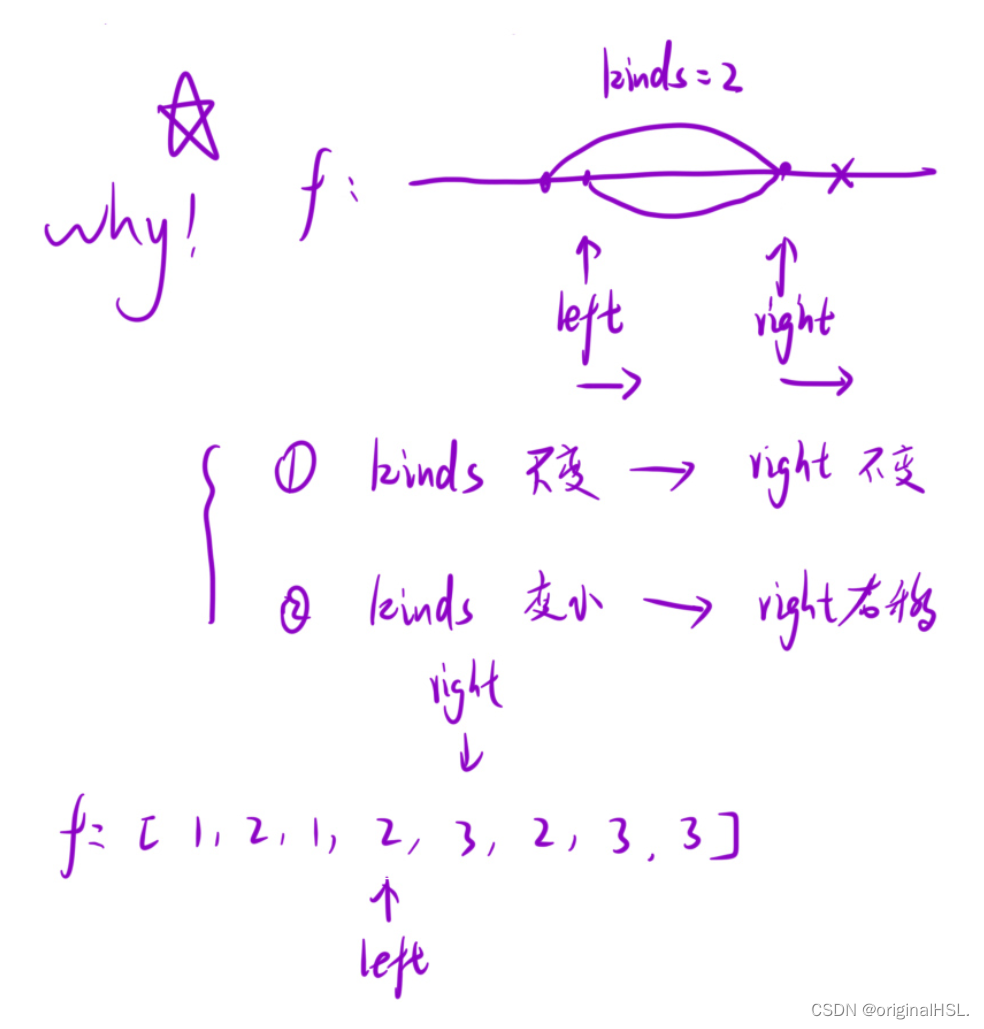
算法的主要思想是使用滑动窗口来维护一个包含最多两种水果的子数组。定义两个指针 left 和 right 分别表示窗口的左边界和右边界。还定义了一个数组 hash 来记录水果的出现次数。

算法的流程如下：

1. 初始化 left、right、len、count 为0，hash 数组的所有元素初始化为0。
2. 当 right 小于数组 fruits 的长度时，执行以下步骤：

• 如果 hash[fruits[right]] 等于0，表示当前水果在窗口内尚未出现过，将 count 增加1。
• 将 hash[fruits[right]] 的值加1，表示进入窗口。
• 当 count 大于2时，表示窗口内包含了超过两种不同的水果，需要调整窗口的左边界。
  • 将 hash[fruits[left]] 减1。
  • 如果 hash[fruits[left]] 等于0，表示左边界的水果已经全部移出窗口，将 count 减1。
  • 将 left 右移一位。
• 计算当前窗口的长度 right - left + 1，并将其与 len 中的最大值进行比较，更新 len。
• 将 right 右移一位。

3. 返回 len，即为最多只包含两种不同水果的子数组的最大长度。

---

3. 编写代码

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int hash[100001]={0};
        int left=0,right=0,len=0,count=0;
        while(right<fruits.size())
        {
            if(hash[fruits[right]]==0)
            count++;
            hash[fruits[right]]++;//进窗口
            while(count>2)//判断
            {
                hash[fruits[left]]--;   
                if(hash[fruits[left]]==0)
                {
                    count--;
                }
            left++;
            }
            len=max(len,right-left+1);
            right++;
        }   
        return len;
    }
};