以下内容有任何不理解可以翻看我之前的博客哦:吴恩达deeplearning.ai专栏
文章目录
- One-hot编码
- 连续有价值的特征
- 回归树
在之前的决策树例子中,每个分裂都只有两种选择,但是今天我们将提到一种新的分裂方式叫做One-hot,可以解决以上问题。
One-hot编码
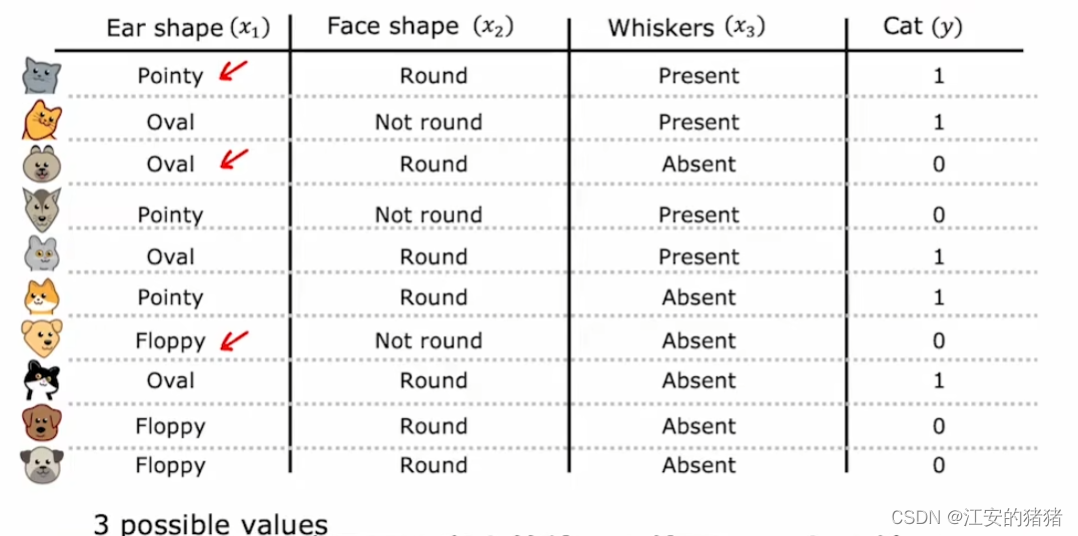
与之前的例子相比,唯一不同的是耳朵的形状,这里耳朵的形状不再只有两种可选项,这里变成了三种,圆的,尖的,椭圆的。这意味着决策树在这里可以有三个不同的分支。
在这个算法之中,我们创建了三个新的特征,第一个是是否有尖耳朵,第二个是是否有椭圆耳朵,第三个是是否有圆耳朵。很显然的是,每个猫猫狗狗只能选择这三个特征中的一个。
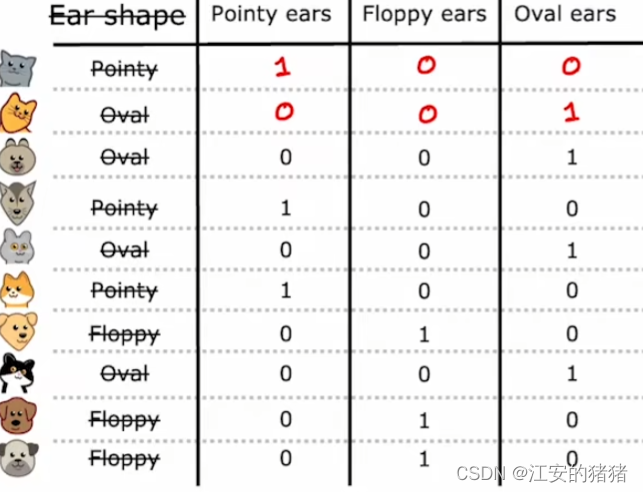
具体点说,就是**如果一个分类特征有k个能取的值,那么我们可以创建k个只能取0,1的二进制特征来替换它。**由于每次只有一个能取到1,这也是为什么它叫做one-hot。

使用one-hot算法的话,仍然可以适应以前只有两个选项的情形,只要将其中一种选择看作1,另一种看作0即可。
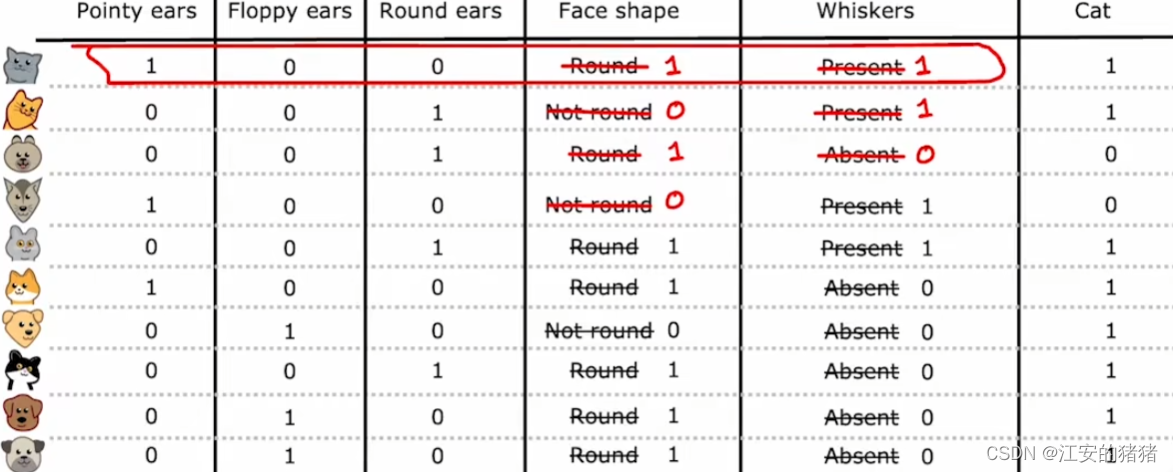
这种方式在神经网络中也可以用到。
连续有价值的特征
在学会了如何表示离散特征之后,我们再来看啊可能如何表示连续特征。
例如,我们在表格之中加入了一项体重栏,这里均是连续的数:
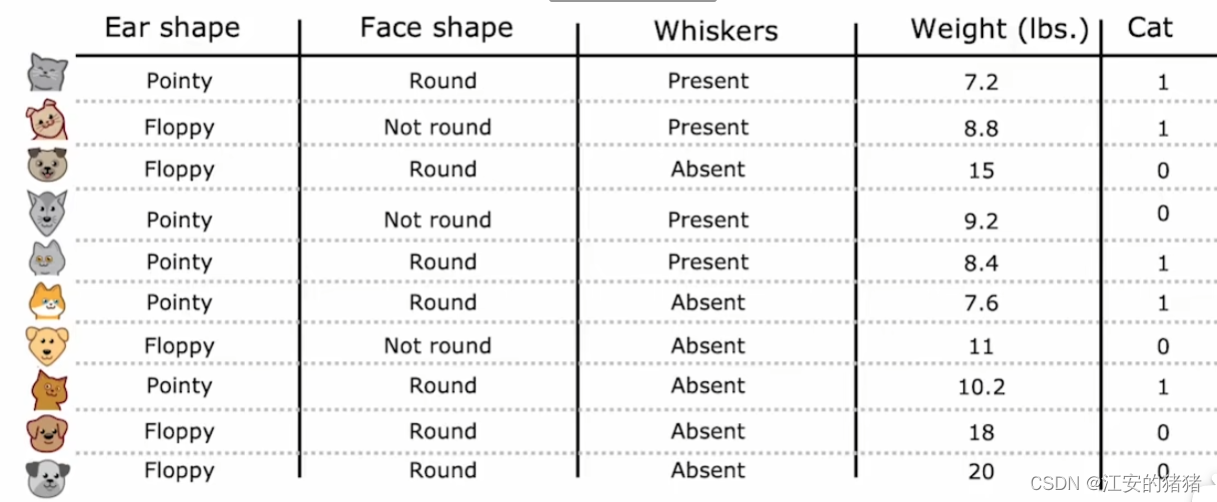
数据填写固然容易,但是它不是离散的量,我们又该如何决定分割权重特征呢?
其实很简单,你取不同的x的值作为分隔,之后看看哪种分割之后的信息增益最多。为了便于你理解,你也可以画个图:

根据公式:(这里以weight为8,蓝色线为例)
H
(
0.5
)
−
(
2
10
(
H
(
2
2
)
)
+
8
10
H
(
3
8
)
)
=
0.24
H(0.5)-(\frac{2}{10}(H(\frac{2}{2}))+\frac{8}{10}H(\frac{3}{8}))=0.24
H(0.5)−(102(H(22))+108H(83))=0.24
然后你算好几个信息增益,选择增益最大的作为分类的界限就行。
假设你发现,9kg时信息增益最大,那么:

回归树
在这个视频中,我们将决策树变为一个回归算法,从而可以让我们进行数字预测之类的问题。
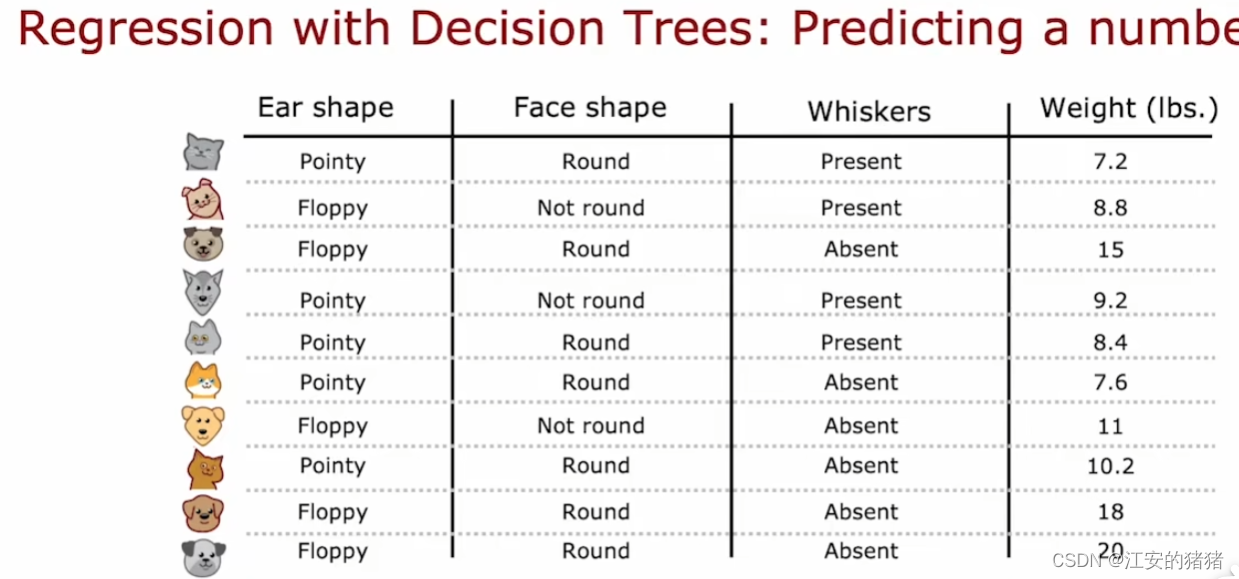
在这个例子中,我们是利用以上三个分类特征,从而来预测小动物的体重。
假设我们使用以下这种方式选择特征分类节点,我们可以计算每个叶节点的平均体重:
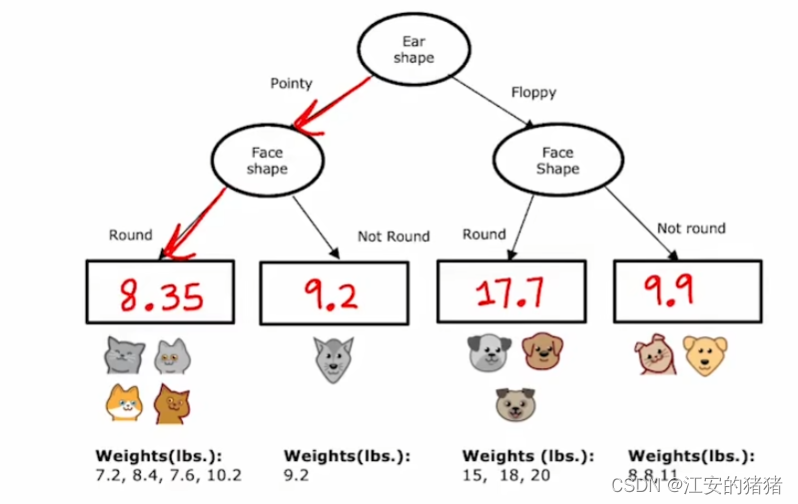
在构建回归树时,我们关注的不再是熵值,即分类的纯度,而是每个叶节点的方差,如何构建能够让各个叶节点体重的方差最小,从而可以预估到最精准的体重。
由于每个叶节点有两个值,我们采取和上面一样的方法,根据权重取平均值即可。
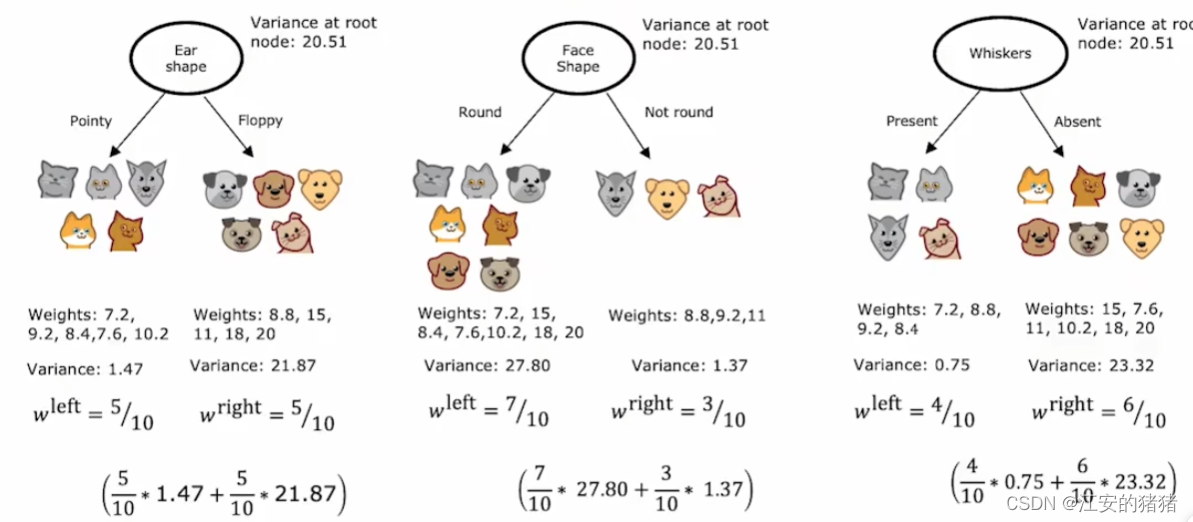
当然了,和之前类似的是,我们不光要计算方差,其实要计算的是方差的减少量,从而防止树过于臃肿反而效果不好。
如上图,减少量最多的是一号,那么就是最终选择。
为了给读者你造成不必要的麻烦,博主的所有视频都没开仅粉丝可见,如果想要阅读我的其他博客,可以点个小小的关注哦。