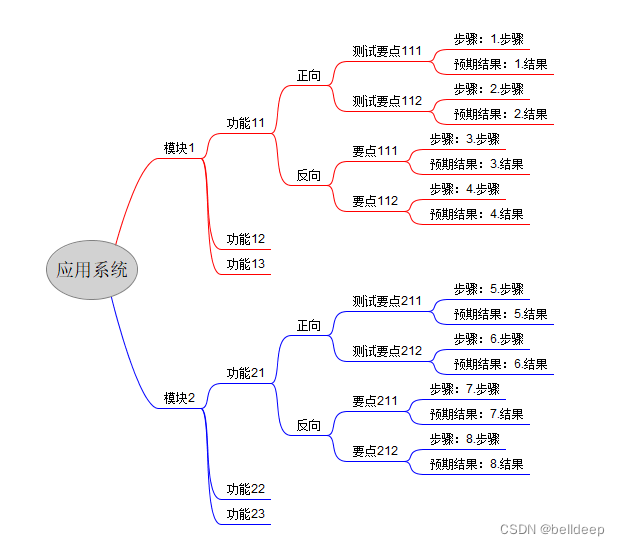
1判断完全二叉树递归做法
有四种情况:1 左树完全,右数满,且左高为右高加一
2左满 ,右满,左高为右高加一
3左满,右完全,左右高相等
4左右均满且高相等
#include<iostream>
#include<algorithm>
using namespace std;
class TreeNode {
public:
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int a) :val(a), left(nullptr), right(nullptr) {};
};
struct info {
int height;
bool iscbt;
bool isfull;
info(int a,bool b,bool c):height(a),iscbt(b),isfull(c){}
};
info process(TreeNode* head)
{
if (head == nullptr)
return info(0, true, true);
info leftinfo = process(head->left);
info rightinfo = process(head->right);
int height = max(leftinfo.height, rightinfo.height) + 1;
bool isfull = leftinfo.isfull && rightinfo.isfull && leftinfo.height == rightinfo.height;
bool iscbt = false;
if (leftinfo.isfull && rightinfo.isfull && leftinfo.height - rightinfo.height == 1)
iscbt = true;
if (leftinfo.isfull && rightinfo.isfull && leftinfo.height ==rightinfo.height )
iscbt = true;
if (leftinfo.iscbt && rightinfo.isfull && leftinfo.height - rightinfo.height == 1)
iscbt = true;
if (leftinfo.isfull && rightinfo.iscbt && leftinfo.height == rightinfo.height)
iscbt = true;
return info(height, iscbt, isfull);
}
bool iscbt(TreeNode* head)
{
if (head == nullptr)
return true;
return process(head).iscbt;
}2 给定一棵二叉树的头节点head,返回这颗二叉树中最大的二叉搜索子树的头节点
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
class TreeNode {
public:
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int data) : val(data), left(nullptr), right(nullptr) {}
};
struct info {
TreeNode* node;//最大搜索子树头结点
int maxsize;
int min;
int max;
info(TreeNode *a,int b,int c,int d):node(a),maxsize(b),min(c),max(d){}
};
info* process(TreeNode* head)
{
if (head == nullptr)
return nullptr;
info* leftinfo = process(head->left);
info* rightinfo = process(head->right);
int maxval = head->val;
int minval = head->val;
TreeNode* ans = nullptr;
int size = 0;
if (leftinfo != nullptr)
{
maxval = max(maxval, leftinfo->max);
minval = min(minval, leftinfo->min);
ans = leftinfo->node;
size = leftinfo->maxsize;
}
if (rightinfo != nullptr)
{
maxval = max(maxval, rightinfo->max);
minval = min(minval, rightinfo->min);
if (rightinfo->maxsize > size)
{
ans = rightinfo->node;
size = rightinfo->maxsize;
}
}
//当能构成搜索二叉树时
if((leftinfo==nullptr?true:(leftinfo->node==head->left&&leftinfo->max<head->val))
&& (rightinfo == nullptr ? true : (rightinfo->node == head->right && rightinfo->min > head->val)))
{
ans=head;
//一定要记得判空
size = (leftinfo == nullptr ? 0 : leftinfo->maxsize) + (rightinfo == nullptr ? 0 : leftinfo->maxsize) + 1;
}
return new info(ans, size, minval, maxval);
}
TreeNode* maxSubBSTHead2(TreeNode* head)
{
if (head == nullptr)
return nullptr;
return process(head)->node;
}
3给定一棵二叉树的头节点head,和另外两个节点a和b,返回a和b的最低公共祖先
法1:用哈希表记下所有节点父节点,将一个节点不停地向上,这其中经过的节点放入一个集合中
再在另一个节点从上遍历,一遍查找是否在集合中已经存在过,找到的第一个即为答案
#include <iostream>
#include <unordered_map>
#include <unordered_set>
using namespace std;
class TreeNode {
public:
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int data) : val(data), left(nullptr), right(nullptr) {}
};
void fillmap(TreeNode* head, unordered_map<TreeNode*, TreeNode*> &map)
{
if (head->left != nullptr)
{
map[head->left] = head;
fillmap(head->left, map);
}
if (head->right != nullptr)
{
map[head->right] = head;
fillmap(head->right, map);
}
}
TreeNode* lowestAncestor(TreeNode* head, TreeNode* p, TreeNode* q)
{
if (head == nullptr)
return nullptr;
unordered_map<TreeNode*, TreeNode*> map;//记录所有节点的父节点
map[head] = nullptr;
fillmap(head,map);
unordered_set<TreeNode*> set;
TreeNode* cur = p;
set.insert(cur);
while (map[cur] != nullptr)
{
cur = map[cur];
set.insert(cur);
}
cur = q;
while (set.find(cur) == set.end())
{
cur = map[cur];
}
return cur;
}法二:递归套路,会聚点与x有关还是无关:无关:已经在左或右树右答案,或这棵树a,b没找全
x是答案:左发现一个,右发现一个
x本身就是a,然后左右发现了b x本身就是b,左右发现a
#include <iostream>
using namespace std;
// 节点类
class Node {
public:
int value;
Node* left;
Node* right;
Node(int data) : value(data), left(nullptr), right(nullptr) {}
};
// 最低公共祖先函数
Node* lowestAncestor2(Node* head, Node* a, Node* b) {
return process(head, a, b).ans;
}
// 信息结构体
struct Info {
bool findA;
bool findB;
Node* ans;
Info(bool fA, bool fB, Node* an) : findA(fA), findB(fB), ans(an) {}
};
// 处理函数
Info process(Node* x, Node* a, Node* b) {
if (x == nullptr) {
return Info(false, false, nullptr);
}
Info leftInfo = process(x->left, a, b);
Info rightInfo = process(x->right, a, b);
bool findA = (x == a) || leftInfo.findA || rightInfo.findA;//不要忘了x本身就是a的情况
bool findB = (x == b) || leftInfo.findB || rightInfo.findB;
Node* ans = nullptr;
if (leftInfo.ans != nullptr) {
ans = leftInfo.ans;
}
else if (rightInfo.ans != nullptr) {
ans = rightInfo.ans;
}
else {
if (findA && findB) {
ans = x;
}
}
return Info(findA, findB, ans);
}
4 派对的最大快乐值
员工信息的定义如下:
class Employee {
public int happy; // 这名员工可以带来的快乐值
List<Employee> subordinates; // 这名员工有哪些直接下级
}
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树
树的头节点是公司唯一的老板,除老板之外的每个员工都有唯一的直接上级
叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外每个员工都有一个或多个直接下级
这个公司现在要办party,你可以决定哪些员工来,哪些员工不来,规则:
1.如果某个员工来了,那么这个员工的所有直接下级都不能来
2.派对的整体快乐值是所有到场员工快乐值的累加
3.你的目标是让派对的整体快乐值尽量大
给定一棵多叉树的头节点boss,请返回派对的最大快乐值。
分情况:x来,x不来,定义一个结构体,保存两个值,x来时候的最大值,x不来时候的最大值
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
struct employee {
int happy;
vector<employee*> nexts;
employee(int h):happy(h),nexts(){}
};
struct info {
int yes;
int no;
info(int a,int b):yes(a),no(b){}
};
info process(employee* head)
{
if (head == nullptr)
return info(0, 0);
int yes = head->happy;
int no = 0;
for (employee* a : head->nexts)
{
info nextinfo = process(a);
yes += nextinfo.no;
no += max(nextinfo.yes, nextinfo.no);
}
return info(yes, no);
}
int maxhappy(employee* head)
{
info allinfo = process(head);
return max(allinfo.no, allinfo.yes);
}5给定一个由字符串组成的数组strs,必须把所有的字符串拼接起来,返回所有可能的拼接结果中字典序最小的结果
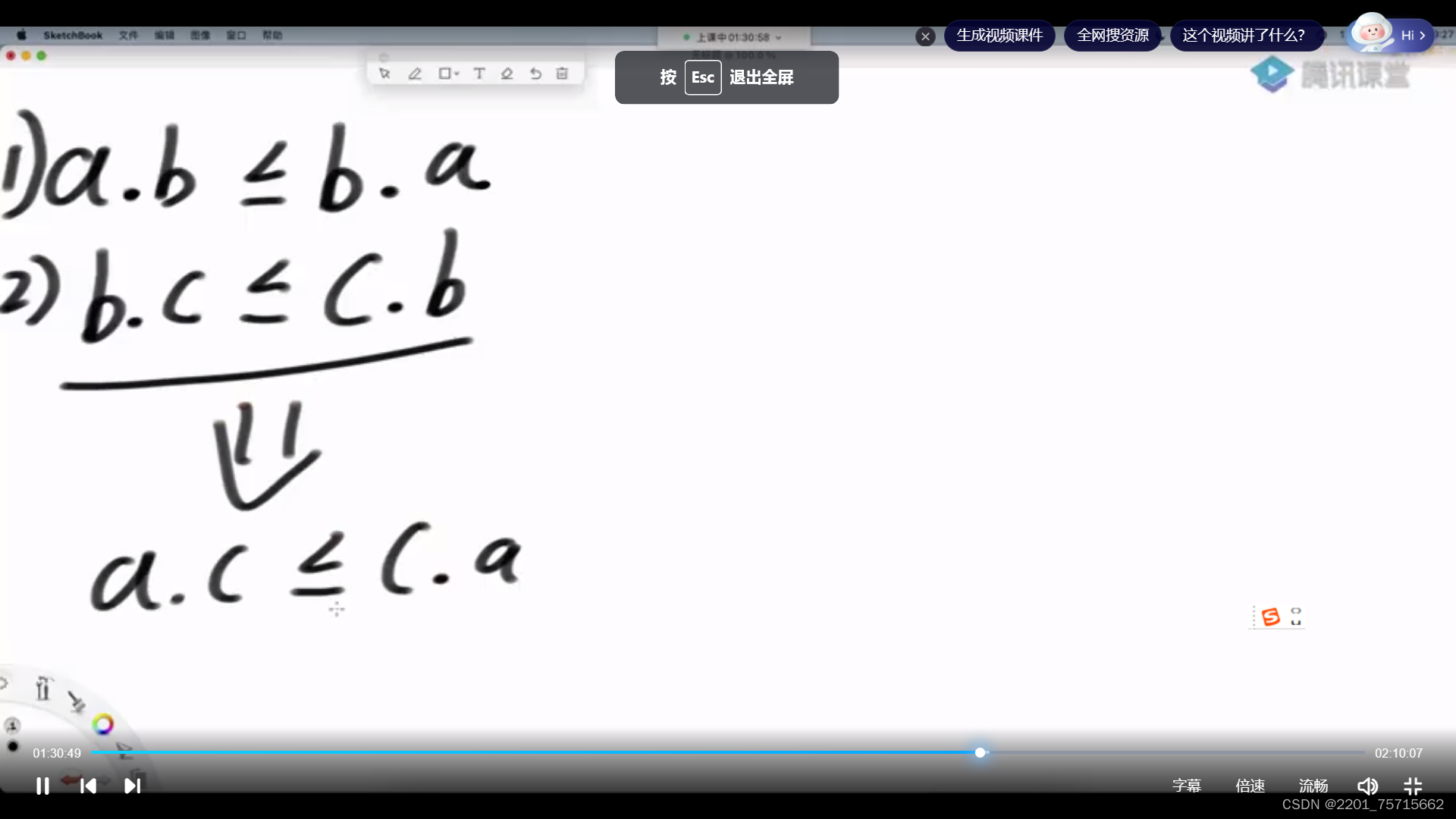
贪心:局部最小得全体最优解,有时候可能会有错
字典序:字符串排大小,长度一样比数字大小
长度不同:较短的补上最小的阿斯克码值,然后与长的比较
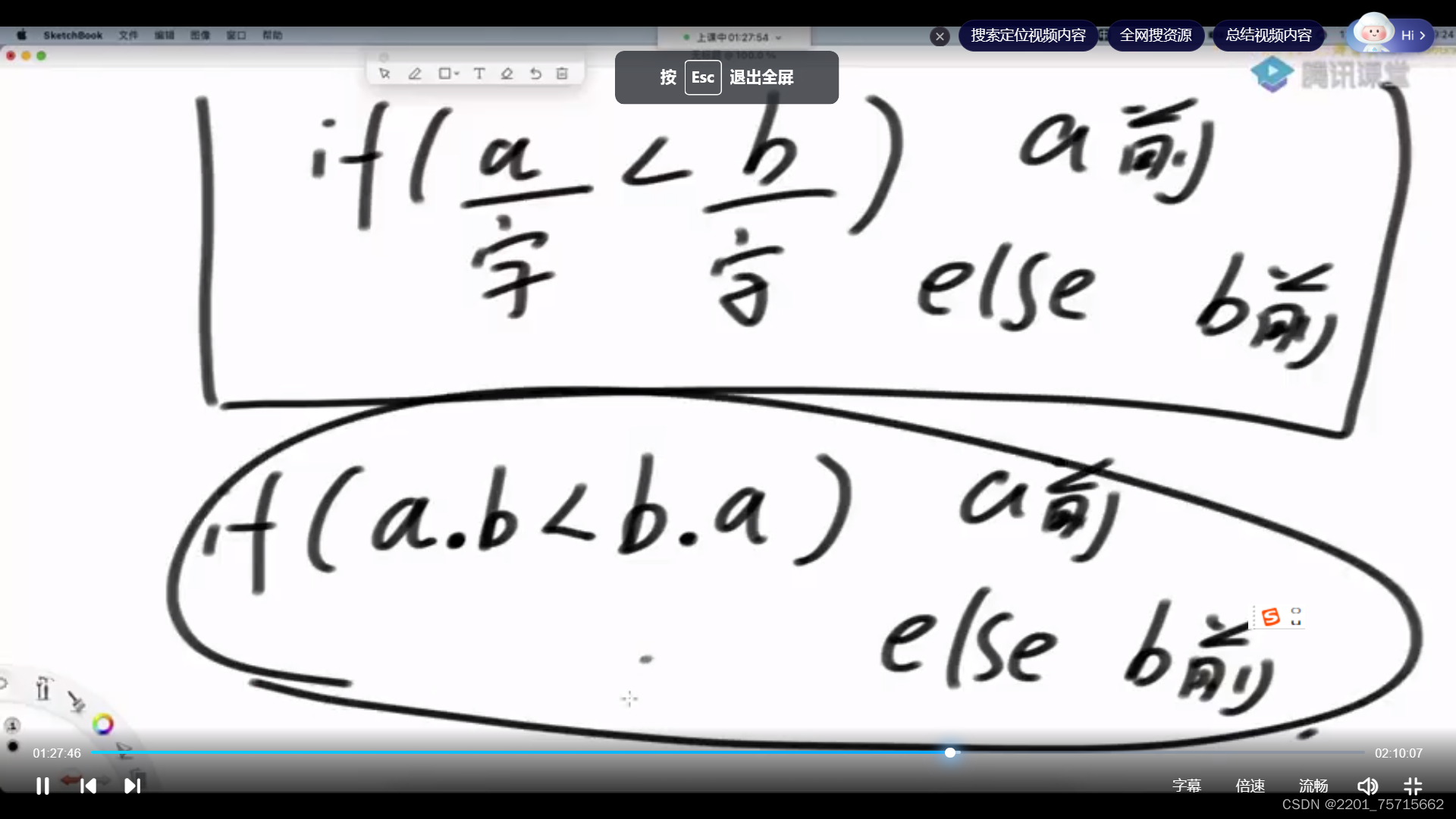
证明过程:得先证明排序过程具有传递性 ,像石头剪刀布就没有传递性
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
class compare {
public:
bool operator()(string a, string b)
{
return (a + b) < (b + a);
}
};
string lowestString(vector<string> str)
{
if (str.empty())
return "";
sort(str.begin(), str.end(), compare());
string a="";
for (string c : str)
{
a += c;
}
return a;
}

![[mmucache]-ARMV8-aarch64的虚拟内存(mmutlbcache)介绍-概念扫盲](https://img-blog.csdnimg.cn/cc002cbd5c414c5393e19c5e0a0dbf20.gif#pic_center)