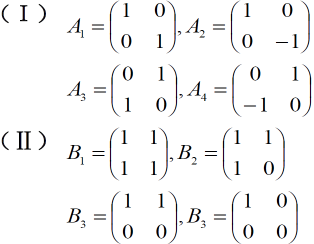一、入门操作

1、创一个tensor矩阵

x = torch.rand(5, 3)
x
out：
tensor([[0.5051, 0.7017, 0.0170],
        [0.1441, 0.2476, 0.5710],
        [0.0452, 0.8690, 0.2387],
        [0.5709, 0.0098, 0.6993],
        [0.3203, 0.5124, 0.1010]])

创建好后可以直接打印，要比tensorflow好用太多

2、矩阵大小

这跟numpy略有区别，numpy是shape

pytorch是size

x.size()

out：
torch.Size([5, 3])

3、简单计算

x=torch.rand(5,3)
y=torch.rand(5,3)

x
tensor([[0.5051, 0.7017, 0.0170],
        [0.1441, 0.2476, 0.5710],
        [0.0452, 0.8690, 0.2387],
        [0.5709, 0.0098, 0.6993],
        [0.3203, 0.5124, 0.1010]])
y
tensor([[0.6415, 0.5819, 0.3311],
        [0.0086, 0.4336, 0.5773],
        [0.3360, 0.5421, 0.1845],
        [0.4490, 0.1557, 0.5100],
        [0.0162, 0.5474, 0.3124]])

add=x + y #add=torch.add(x, y)
print(add)

out:
tensor([[1.1466, 1.2836, 0.3481],
        [0.1527, 0.6813, 1.1483],
        [0.3812, 1.4111, 0.4232],
        [1.0199, 0.1655, 1.2094],
        [0.3364, 1.0598, 0.4134]])

4、与Numpy的协同操作

tensor–numpy

a = torch.ones(5)
a
b = a.numpy()
b
out：
a:tensor([1., 1., 1., 1., 1.])
b:array([1., 1., 1., 1., 1.], dtype=float32)

numpy-- tensor

import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
b

tensor([1., 1., 1., 1., 1.], dtype=torch.float64)

二、求导原理

先定义一个x

x = torch.randn(3,4,requires_grad=True)
x
out:
tensor([[ 2.4921,  0.3292,  0.2324, -0.8859],
        [-1.3799,  1.6637, -0.5004, -0.4578],
        [-0.2573, -2.0164,  0.3258,  0.0283]], requires_grad=True)

我们看到这里多了一个参数requires_grad

所有的tensor都有.requires_grad属性，默认为False，但是可以设置成自动求导。具体方法就是在定义tensor的时候，让这个属性为True，需要注意的是，要想使x支持求导，必须让x为浮点类型

我们继续liner—regress

b = torch.randn(3,4,requires_grad=True)
b
tensor([[-0.2642,  0.3113,  0.0120, -1.3174],
        [ 0.1307,  1.8577,  0.0130,  0.3950],
        [-0.3580,  1.3666,  0.2026, -0.4438]], requires_grad=True)
t = 2*x*x + b
y = t.sum()
y

tensor(23.7106, grad_fn=<SumBackward0>)

• PyTorch里面，求导是调用**.backward()**方法。直接调用backward()方法，会计算对计算图叶节点的导数。

• 获取求得的导数，用**.grad**方法。

y.backward()

x.requires_grad, b.requires_grad, t.requires_grad

(True, True, True)

我们看到x,b,t的requires_grad都为True

x.grad

tensor([[ 9.9684,  1.3170,  0.9295, -3.5436],
        [-5.5196,  6.6548, -2.0017, -1.8311],
        [-1.0293, -8.0657,  1.3033,  0.1134]])

因为$y=2x^2+b$, y对x求导为4x

所以x.grad=4x

关于求导的过程可以参考链式法则

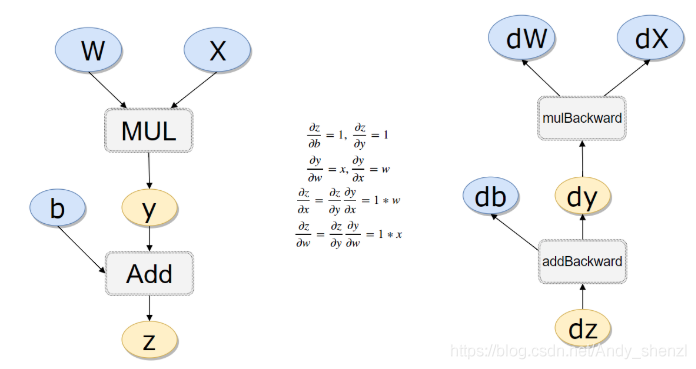
需要注意的是：求导，只能是【标量】对标量，或者【标量】对向量/矩阵求导！