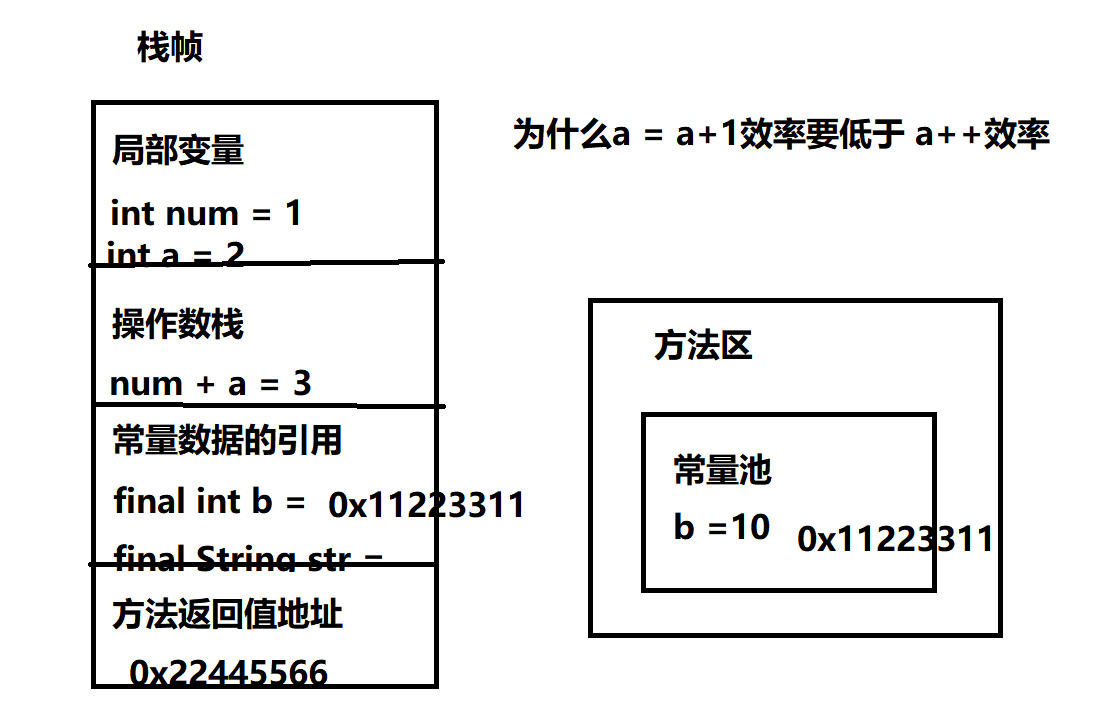
矩阵论
1. 准备知识——复数域上矩阵,Hermite变换)
1.准备知识——复数域上的内积域正交阵
1.准备知识——Hermite阵,二次型,矩阵合同,正定阵,幂0阵,幂等阵,矩阵的秩
2. 矩阵分解——SVD准备知识——奇异值
2. 矩阵分解——SVD
2. 矩阵分解——QR分解
2. 矩阵分解——正定阵分解
2. 矩阵分解——单阵谱分解
2. 矩阵分解——正规分解——正规阵
2. 矩阵分解——正规谱分解
2. 矩阵分解——高低分解
3. 矩阵函数——常见解析函数
3. 矩阵函数——谱公式,幂0与泰勒计算矩阵函数
3. 矩阵函数——矩阵函数求导
4. 矩阵运算——观察法求矩阵特征值特征向量
4. 矩阵运算——张量积
4. 矩阵运算——矩阵拉直
4.矩阵运算——广义逆——加号逆定义性质与特殊矩阵的加号逆
4. 矩阵运算——广义逆——加号逆的计算
4. 矩阵运算——广义逆——加号逆应用
4. 矩阵运算——广义逆——减号逆
5. 线性空间与线性变换——线性空间
5. 线性空间与线性变换——生成子空间
5. 线性空间与线性变换——线性映射与自然基分解,线性变换
6. 正规方程与矩阵方程求解
7. 范数理论——基本概念——向量范数与矩阵范数
7.范数理论——基本概念——矩阵范数生成向量范数&谱范不等式
7. 矩阵理论——算子范数
7.范数理论——范数估计——许尔估计&谱估计
7. 范数理论——非负/正矩阵
8. 常用矩阵总结——秩1矩阵,优阵(单位正交阵),Hermite阵
8. 常用矩阵总结——镜面阵,正定阵
8. 常用矩阵总结——单阵,正规阵,幂0阵,幂等阵,循环阵
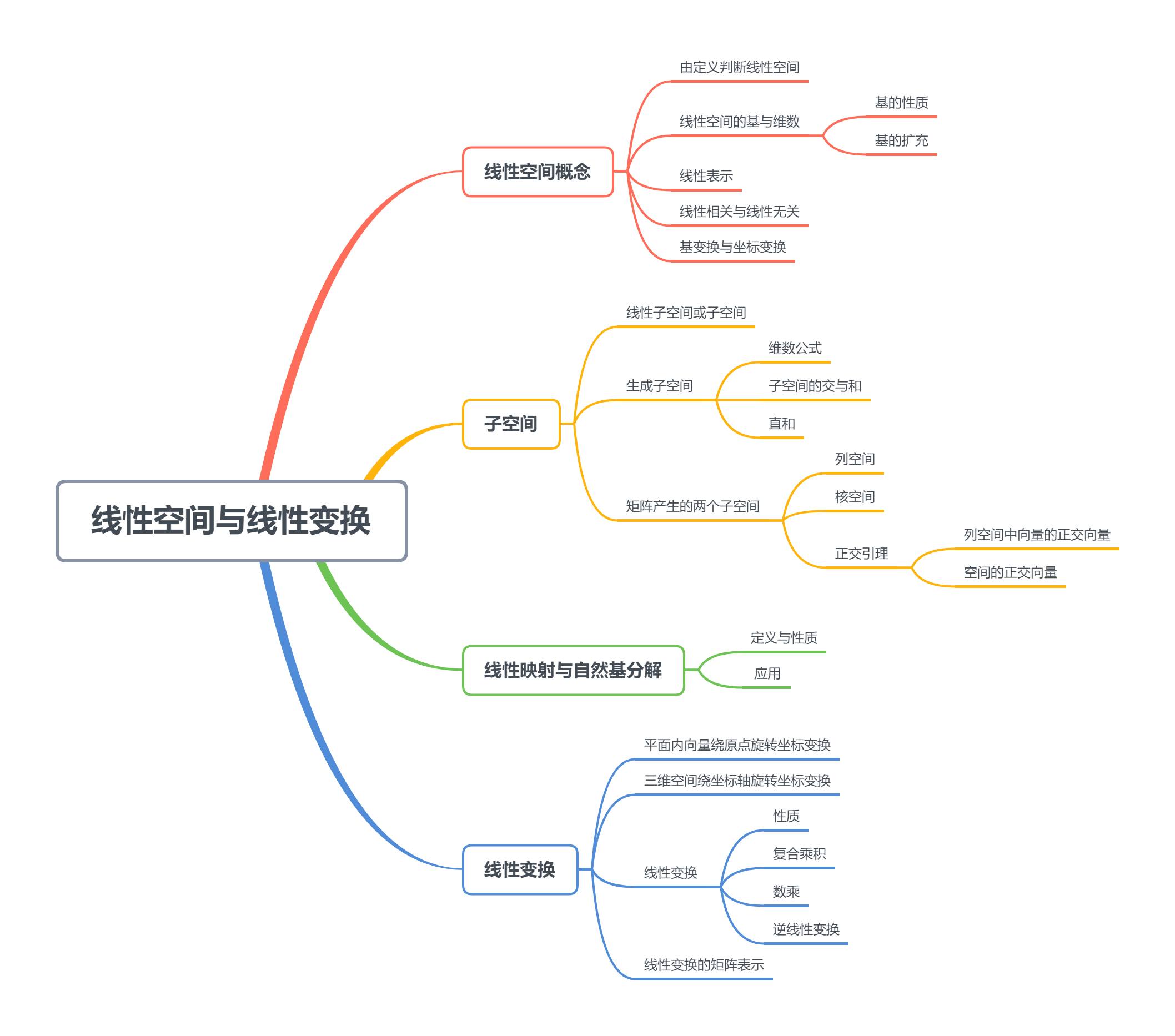
5.1 线性空间概念
5.1.1 定义与性质
数域:含0和1,且对加减乘除封闭的数集
a. 定义
设 V V V 是一个非空集合,其元素为 x , y , z x,y,z x,y,z , K K K 是一个数域,如果 V V V 中元素满足
-
V
V
V 对加法封闭,即当
x
,
y
∈
V
x,y\in V
x,y∈V 时,有唯一
x
⊕
y
∈
V
x\oplus y\in V
x⊕y∈V ,且加法满足:
- 结合律: ( x ⊕ y ) ⊕ z = x ⊕ ( y ⊕ z ) (x\oplus y)\oplus z=x\oplus (y\oplus z) (x⊕y)⊕z=x⊕(y⊕z)
- 交换律: x ⊕ y = y ⊕ x x\oplus y=y\oplus x x⊕y=y⊕x
- 存在零元素: x ⊕ 0 = x x\oplus 0=x x⊕0=x
- 存在负元素:对 ∀ x ∈ V , ∃ y ∈ V \forall x\in V,\exist y\in V ∀x∈V,∃y∈V ,使 x ⊕ y = 0 x\oplus y=0 x⊕y=0 ,则称 y y y 为 x x x 的负元素,记为 − x -x −x
-
V
V
V 对数乘运算封闭,即当
x
∈
V
,
k
∈
K
x\in V,k\in K
x∈V,k∈K 时,有唯一
k
∘
x
∈
V
k\circ x\in V
k∘x∈V ,且数乘运算满足
- 1 ∘ x = x 1\circ x=x 1∘x=x (幺元素)
- k ∘ ( x ⊕ y ) = k ∘ x ⊕ k ∘ y k\circ(x\oplus y)=k\circ x\oplus k\circ y k∘(x⊕y)=k∘x⊕k∘y
- ( k + l ) ∘ x = k ∘ x ⊕ l ∘ x (k+l)\circ x=k\circ x\oplus l\circ x (k+l)∘x=k∘x⊕l∘x
- k ∘ ( l ∘ x ) = ( k ∘ l ) ∘ x k\circ(l\circ x)=(k\circ l)\circ x k∘(l∘x)=(k∘l)∘x
则称 V V V 为数域 K K K 上的线性空间或向量空间
当 K = R K=R K=R 时,称为实线性空间
当 K = C K=C K=C 时,称为复线性空间
eg
实数域上全体 n n n 维向量的集合 R n = { ( x 1 ⋮ x n ) ∣ x 1 , ⋯ , x n ∈ R } R^n=\{\left(\begin{matrix}x_1\\\vdots\\x_n\end{matrix}\right)\vert x_1,\cdots,x_n\in R\} Rn={ x1⋮xn ∣x1,⋯,xn∈R} , α = ( x 1 x 2 ⋮ x n ) , β = ( y 1 y 2 ⋮ y n ) ∈ R n , k ∈ R \alpha=\left(\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right),\beta=\left(\begin{matrix}y_1\\y_2\\\vdots\\y_n\end{matrix}\right)\in R^n,k\in R α= x1x2⋮xn ,β= y1y2⋮yn ∈Rn,k∈R
- 加法: α + β = ( x 1 + y 1 x 2 + y 2 ⋮ x n + y n ) ∈ R n \alpha+\beta=\left(\begin{matrix}x_1+y_1\\x_2+y_2\\\vdots\\x_n+y_n\end{matrix}\right)\in R^n α+β= x1+y1x2+y2⋮xn+yn ∈Rn
- 数乘: k α = ( k x 1 k x 2 ⋮ k x n ) ∈ R n k\alpha=\left(\begin{matrix}kx_1\\kx_2\\\vdots\\kx_n\end{matrix}\right)\in R^n kα= kx1kx2⋮kxn ∈Rn
R n R^n Rn 是数域 R R R 上的线性空间
C n C^n Cn 是数域 C C C 上的线性空间
正弦函数集合 S [ x ] = { a s i n ( x + b ) ∣ a , b ∈ R } S[x]=\{asin(x+b)\vert a,b\in R\} S[x]={asin(x+b)∣a,b∈R} , s 1 , s 2 ∈ S [ x ] s_1,s_2\in S[x] s1,s2∈S[x]
-
加法
s 1 + s 2 = A 1 s i n ( x + B 1 ) + A 2 s i n ( x + B 2 ) = ( A 1 s i n B 1 c o s x + A 1 c o s B 1 s i n x ) + ( A 2 s i n B 2 c o s x + A 2 c o s B 2 s i n x ) = ( a 1 c o s x + b 1 s i n x ) + ( a 2 c o s x + b 2 s i n x ) = ( a 1 + a 2 ) c o s x + ( b 1 + b 2 ) s i n x = A s i n ( x + B ) ∈ S [ x ] \begin{aligned} s_1+s_2&=A_1sin(x+B_1)+A_2sin(x+B_2)\\ &=(A_1sinB_1cosx+A_1cosB_1sinx)+(A_2sinB_2cosx+A_2cosB_2sinx)\\ &=(a_1cosx+b_1sinx)+(a_2cosx+b_2sinx)\\ &=(a_1+a_2)cosx+(b_1+b_2)sinx\\ &=Asin(x+B)\in S[x] \end{aligned} s1+s2=A1sin(x+B1)+A2sin(x+B2)=(A1sinB1cosx+A1cosB1sinx)+(A2sinB2cosx+A2cosB2sinx)=(a1cosx+b1sinx)+(a2cosx+b2sinx)=(a1+a2)cosx+(b1+b2)sinx=Asin(x+B)∈S[x] -
数乘
λ s 1 = λ A 1 s i n ( x + B 1 ) = ( λ A 1 ) s i n ( x + B 1 ) ∈ S [ x ] \begin{aligned} \lambda s_1=\lambda A_1sin(x+B_1)=(\lambda A_1)sin(x+B_1)\in S[x] \end{aligned} λs1=λA1sin(x+B1)=(λA1)sin(x+B1)∈S[x]
∴ S [ x ] \therefore S[x] ∴S[x] 是一个线性空间
设 R + R^+ R+ 为所有正实数组成的数集,加法和数乘定义为: m ⊕ n = m n m\oplus n=mn m⊕n=mn , k ∘ m = m k k\circ m=m^k k∘m=mk ,证: R + R^+ R+ 为 R R R 上的线性空间
-
加法: a ⊕ b = a b ∈ R + a\oplus b=ab\in R^+ a⊕b=ab∈R+
a ⊕ b = a b = b a = b ⊕ a a\oplus b=ab=ba=b\oplus a a⊕b=ab=ba=b⊕a
( a ⊕ b ) ⊕ c = ( a b ) ⊕ c = a ( b c ) = a ⊕ ( b ⊕ c ) (a\oplus b)\oplus c=(ab)\oplus c=a(bc)=a\oplus(b\oplus c) (a⊕b)⊕c=(ab)⊕c=a(bc)=a⊕(b⊕c)
R + R^+ R+ 中存在零元素1, ∀ a ∈ R + \forall a\in R^+ ∀a∈R+,有 a ⊕ 1 = a ⋅ 1 = a a\oplus 1=a\cdot 1=a a⊕1=a⋅1=a
∀ a ∈ R + \forall a\in R^+ ∀a∈R+ , a ⊕ x = a ⋅ x = 1 ⇒ x = a − 1 a\oplus x=a\cdot x=1\Rightarrow x=a^{-1} a⊕x=a⋅x=1⇒x=a−1 ,即有负元素 a − 1 a^{-1} a−1
-
数乘: ∀ k ∈ R \forall k\in R ∀k∈R , k a = a k ∈ R + ka=a^k\in R^+ ka=ak∈R+
1 ∘ a = a 1 = a 1\circ a=a^1=a 1∘a=a1=a
λ ∘ ( μ ∘ a ) = λ ∘ a μ = ( a μ ) λ = a λ μ = ( λ μ ) ∘ a \lambda\circ(\mu\circ a)=\lambda\circ a^\mu=(a^{\mu})^{\lambda}=a^{\lambda\mu}=(\lambda\mu)\circ a λ∘(μ∘a)=λ∘aμ=(aμ)λ=aλμ=(λμ)∘a
( λ + μ ) ∘ a = a λ + μ = a λ a μ = a λ ⊕ a μ = λ ∘ a ⊕ μ ∘ a (\lambda+\mu)\circ a=a^{\lambda+\mu}=a^{\lambda}a^{\mu}=a^\lambda\oplus a^\mu=\lambda\circ a\oplus\mu \circ a (λ+μ)∘a=aλ+μ=aλaμ=aλ⊕aμ=λ∘a⊕μ∘a
λ ∘ ( a ⊕ b ) = λ ∘ ( a b ) = ( a b ) λ = a λ b λ = a λ ⊕ b λ = λ ∘ a ⊕ λ ∘ b \lambda\circ (a\oplus b)=\lambda\circ (ab)=(ab)^\lambda=a^\lambda b^\lambda=a^\lambda\oplus b^\lambda=\lambda\circ a\oplus \lambda\circ b λ∘(a⊕b)=λ∘(ab)=(ab)λ=aλbλ=aλ⊕bλ=λ∘a⊕λ∘b
故 R + R^+ R+ 是一个线性空间
b. 性质
线性空间 V V V 中的元素,有唯一的零元素,任意元素有唯一的负元素
证明: 假设 0 1 , 0 2 是 V 的两个零元素,由于 0 1 = 0 1 + 0 2 = 0 2 , 所以零元素唯一 设元素 x 有两个负元素 x 1 , x 2 , 由于 x 1 = x 1 + 0 = x 1 + ( x 2 + x ) = ( x 1 + x ) + x 2 = x 2 ∴ 任意元素有唯一负元素 \begin{aligned} 证明:&假设0_1,0_2是V的两个零元素,由于 0_1=0_1+0_2=0_2,所以零元素唯一\\ &设元素 x有两个负元素 x_1,x_2,由于x_1=x_1+0=x_1+(x_2+x)=(x_1+x)+x_2=x_2\\ &\therefore 任意元素有唯一负元素 \end{aligned} 证明:假设01,02是V的两个零元素,由于01=01+02=02,所以零元素唯一设元素x有两个负元素x1,x2,由于x1=x1+0=x1+(x2+x)=(x1+x)+x2=x2∴任意元素有唯一负元素
5.1.2 线性空间的基与维数
a. 线性表示
如果 x 1 , ⋯ , x m x_1,\cdots,x_m x1,⋯,xm 为线性空间 V V V 中的 m m m 个向量, x ∈ V x\in V x∈V ,且存在数域 K K K 中一组数 c 1 , ⋯ , c m c_1,\cdots,c_m c1,⋯,cm ,使 x = c 1 x 1 + ⋯ + c m x m x=c_1x_1+\cdots+c_mx_m x=c1x1+⋯+cmxm ,则称 x x x 为向量组 x 1 , ⋯ , x m x_1,\cdots,x_m x1,⋯,xm 的线性组合,即 x x x 可由 x 1 , ⋯ , x m x_1,\cdots,x_m x1,⋯,xm 线性表示
b. 线性相关与线性无关
对于 x 1 , ⋯ , x m ∈ V x_1,\cdots,x_m\in V x1,⋯,xm∈V ,如果存在不全为零的 m m m 个数 c 1 , ⋯ , c m ∈ K c_1,\cdots,c_m\in K c1,⋯,cm∈K ,使 c 1 x 1 + ⋯ + c m x m = 0 c_1x_1+\cdots+c_mx_m=0 c1x1+⋯+cmxm=0 ,则称向量组 x 1 , ⋯ , x m x_1,\cdots,x_m x1,⋯,xm 线性相关,否则为线性无关
c. 基与维数
如果 x 1 , ⋯ , x m x_1,\cdots,x_m x1,⋯,xm 是线性空间 V V V 中 m m m 个元素且满足:
- x 1 , ⋯ , x m x_1,\cdots,x_m x1,⋯,xm 线性无关
- ∀ x ∈ V \forall x\in V ∀x∈V 可由 x 1 , ⋯ , x m x_1,\cdots,x_m x1,⋯,xm 线性表示
则 x 1 , ⋯ , x m x_1,\cdots,x_m x1,⋯,xm 为 V V V 的一个基, m m m 称为 V V V 的维数,记为 d i m V = m dim V=m dimV=m
维数为 m m m 的线性空间 V V V 记为 V m V^m Vm ,当 m = + ∞ m=+\infty m=+∞ 时,称为 无限维线性空间
基性质
-
设 V V V 是 r r r 维子空间 ( d i m V = r dim V=r dimV=r) ,则 W W W 中任 r + 1 r+1 r+1 个向量必线性相关
证明: 设 V 的基为 α 1 , ⋯ , α r ,任取 β 1 , ⋯ , β r , β r + 1 ∈ V ,可知每个 β 可有 α 基向量表示,即 向量组 { β 1 , ⋯ , β r } 的秩 ≤ r ( α q , ⋯ , α r ) = r ≤ r + 1 ,故 { β } 向量组线性相关 \begin{aligned} 证明:&设V的基为 \alpha_1,\cdots,\alpha_r,任取\beta_1,\cdots,\beta_r,\beta_{r+1} \in V,可知每个\beta 可有\alpha 基向量表示,即\\ &向量组\{\beta_1,\cdots,\beta_r\}的秩\le r(\alpha_q,\cdots,\alpha_r) =r\le r+1,故\{\beta\}向量组线性相关 \end{aligned} 证明:设V的基为α1,⋯,αr,任取β1,⋯,βr,βr+1∈V,可知每个β可有α基向量表示,即向量组{β1,⋯,βr}的秩≤r(αq,⋯,αr)=r≤r+1,故{β}向量组线性相关 -
V V V 的基 [ α 1 , ⋯ , α r ] [\alpha_1,\cdots,\alpha_r] [α1,⋯,αr] 必是向量组 V V V 的一个极大无关组,从而 d i m V = r ( V ) dim V=r(V) dimV=r(V)
基的扩充
设
W
W
W 是数域
K
K
K 上的线性空间
V
n
V^n
Vn 的一个
m
m
m 维子空间,
x
1
,
⋯
,
x
m
x_1,\cdots,x_m
x1,⋯,xm 是
W
W
W 的基,则这
m
m
m 个基向量必可扩充为
V
n
V^n
Vn 的一个基
归纳法:
当
n
−
m
=
0
时,定理显然成立
假定
n
−
m
=
k
时成立,则当
n
−
m
=
k
+
1
时,由于
x
1
,
⋯
,
x
m
不是
V
n
的基
则在
V
n
中至少有一个向量
x
m
+
1
不能由
x
1
,
⋯
,
x
m
线性表示,
∴
x
1
,
⋯
,
x
m
,
x
m
+
1
线性无关
子空间
L
(
x
1
,
⋯
,
x
m
,
x
m
+
1
)
是
m
+
1
维的
∵
n
−
(
m
+
1
)
=
n
−
m
−
1
=
k
,
∴
L
(
x
1
,
⋯
,
x
m
,
x
m
+
1
)
的基
x
1
,
⋯
,
x
m
,
x
m
+
1
可以扩充为
V
n
的一个基
\begin{aligned} 归纳法:&当n-m=0时,定理显然成立\\ &假定 n-m=k时成立,则当 n-m=k+1时,由于 x_1,\cdots,x_m不是V^n的基\\ &则在V^n中至少有一个向量 x_{m+1}不能由x_1,\cdots,x_m线性表示,\therefore x_1,\cdots,x_m,x_{m+1}线性无关\\ &子空间L(x_1,\cdots,x_m,x_{m+1}) 是m+1维的\\ &\because n-(m+1)=n-m-1=k,\therefore L(x_1,\cdots,x_m,x_{m+1})的基 x_1,\cdots,x_m,x_{m+1} 可以扩充为 V^n的一个基 \end{aligned}
归纳法:当n−m=0时,定理显然成立假定n−m=k时成立,则当n−m=k+1时,由于x1,⋯,xm不是Vn的基则在Vn中至少有一个向量xm+1不能由x1,⋯,xm线性表示,∴x1,⋯,xm,xm+1线性无关子空间L(x1,⋯,xm,xm+1)是m+1维的∵n−(m+1)=n−m−1=k,∴L(x1,⋯,xm,xm+1)的基x1,⋯,xm,xm+1可以扩充为Vn的一个基
d. 坐标
设线性空间 V n V^n Vn 的一个基 x 1 , ⋯ , x n , x ∈ V n x_1,\cdots,x_n,x\in V^n x1,⋯,xn,x∈Vn , x = ξ 1 x 1 + ξ 2 x 2 + ξ n x n x=\xi_1x_1+\xi_2x_2+\xi_nx_n x=ξ1x1+ξ2x2+ξnxn ,则称 ξ 1 , ⋯ , ξ n \xi_1,\cdots,\xi_n ξ1,⋯,ξn 为 x x x 在该基下的坐标,记为 ( ξ 1 , ⋯ , ξ n ) T (\xi_1,\cdots,\xi_n)^T (ξ1,⋯,ξn)T
定理 :设 x 1 , ⋯ , x n x_1,\cdots,x_n x1,⋯,xn 是 V n V^n Vn 的一个基,且 x ∈ V n x\in V^n x∈Vn ,则 x x x 可唯一表示为 x 1 , ⋯ , x n x_1,\cdots,x_n x1,⋯,xn 的线性组合
e. 基变换与坐标变换
设
I
:
x
1
,
⋯
,
x
n
;
I
I
:
y
1
,
⋯
,
y
n
I:x_1,\cdots,x_n;II:y_1,\cdots,y_n
I:x1,⋯,xn;II:y1,⋯,yn 是
V
n
V^n
Vn 的两个基,则有:
{
y
1
=
c
11
x
1
+
c
21
x
2
+
⋯
+
c
n
1
x
n
y
2
=
c
12
x
1
+
c
22
x
2
+
⋯
+
c
n
2
x
n
⋮
y
n
=
c
1
n
x
1
+
c
2
n
x
2
+
⋯
+
c
n
n
x
n
\left\{ \begin{aligned} &y_1=c_{11}x_1+c_{21}x_2+\cdots+c_{n1}x_n\\ &y_2=c_{12}x_1+c_{22}x_2+\cdots+c_{n2}x_n\\ &\vdots\\ &y_n=c_{1n}x_1+c_{2n}x_2+\cdots+c_{nn}x_n\\ \end{aligned} \right.
⎩
⎨
⎧y1=c11x1+c21x2+⋯+cn1xny2=c12x1+c22x2+⋯+cn2xn⋮yn=c1nx1+c2nx2+⋯+cnnxn
有
(
y
1
,
⋯
,
y
n
)
=
(
x
1
,
⋯
,
x
n
)
C
(y_1,\cdots,y_n)=(x_1,\cdots,x_n)C
(y1,⋯,yn)=(x1,⋯,xn)C ,其中矩阵
C
=
(
c
11
c
12
⋯
c
1
n
c
21
c
22
⋯
c
2
n
⋮
⋮
⋱
⋮
c
n
1
c
n
2
⋯
c
n
n
)
C=\left(\begin{matrix}c_{11}&c_{12}&\cdots&c_{1n}\\c_{21}&c_{22}&\cdots&c_{2n}\\\vdots&\vdots&\ddots&\vdots\\c_{n1}&c_{n2}&\cdots&c_{nn}\end{matrix}\right)
C=
c11c21⋮cn1c12c22⋮cn2⋯⋯⋱⋯c1nc2n⋮cnn
称为基
I
I
I 到基
I
I
II
II 的过渡矩阵
对于同一向量,在不同基下有不同表示方式
x
=
(
x
1
,
⋯
,
x
n
)
(
ξ
1
⋮
ξ
n
)
=
(
y
1
,
⋯
,
y
n
)
(
η
1
⋮
η
n
)
=
(
x
1
,
⋯
,
x
n
)
C
(
η
1
⋮
η
n
)
\begin{aligned} x&=(x_1,\cdots,x_n)\left( \begin{matrix} \xi_1\\\vdots\\\xi_n \end{matrix} \right)\\ &=(y_1,\cdots,y_n)\left( \begin{matrix} \eta_1\\\vdots\\\eta_n \end{matrix} \right)=(x_1,\cdots,x_n)C\left( \begin{matrix} \eta_1\\\vdots\\\eta_n \end{matrix} \right) \end{aligned}
x=(x1,⋯,xn)
ξ1⋮ξn
=(y1,⋯,yn)
η1⋮ηn
=(x1,⋯,xn)C
η1⋮ηn
则有 坐标变换
(
ξ
1
⋮
ξ
n
)
=
C
(
η
1
⋮
η
n
)
\left(\begin{matrix}\xi_1\\\vdots\\\xi_n\end{matrix}\right)=C\left(\begin{matrix}\eta_1\\\vdots\\\eta_n\end{matrix}\right)
ξ1⋮ξn
=C
η1⋮ηn
eg
设矩阵空间 K 2 × 2 K^{2\times 2} K2×2 的两个基
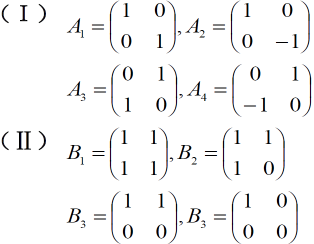
求过渡矩阵
解:
令
E
11
=
(
1
0
0
0
)
,
E
12
=
(
0
1
0
0
)
,
E
21
=
(
0
0
1
0
)
,
E
22
=
(
0
0
0
1
)
则有基变换
(
A
1
,
A
2
,
A
3
,
A
4
)
=
(
E
11
,
E
12
,
E
21
,
E
22
)
C
1
(
B
1
,
B
2
,
B
3
,
B
4
)
=
(
E
11
,
E
12
,
E
21
,
E
22
)
C
2
其中
C
1
=
(
1
1
0
0
0
0
1
1
0
0
1
−
1
1
−
1
0
0
)
,
C
2
=
(
1
1
1
1
1
1
1
0
1
1
0
0
1
0
0
0
)
∴
(
B
1
,
B
2
,
B
3
,
B
4
)
=
(
A
1
,
A
2
,
A
3
,
A
4
)
C
1
−
1
C
2
得到由基
(
I
)
到基
(
I
I
)
的过渡矩阵
C
=
C
1
−
1
C
2
=
1
2
(
2
1
1
1
0
1
1
1
2
2
1
0
0
0
1
0
)
\begin{aligned} 解:&令E_{11}=\left(\begin{matrix}1&0\\0&0\end{matrix}\right),E_{12}=\left(\begin{matrix}0&1\\0&0\end{matrix}\right),E_{21}=\left(\begin{matrix}0&0\\1&0\end{matrix}\right),E_{22}=\left(\begin{matrix}0&0\\0&1\end{matrix}\right)\\ &则有基变换 (A_1,A_2,A_3,A_4)=(E_{11},E_{12},E_{21},E_{22})C_1\\ &(B_1,B_2,B_3,B_4)=(E_{11},E_{12},E_{21},E_{22})C_2\\ &其中C_1=\left( \begin{matrix} 1&1&0&0\\0&0&1&1\\0&0&1&-1\\1&-1&0&0 \end{matrix} \right),C_2=\left( \begin{matrix} 1&1&1&1\\1&1&1&0\\1&1&0&0\\1&0&0&0 \end{matrix} \right)\\ &\therefore (B_1,B_2,B_3,B_4)=(A_1,A_2,A_3,A_4)C_1^{-1}C_2\\ &得到由基(I)到基(II)的过渡矩阵 C=C_1^{-1}C_2=\frac{1}{2}\left( \begin{matrix} 2&1&1&1\\0&1&1&1\\2&2&1&0\\0&0&1&0 \end{matrix} \right) \end{aligned}
解:令E11=(1000),E12=(0010),E21=(0100),E22=(0001)则有基变换(A1,A2,A3,A4)=(E11,E12,E21,E22)C1(B1,B2,B3,B4)=(E11,E12,E21,E22)C2其中C1=
1001100−1011001−10
,C2=
1111111011001000
∴(B1,B2,B3,B4)=(A1,A2,A3,A4)C1−1C2得到由基(I)到基(II)的过渡矩阵C=C1−1C2=21
2020112011111100