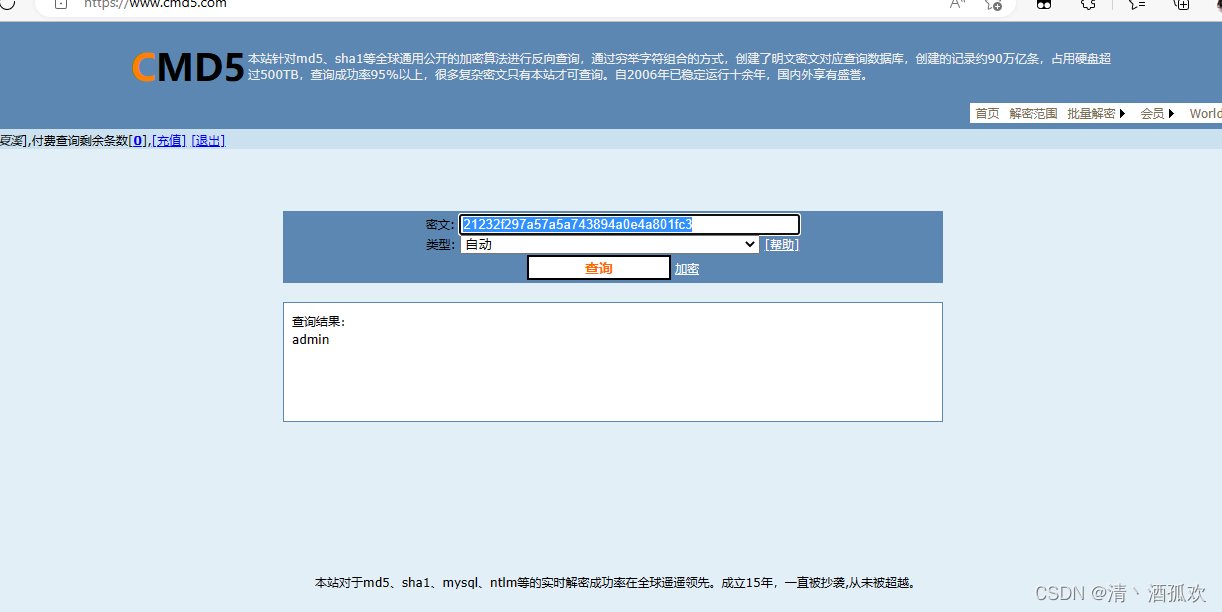
排列树

输出数组的全排列

排列问题：
    设R = {r1,r2,r3,…,rn}是要排列的n个元素，Ri = R - {r1}
    集合X中元素的全排列记为perm(X)。(ri)perm(x)便是在全排列perm(X)的每一个排列前加上前缀ri得到的排列。

    R的全排列：
        n=1时，perm(R) = (r),r是集合R中唯一的元素
        n>1时，perm(R)由(ri)perm(R1),(r2)perm(R2),…，(ri)perm(Ri)构成

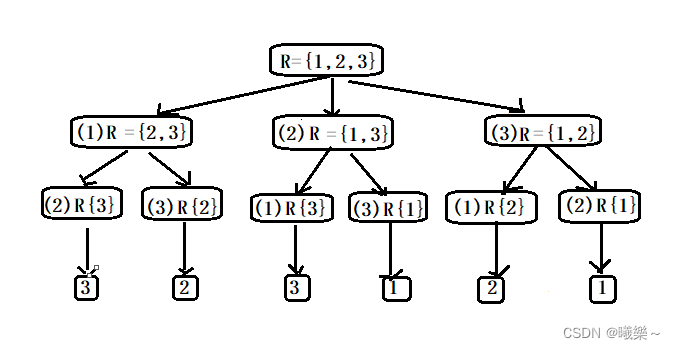
R全排列的图即为排列树（分治策略）

这种在数组中缩小规模的函数最好用两个指针，一个指向数组首，一个指向尾。

排列时将作为头的元素交换到第一个位置方便后面的数排列（如：下图中2，3排所示）

当数组中只剩一个元素时排列完成，从头输出这个排列

void Perm(int* nums, int k, int m)
{
	if (k == m)//排列完成了
	{
		for (int i = 0; i <= m; i++)
		{
			printf("%-5d", nums[i]);//输出这个排列
		}
		printf("\n");
	}
	else
	{
		for (int i = k; i <= m; i++)//i从数组的第一个走到最后一个，每一个元素都要当头一次
		{//把不变的元素换到第一位
			std::swap(nums[k], nums[i]);
			Perm(nums, k+1, m);
			//排列完换回来
			std::swap(nums[k], nums[i]);
		}
	}

}

int main()
{
	int R[] = { 1,2,3 };
	int n = sizeof(R) / sizeof(R[0]);
	Perm(R,0,n-1 );

	return 0;
}

 

---

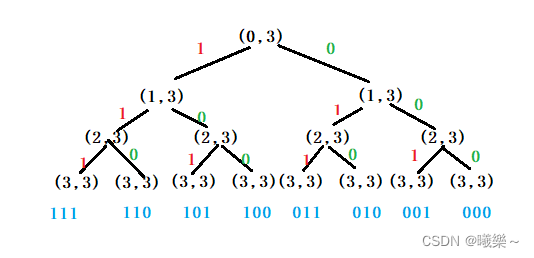
 子集树

子集树是一个满二叉树，显示数组的所有子集(1/0)，左子树为1，右子树为0，1代表取该元素，0代表不取。当规模缩至1时，输出结果。

如：int arr[] = {1,2,3}；的子集
{1,2,3}{1,2}{1,3}{2,3}{1}{2}{3}空

下图各结点代表规模（头指针位置，尾指针位置）

void func(int* arr, int* brr, int i, int n)
{
	if (i == n)//到叶子结点了
	{
		for (int j = 0; j < n; j++)
		{
			if (brr[j] == 1)//有这个元素
				printf("%-4d", arr[j]);
		}
		printf("\n");
	}
	else
	{
		//进入左子树
		brr[i] = 1;
		func(arr, brr, i + 1, n);
		//进入右子树
		brr[i] = 0;
		func(arr, brr, i + 1, n);
	}
}
int main()
{
	int arr[] = { 1,2,3 };
	int brr[] = { 0,0,0 };
	func(arr, brr, 0, 3);
}

代码深度执行，但要层次分析 ，便于画图。