目录
快速排序
实现代码
时间复杂度
快排的优化
随机选择策略
三位取中法
非递归的快排
快速排序
快速排序算法是基于分治策略的一个排序算法,其基本思想是对于输入的子数组进行分解、递归求解,最后合并。
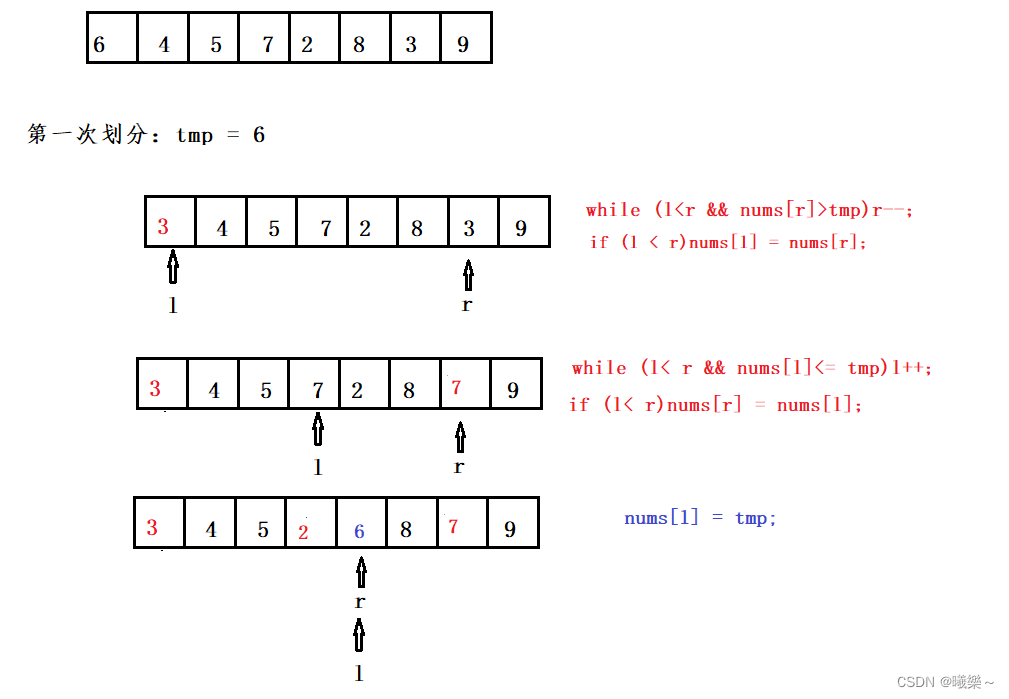
分解:以数组中左边第一个数作为基准元素,将数组划分为三段,nums[left,mid-1],nums[mid],nums[mid+1,right],第一段中所有元素都比nums[mid](这就是那个基准数)小,第三段中所有元素都大于等于基准数。
递归求解:递归调用快排分别对nums[mid]的左右两段分别排序
合并:当每一小段就地排序都排好序后,整个数组就已经排完了
实现代码
void Print(int* nums, int n)
{
for (int i = 0; i < n; i++)
{
printf("%-5d", nums[i]);
}
printf("\n");
}
int Partition(int* nums,int left,int right)
{
int l = left, r = right;
int tmp = nums[l];
while (l < r)
{//确保l,r不错位每个都要判断l<r
while (l<r && nums[r]>tmp)r--;//先找右边比tmp小的值
if (l < r)nums[l] = nums[r];
while (l< r && nums[l]<= tmp)l++;//在找左边比tmp大的值
if (l< r)nums[r] = nums[l];
}
//l,r指针重合
nums[l] = tmp;
return l;
}
void QuickSort(int* nums, int left ,int right)
{
if(left<right)
{
int mid = Partition(nums, left, right);//划分函数
QuickSort(nums, left, mid - 1);
QuickSort(nums, mid + 1, right);
}
}划分时一定要先从右边开始扫描
时间复杂度
一般在问题规模为n时时间复杂度T(n)= Ο(nlogn)。最坏情况,数据从小到大或从大到小有序时T(n) = Ο(n^2) 。
快排的优化
随机选择策略
在快排的每一步当数组还没有被划分时,在数组中随机选出一个元素作为划分基准,划分基准随机则划分是比较对称的。用stand()指定一个随机起始点,然后将随机数模数组长度。因为这个right - left是相对位置的长度,但使用的下标rapos必须为绝对位置的下标,所以需要+left。
将随机选择的基准值交换到第一个位置,然后再使用划分函数。
int RandomPartition(int* nums, int left, int right)
{
srand(time(nullptr));//随机种子
int rapos = rand() % (right - left + 1)+left;//取模
std::swap(nums[left], nums[rapos]);//交换两个下标的值
return Partition(nums, left, right);
}三位取中法
left ,right ,mid三个位置的元素取中间大小的元素作为基准值。如nums[left] = 12,nums[mid]=8,nums[right]=10;则取nums[right]作为基准。
struct Index
{
int val;
int index;
};
int MedionThree(int* nums, int left, int right)
{
int mid = left + (right - left >> 1);
struct Index idx[] = { {nums[left],left},{nums[mid],mid},{nums[right],right} };
for (int i = 0; i < 3; i++)//找到中间大的数放到数组头做基准值
{
switch(i)
{
case 0:
if ((idx[i].val - idx[1].val) * (idx[i].val - idx[2].val) < 0)
{ std::swap(nums[idx[i].index], nums[left]); }
break;
case 1:
if ((idx[i].val - idx[0].val) * (idx[i].val - idx[2].val) < 0)
{
std::swap(nums[idx[i].index], nums[left]);
}
break;
case 2:
if ((idx[i].val - idx[0].val) * (idx[i].val - idx[1].val) < 0)
{
std::swap(nums[idx[i].index], nums[left]);
}
break;
}
}
return Partition(nums, left, right);
}非递归的快排
算法递归的部分在于划分后将不同子串输入进去继续划分。非递归时可以将子串的边界装在队列中,之后依次取出作为划分的左右边界。当队列为空,即划分完所有的以后结束。
void QuickSort(int* nums, int left, int right)
{
queue<int> qu;//队列
qu.push(left);
qu.push(right);
while(!qu.empty())
{
int sleft = qu.front(); qu.pop();//取队头,出left
int sright = qu.front(); qu.pop();
int mid = Partition(nums, sleft, sright);
if (sleft < mid - 1)//左边有一个以上元素,仍需划分
{
qu.push(sleft);
qu.push(mid - 1);
}
if (mid + 1 < right)
{
qu.push(mid + 1);
qu.push(sright);
}
}
}