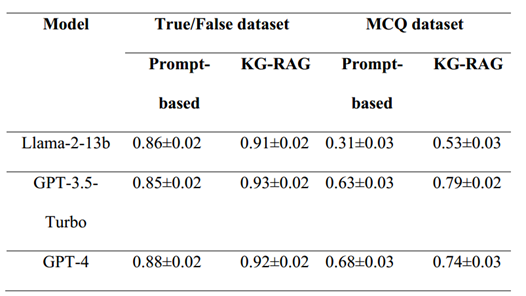
0-1背包问题

问题：背包的容量为9，有重量分别为[2, 4, 6, 9]的四个物品，价值分别为[3, 4, 5, 6]，求背包能装的物品的最大价值是多少，每种物品的数量最多为1

二维数组

w = [2, 4, 6, 9]  # 重量
v = [3, 4, 5, 6]  # 价值
c = 9  # 最大容量
n = len(w)  # 物品数量
w.insert(0, 0)
v.insert(0, 0)
dp = [[0] * (c + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
    for j in range(1, c + 1): # 正向
        if j >= w[i]:
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])
        else:
            dp[i][j] = dp[i - 1][j]

for rows in dp:
    print(rows)
print('最大value：', dp[n][c])

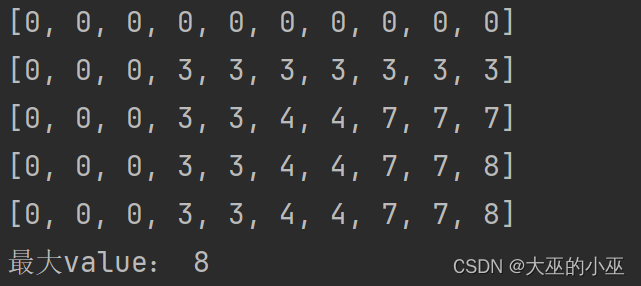
一维数组

w = [2, 4, 6, 9]  # 重量
v = [3, 4, 5, 6]  # 价值
c = 9  # 最大容量

n = len(w)  # 物品数量
w.insert(0, 0)
v.insert(0, 0)
dp = [0] * (c + 1)
for i in range(1, n + 1):
    for j in range(c, 0, -1): # 逆向
        if j >= w[i]:
            dp[j] = max(dp[j], dp[j - w[i]] + v[i])
    print(dp)
print('最大value：', dp[c])

完全背包问题

问题：背包的容量为9，有重量分别为[2, 4, 6, 9]的四个物品，价值分别为[3, 4, 5, 6]，求背包能装的物品的最大价值是多少，每种物品的数量最多不限

二维数组

w = [2, 4, 6, 9]  # 重量
v = [3, 4, 5, 6]  # 价值
c = 9  # 最大容量

n = len(w)
w.insert(0, 0)
v.insert(0, 0)

dp = [[0] * (c + 1) for _ in range(n + 1)]

for i in range(1, n + 1):
    for j in range(1, c + 1): # 正向
        if j >= w[i]:
            dp[i][j] = max(dp[i - 1][j], dp[i][j - w[i]] + v[i])
        else:
            dp[i][j] = dp[i - 1][j]
for values in dp:
    print(values)
print('最大value：', dp[n][c])

一维数组

w = [2, 4, 6, 9]  # 重量
v = [3, 4, 5, 6]  # 价值
c = 9  # 最大容量

n = len(w)

w.insert(0, 0)
v.insert(0, 0)

dp = [0] * (c + 1)

for i in range(1, n + 1):
    for j in range(0, c + 1): # 正向
        if j >= w[i]:
            dp[j] = max(dp[j], dp[j - w[i]] + v[i])
    print(dp)
print('最大value：', dp[c])

多重背包问题

问题：背包的容量为10，有重量分别为[2, 4, 6, 9]的四个物品，价值分别为[3, 4, 5, 6]，求背包能装的物品的最大价值是多少，每种物品的数量最多分别为[2, 1, 2, 1]

一维数组

w = [2, 4, 6, 9]  # 重量
v = [3, 4, 5, 6]
counts = [2, 1, 2, 1]  # 数量
c = 10  # 最大容量
n = len(w)

w.insert(0, 0)
v.insert(0, 0)
counts.insert(0, 0)

dp = [0] * (c + 1)

for i in range(1, n + 1):
    for j in range(c, 0, -1): # 逆向
        for k in range(1, counts[i] + 1):
            if j >= k * w[i]:
                dp[j] = max(dp[j], dp[j - k * w[i]] + v[i])
    print(dp)
print('最大value：', dp[c])