双指针介绍

双指针算法是一种常用的算法技巧，它通常用于在数组或字符串中进行快速查找、匹配、排序或移动操作。 pointer
双指针并非真的用指针实现，一般用两个变量来表示下标（在后面都用指针来表示）。
双指针算法使用两个指针在数据结构上进行迭代，并根据问题的要求移动这些指针。
双指针往往也和单调性、排序联系在一起，在数组的区间问题上，暴力法的时间复杂度往往是O（n^2）的，但双指针利用“单调性”可以优化到O（n）。
常见的双指针模型有： 1）对撞指针 2）快慢指针

对撞指针

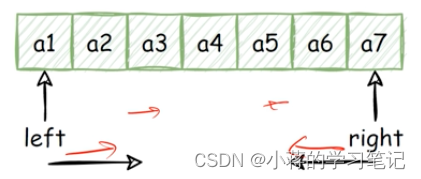
指的是两个指针left、right（简写为1，r）分别指向序列第一个元素和最后一个元素。然后1指针不断递增，r不断递减，直到两个指针的值相撞或错开（即1>=r），或者满足其他
要求的特殊条件为止。 对撞指针一般用来解决有序数组或者字符串问题（常见于区间问题）：
查找有序数组中满足某些约束条件的一组元素问题:比如二分查找、数字之和等问题。字符串反转问题：反转字符串、回文数、颠倒二进制等问题。

1. 使用两个指针left，right。left指向序列第一个元素，即：left=1，right指向序列最后 一个元素，即：right= n。
2. 在循环体中将左右指针相向移动，当满足一定条件时，将左指针右移，left++。当满足另 外一定条件时，将右指针左移，right-。
3. 直到两指针相撞（即left==right），或者满足其他要求的特殊条件时，跳出循环体。
   

回文判定

#include<bits/stdc++.h>

using namespace std;

string s;

int main( ){
    cin>>s;
    unsigned long i = 0,j = s.length()-1;
    bool flag = true;
    while(i<j&&flag){
        if(s[i]!=s[j])flag = false;
        i++,j--;
    }
    cout<<(flag==true?"Y":"N")<<endl;
    return 0;
}

快慢指针

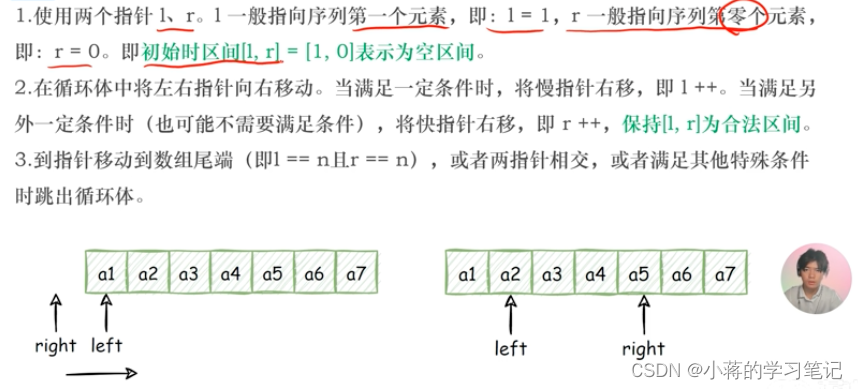
快慢指针一般比对撞指针更难想，也更难写 指的是两个指针从同一侧开始遍历序列，且移动的步长一个快一个慢。
移动快的指针被称为快指针，移动慢的指针被称为慢指针。
为了方便理解，我们成快指针为r，慢指针为l，这样慢指针和快指针构成区间［l，r］。两个指针以不同速度、不同策略移动，直到快指针移动到数组尾端，或者两指针相交，或老
满足其他特殊条件时为止。

lanqiao OJ 1372 美丽的区间

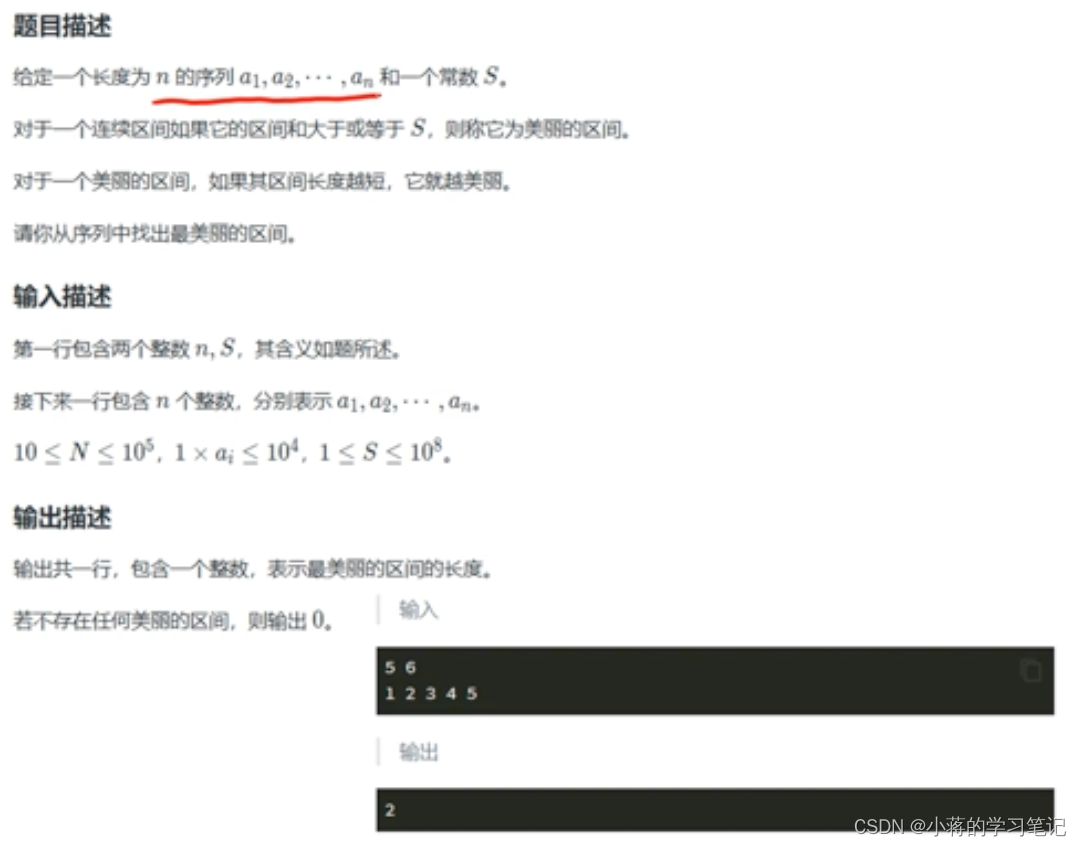
#include<bits/stdc++.h>

using namespace std;
typedef long long ll;
int n,S;

int main( ){
    cin>>n>>S;
    vector<int> arr(n);
    
    for(int i=1;i<=n;i++)cin>>arr[i];
    int res = n+1;
    for(int i=1,j=0,sum=0;i<=n;i++){
        while(i>j||(j+1<=n&&sum<S))sum+=arr[++j];
        if(sum>=S)res = min(res,j-i+1);
        sum-=arr[i];
    }
    cout<<(res>n?0:res)<<'\n';
    return 0;
}

lanqiao OJ 1621 挑选子串

#include<bits/stdc++.h>

using namespace std;

int n,m,k;

int main( ){
    cin>>n>>m>>k;
    vector<int>a(n);
    for(int i=1;i<=n;i++)cin>>a[i];
    long long ans = 0;
    for(int i=1,j=0,cnt=0;i<=n;i++){
        while(i>j||(j+1<=n&&cnt<k)){
            if(a[++j]>=m){
                cnt++;
            }
        }
        if(cnt>=k)ans+=n-j+1;
        if(a[i]>=m)cnt--;
    }
    cout<<ans<<endl;
    return 0;
}

蓝桥杯2023年第十四届省赛真题-子串简写

解法一：双指针

#include<bits/stdc++.h>

using namespace std;

string s;
int k,cnt;
char c1,c2;
long long ans;

int main( ){
    cin>>k>>s>>c1>>c2;
    unsigned long n = s.length();
    for(int i=0,j=k-1;j<n;i++,j++){
        if(s[i]==c1)cnt++;
        if(s[j]==c2)ans+=cnt;
    }
    cout<<ans<<endl;
    return 0;
}

解法二：前缀和

#include<bits/stdc++.h>

using namespace std;

string s;
int k,cnt,t;
char c1,c2;
long long ans;

int main( ){
    cin>>k>>s>>c1>>c2;
    unsigned long n = s.length();
    vector<int>sum(n);
    
    for(int i=0;i<n;i++){
        if(s[i]==c1)t++;
        sum[i]=t;
        if(s[i]==c2&&i>=k-1)ans+=sum[i-k+1];
    }
    cout<<ans<<endl;
    return 0;
}

解法三：二分

#include<bits/stdc++.h>

using namespace std;

string s;
int k,cnt,t;
char c1,c2;
long long ans;

int main( ){
    cin>>k>>s>>c1>>c2;
    unsigned long n = s.length();
    vector<int> st,ed;
    for(int i=0;i<n;i++){
        if(s[i]==c1)st.push_back(i);
        if(s[i]==c2)ed.push_back(i);
    }
    for(int i=0;i<st.size();i++){
        int x = st[i];
        int X = x+k-1;
        int l=0,r=ed.size()-1;
        while(l<r){
            int mid = (l+r)>>1;
            if(ed[mid]>=X)r=mid;
            else l=mid+1;
        }
        if(ed[l]>=X)ans+=ed.size()-l;
    }
    cout<<ans<<endl;
    return 0;
}