1.概述

前缀和算法分为一维和二维，一维前缀和可以快速求序列中某一段的和，而二维前缀和可以快速求一个矩阵中某个子矩阵的和。

2.代码实现

2.1.一维前缀和

（1）实现代码如下：

class NumArray {
    //前缀和数组，preSum[i] 表示 nums[0...i - 1] 的累加和
    private int[] preSum;
    
    //输入数组 nums，构造前缀和
    public NumArray(int[] nums) {
        // preSum[0] = 0，便于计算累加和
        preSum = new int[nums.length + 1];
        for (int i = 1; i < preSum.length; i++) {
            preSum[i] = preSum[i - 1] + nums[i - 1];
        }
    }
    
    //查询闭区间 nums[left, right] 的累加和
    public int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
}

（2）下面对代码中一些细节进行说明：

前缀和数组 preSum 的长度之所以设置为 nums.length + 1 而非 nums.length，其原因在于方便计算累加和；
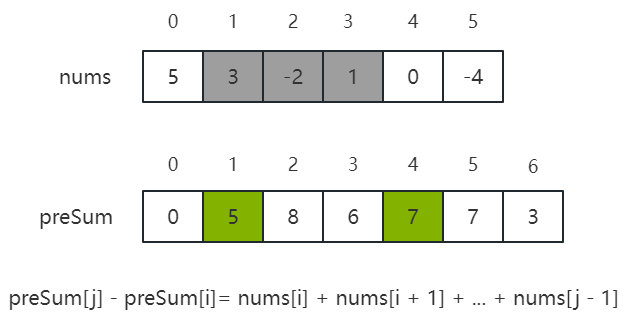
preSum[i] 表示 nums[0…i - 1] 的累加和，那么推导出 preSum[i] = preSum[i - 1] + nums[i - 1]，如下图所示：
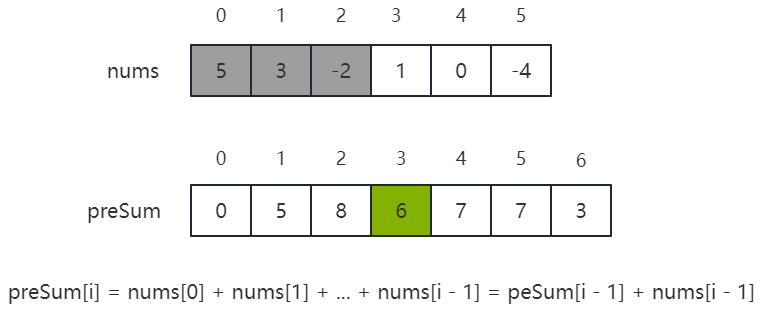
在有了前缀和数组 preSum 后，如果想要查询区间 nums[i…j] 的累加和，那么计算 preSum[j + 1] - preSum[i] 的值即可，如下图所示：

2.2.二维前缀和

（1）实现代码如下：

class NumMatrix {
    // preSum[i][j] 表示矩阵 matrix 中左上角坐标为 [0, 0]、右下角坐标为 [i - 1, j - 1] 的子矩阵的元素和
    private int[][] preSum;
    
    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        if (m == 0 || n == 0) {
            return;
        }
        //构造前缀和矩阵
        preSum = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // 计算每个左上角坐标为 [0, 0]、右下角坐标为 [i - 1, j - 1] 的子矩阵的元素和
                preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] + matrix[i - 1][j - 1] - preSum[i - 1][j - 1];
            }
        }
    }
    
    //计算矩阵 matrix 中左上角坐标为 [x1, y1]、右下角坐标为 [x2, y2] 的子矩阵的元素和
    public int sumRegion(int x1, int y1, int x2, int y2) {
        return preSum[x2 + 1][y2 + 1] - preSum[x1][y2 + 1] - preSum[x2 + 1][y1] + preSum[x1][y1];
    }
}

（2）下面对代码中一些细节进行说明：

设下图中绿色子矩阵的左上角坐标为 [x1, y1]、右下角坐标为 [x2, y2]，那么它可以由下图中右边的 4 个子矩阵通过加减组合得到：

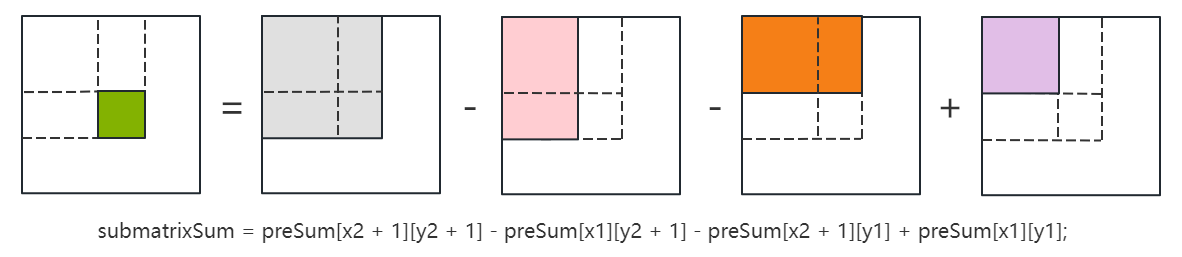
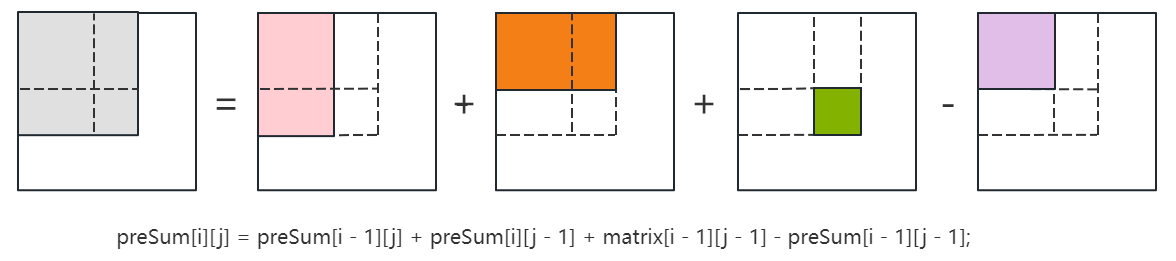
在这里插入图片描述

在初始化前缀和矩阵 preSum 时，需要计算每个左上角坐标为 [0, 0]、右下角坐标为 [i - 1, j - 1] 的子矩阵的元素和，此时只需要将上面的等式稍作变换即可，如下图所示。不过需要注意的是绿色子矩阵的边长为 1，即对应矩阵 matrix 中的一个元素。

在这里插入图片描述

3.应用

（1）前缀和算法的使用场景：原数组/矩阵在不会被修改的前提下，频繁地对其某个区间/子矩阵的累加和进行查询操作。如果只需要查询一次，那么使用前缀和算法的意义不大；而如果频繁地进行查询操作，那么前缀和算法的优势便体现出来了：
① 在构建前缀和数组/矩阵时，其时间复杂度为 O(n) / O(mn)，而在频繁地进行查询操作时，其时间复杂度仅为 O(1)；
② 如果直接进行累加操作，则需要进行多次时间复杂度为 O(n) / O(mn) 的操作（注：此处的 n 和 mn 取决于要查询的区间 / 子矩阵大小）。

（2）下面以 LeetCode 中的304.二维区域和检索 - 矩阵不可变这题为例：

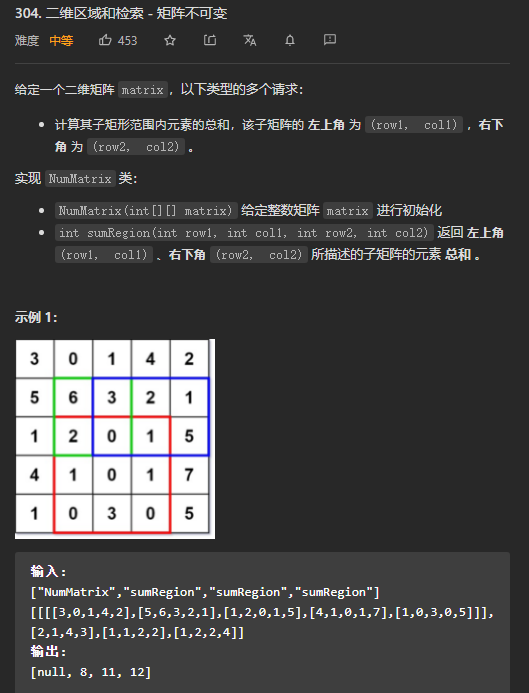
在这里插入图片描述

本题就是典型地要频繁地对其矩阵 matrix 中的子矩阵的累加和进行查询操作，其对应的实现代码如下：

class NumMatrix {
    /*
        前缀和矩阵preSum记录矩阵matrix[0,0,i,j]的元素和
        preSum[i][j]=左上角(0,0)、右下角(i-1,j-1)所描述的子矩阵的元素总和
    */
    private int[][] preSum;
    
    public NumMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        //构造前缀和矩阵
        preSum = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] + matrix[i - 1][j - 1] - preSum[i - 1][j - 1];
            }
        }
    }
    
    //计算左上角(row1, col1)、右下角(row2, col2)所描述的子矩阵的元素总和
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return preSum[row2 + 1][col2 + 1] - preSum[row1][col2 + 1] - preSum[row2 + 1][col1] + preSum[row1][col1];
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */