[蓝桥杯 2018 省 B] 螺旋折线

题目描述

如图所示的螺旋折线经过平面上所有整点恰好一次。

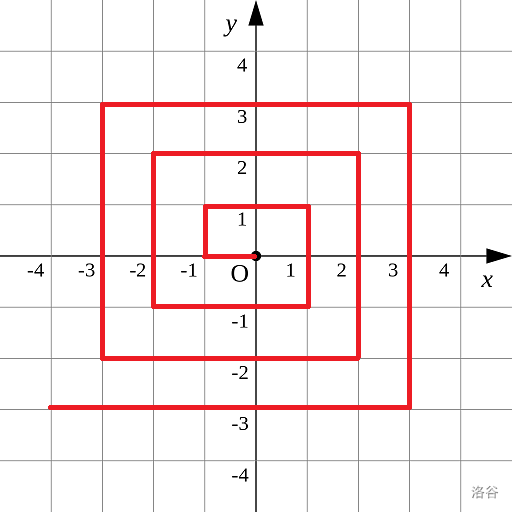
对于整点 $(X,Y)$，我们定义它到原点的距离 $\text{dis}(X,Y)$ 是从原点到 $(X,Y)$ 的螺旋折线段的长度。

例如 $\text{dis}(0,1)=3$，$\text{dis}(-2,-1)=9$。

给出整点坐标 $(X,Y)$，你能计算出 $\text{dis}(X,Y)$ 吗？

输入格式

$X$ 和 $Y$。

输出格式

输出 $\text{dis}(X,Y)$

样例 #1

样例输入 #1

0 1

样例输出 #1

3

提示

对于 $40\%$的数据，$-1000\le X,Y\le 1000$。

对于 $70\%$ 的数据，$-10^5\le X,Y\le 10^5$。

对于 $100\%$ 的数据，$-10^9\le X,Y\le 10^9$。

---

思路

暴力模拟会超时，不妨想想其他办法。

函数d(int t)计算从原点到点(-t, t)的螺旋折线距离，使用等差数列求和公式2t * (2t + 1) * 2 / 2。

函数dis(int x, int y)是主要的计算函数，根据输入的坐标点(x, y)，计算出螺旋折线距离。

观察到有三条分界线：$y=x$ 、$y=-x$、$y=x+1$ 将图形分为四个部分。可以对每个区域分类讨论，通过从原点到点(-t, t)的螺旋折线距离，换算出从原点到任意点(x, y)的螺旋折线距离。

• 当点位于左侧区域，并且满足条件$x\ge 0$，$-x\le y$，$y<x$时，此时的螺旋折线距离可以通过公式$d(t)+3\ast t-y$计算，其中$t=x$。

• 当点位于上侧区域，并且满足条件$y>0$，$-y<x$，$x\le y$时，此时的螺旋折线距离可以通过公式$d(t)+t+x$计算，其中$t=y$。

• 当点位于右侧区域，并且满足条件$x<0$，$x+1<y$，$y\le -x$时，此时的螺旋折线距离可以通过公式$d(t)-t+y$计算，其中$t=-x$。

• 当点位于下侧区域，此时的螺旋折线距离可以通过公式$d(t)-3\ast t-x+1$计算，其中$t=-y+1$。

在main函数中，使用cin从输入中读取坐标点(x, y)，然后调用dis(int x, int y)计算螺旋折线距离，并使用cout输出结果。

注意

对于 $100\%$ 的数据，$-10^9\le X,Y\le 10^9$。dis 可能会超出 int 的范围。需要开 long long，否则无法通过部分测试点。

---

AC代码

#include <algorithm>
#include <iostream>
#define mp make_pair
#define AUTHOR "HEX9CF"
using namespace std;
using ll = long long;

const int N = 1e6 + 7;
const int INF = 0x3f3f3f3f;
const ll MOD = 1e9 + 7;

// 从原点到(-t, t)
ll d(int t) {
	// 2t * (2t + 1) * 2 / 2
	return (1ll * 2 * t * (2 * t - 1));
}

ll dis(int x, int y) {
	if (x >= 0 && -x <= y && y < x) {
		// 右
		int t = x;
		// d + 2t + (t - y)
		return (1ll * d(t) + 3 * t - y);
	} else if (y > 0 && -y < x && x <= y) {
		// 上
		int t = y;
		// d + (t - x)
		return (1ll * d(t) + t + x);
	} else if (x < 0 && x + 1 < y && y <= -x) {
		// 左
		int t = -x;
		// d - (t - y)
		return (1ll * d(t) - t + y);
	} else {
		// 下
		int t = -y + 1;
		// d - (2t - 1) - (x + t)
		return (1ll * d(t) - 3 * t - x + 1);
	}
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	int x, y;
	cin >> x >> y;
	cout << dis(x, y) << "\n";

	return 0;
}