目录

51.N皇后 

37.解数独

---

51.N皇后 

51. N 皇后

困难

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

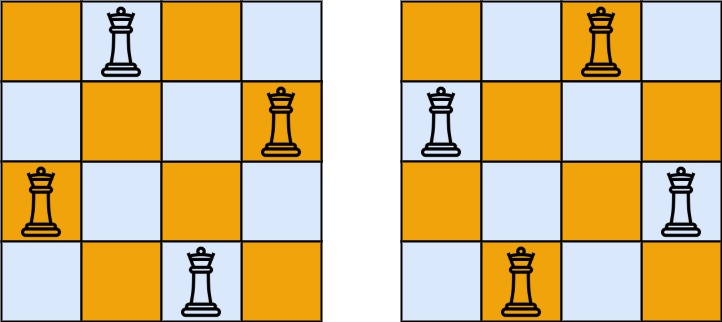
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

• 1 <= n <= 9

// 类定义  
class Solution {  
    // 结果列表，用于存储所有有效的N皇后解  
    List<List<String>> res = new ArrayList<>();
    // 用于记录当前棋盘上的皇后位置  
    int[] board;
    // 布尔数组，用于标记已经占用的列  
    boolean[] usedCol;  
    // 布尔数组，用于标记已经占用的45度斜线  
    boolean[] usedDiag45;  
    // 布尔数组，用于标记已经占用的135度斜线  
    boolean[] usedDiag135;  
  
    // 主方法，接收棋盘的大小n，返回所有有效的N皇后解  
    public List<List<String>> solveNQueens(int n) {  
        // 初始化列方向的布尔数组  
        usedCol = new boolean[n];  
        // 初始化45度斜线方向的布尔数组，长度为2n-1，因为从第一行到最后一行，斜线数量逐渐增加  
        usedDiag45 = new boolean[2 * n - 1];  
        // 初始化135度斜线方向的布尔数组，同样长度为2n-1  
        usedDiag135 = new boolean[2 * n - 1];  
  
        // 用于记录当前棋盘上的皇后位置，board[i]表示第i行皇后的列位置  
        board = new int[n];  
        // 开始回溯，从第0行开始尝试放置皇后  
        backTracking(n, 0);  
        // 返回结果  
        return res;  
    }  
  
    // 回溯方法，接收当前棋盘状态、棋盘大小n和当前尝试放置皇后的行号row  
    private void backTracking(int n, int row) {  
        // 如果已经放置了n个皇后，说明找到了一个有效的解，将其添加到结果列表中  
        if (row == n) {  
            List<String> temp = new ArrayList<>();  
            // 将当前棋盘状态转换为字符串列表，并添加到temp中  
            for (int i : board) {  
                char[] str = new char[n];  
                Arrays.fill(str, '.'); // 初始化字符串为'.'，表示没有皇后  
                str[i] = 'Q'; // 在对应位置放置皇后  
                temp.add(new String(str)); // 将字符串添加到temp中  
            }  
            res.add(temp); // 将temp添加到结果列表中  
            return;  
        }  
  
        // 尝试在当前行的每一列放置皇后  
        for (int col = 0; col < n; col++) {  
            // 如果当前列、45度斜线或135度斜线已经被占用，则跳过当前列  
            if (usedCol[col] || usedDiag45[row + col] || usedDiag135[row - col + n - 1]) {  
                continue;  
            }  
  
            // 在当前列放置皇后，并记录位置  
            board[row] = col;  
            // 标记当前列、45度斜线和135度斜线为已占用  
            usedCol[col] = true;  
            usedDiag45[row + col] = true;  
            usedDiag135[row - col + n - 1] = true;  
  
            // 递归尝试放置下一个皇后  
            backTracking(n, row + 1);  
  
            // 回溯，撤销之前的操作
            board[row] = 0;  
            usedCol[col] = false;  
            usedDiag45[row + col] = false;  
            usedDiag135[row - col + n - 1] = false;  
        }  
    }  
}

37.解数独

37. 解数独

困难

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

数独部分空格内已填入了数字，空白格用 '.' 表示。

示例 1：

输入：board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
输出：[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
解释：输入的数独如上图所示，唯一有效的解决方案如下所示：

提示：

• board.length == 9
• board[i].length == 9
• board[i][j] 是一位数字或者 '.'
• 题目数据 保证 输入数独仅有一个解

class Solution {  
    public void solveSudoku(char[][] board) {  
        // 调用辅助方法来解决数独问题  
        solveSudokuHelper(board);  
    }  
  
    private boolean solveSudokuHelper(char[][] board){  
        // 遍历棋盘的每一行  
        for (int i = 0; i < 9; i++){  
            // 遍历棋盘的每一列  
            for (int j = 0; j < 9; j++){  
                // 如果当前位置已经有数字，则跳过该位置  
                if (board[i][j] != '.'){  
                    continue;  
                }  
                // 尝试在(i, j)位置放置1到9的每一个数字  
                for (char k = '1'; k <= '9'; k++){  
                    // 检查(i, j)位置放置k是否合法  
                    if (isValidSudoku(i, j, k, board)){  
                        // 如果合法，则放置数字k  
                        board[i][j] = k;  
                        // 递归地尝试填充下一个位置  
                        if (solveSudokuHelper(board)){  
                            // 如果递归调用返回true，说明找到了解，直接返回true  
                            return true;  
                        }  
                        // 如果递归调用返回false，则回溯，撤销放置的数字k  
                        board[i][j] = '.';  
                    }  
                }  
                // 如果(i, j)位置放置1到9的数字都不合法，则返回false  
                // 这表示当前路径无解，需要回溯到上一层尝试其他可能  
                return false;  
            }  
        }  
        // 如果遍历完所有位置都没有返回false，说明已经成功填充了所有位置，返回true  
        return true;  
    }  
  
    /**  
     * 验证在棋盘的指定位置放置某个数字是否合法  
     * @param row 行号  
     * @param col 列号  
     * @param val 要放置的数字  
     * @param board 数独棋盘  
     * @return 如果合法返回true，否则返回false  
     */  
    private boolean isValidSudoku(int row, int col, char val, char[][] board){  
        // 检查同一行是否重复  
        for (int i = 0; i < 9; i++){  
            if (board[row][i] == val){  
                return false;  
            }  
        }  
        // 检查同一列是否重复  
        for (int j = 0; j < 9; j++){  
            if (board[j][col] == val){  
                return false;  
            }  
        }  
        // 检查3x3的小方格内是否重复  
        int startRow = (row / 3) * 3; // 小方格起始行  
        int startCol = (col / 3) * 3; // 小方格起始列  
        for (int i = startRow; i < startRow + 3; i++){  
            for (int j = startCol; j < startCol + 3; j++){  
                if (board[i][j] == val){  
                    return false;  
                }  
            }  
        }  
        // 如果以上检查都没有重复，则返回true  
        return true;  
    }  
}