上次笔者写了一篇大概有7个题的链表相关的题目+解析,感觉还不错,感兴趣的各位老铁,可以点一下链接进行欣赏:做几个与链表相关的题吧!https://blog.csdn.net/weixin_64308540/article/details/128550685?spm=1001.2014.3001.5502那么,接下来就该进入:环形链表部分了!!
141. 环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:

输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
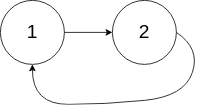
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:false
解释:链表中没有环。
提示:
链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个 有效索引 。
进阶:你能用 O(1)(即,常量)内存解决此问题吗?
上述是力扣中的题目!如果你已经看完了题目,那么,就该跟着笔者进入正文解析了!!
根据链表的基础知识,我们可以得出:如果一个链表是环形链表,那么最后一个节点一定存储了前面某个节点的地址!!

思路:快慢指针:
快慢指针,即慢指针一次走一步,快指针一次走两步,两个指针从链表的起始位置(头节点)开始进行,如果链表带环,则快指针与慢指针一定会在环中相遇!!否则,快指针一定会率先走到链表的尾部,比如,陪女朋友到操场跑步减肥!!
扩展问题:
为什么快指针一次走两步,慢指针一次走一步可以??
假设链表带环,两个指针最后都会进入环,快指针先进入环,慢指针后进入环,当慢指针刚进入环时候,可能就与快指针相遇了,最差的情况下,两个指针的距离就是环的长度!此时两个指针每移动一次,之间的距离就缩小一步,,不会出现每次刚好是套圈的情况,因此,在慢指针走一圈之前,快指针肯定可以追上慢指针的!即相遇!
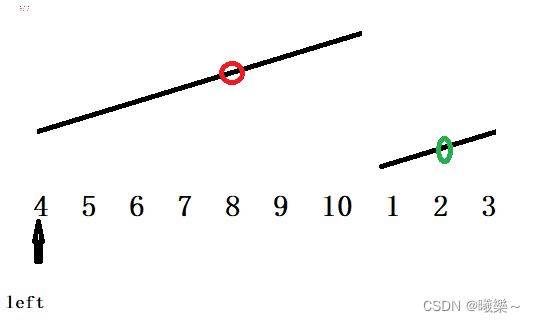
2.快指针一次走3步,走4步,...n步行吗? 假设有环的情况下:快指针每次走3步,慢指针每次走1步,此时快指针肯定先进环,慢指针后来才进环,假设慢指针进环的时候,快慢指针的相对位置如图所示:

此时按照上述的假设:快指针每次走3步,慢指针每次走1步,来绕环移动,是永远不会相遇的!!此时进行了套圈!!

因此,只有快指针走2步,慢指针走1步才可以,换的是最小长度是1,即使套圈了,两个也能在相同位置!!
此时我们可以看出,环的问题,可以大致理解为:追及相遇的问题!!
那么,有了这些想法,我们还应该判断没环的情况下的问题:

经过上述的分析,我们可以看出当没环条件下的结束条件!
因此,我们有着下述的简单代码:写法1:
public boolean hasCycle(ListNode head){
ListNode fast=head;
ListNode slow=head;
while (fast != null && fast.next !=null){ //没环的情况下!
fast=fast.next.next;
slow=slow.next;
if (fast==slow){
return true;
}
}
return false;
}写法2:
public boolean hasCycle2(ListNode head){
ListNode fast=head;
ListNode slow=head;
while (fast != null && fast.next !=null){
fast=fast.next.next;
slow=slow.next;
if (fast==slow){
break;//出while循环(有两种可能)
}
}
if (fast==null ||fast.next==null){//排除不是环的可能
return false;
}
return true;
}经过这个题目,我们可以思考一下,如何进行手动置环??
手动置环问题:遍历一遍链表,找到尾巴节点,其所对应的next本为null,将其改为前面任意节点的地址就可以了(保证有)!!
//手动置环
public void creatLoop(ListNode head){
ListNode cur=head;
while (cur.next !=null){
cur=cur.next;//找尾巴节点
}
cur.next=head.next.next;//保证有该节点!
}142. 环形链表 II
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
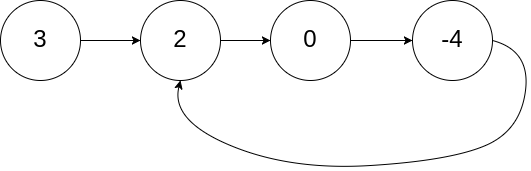
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:

输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
链表中节点的数目范围在范围 [0, 104] 内
-105 <= Node.val <= 105
pos 的值为 -1 或者链表中的一个有效索引
进阶:你是否可以使用 O(1) 空间解决此题?
对于这个题目,显得有点儿难度!!
结论 让一个指针从链表起始位置开始遍历链表,同时让一个指针从判环时相遇点的位置开始绕环运行,两个指针都是每次均走一步,最终肯定会在入口点的位置相遇。 证明
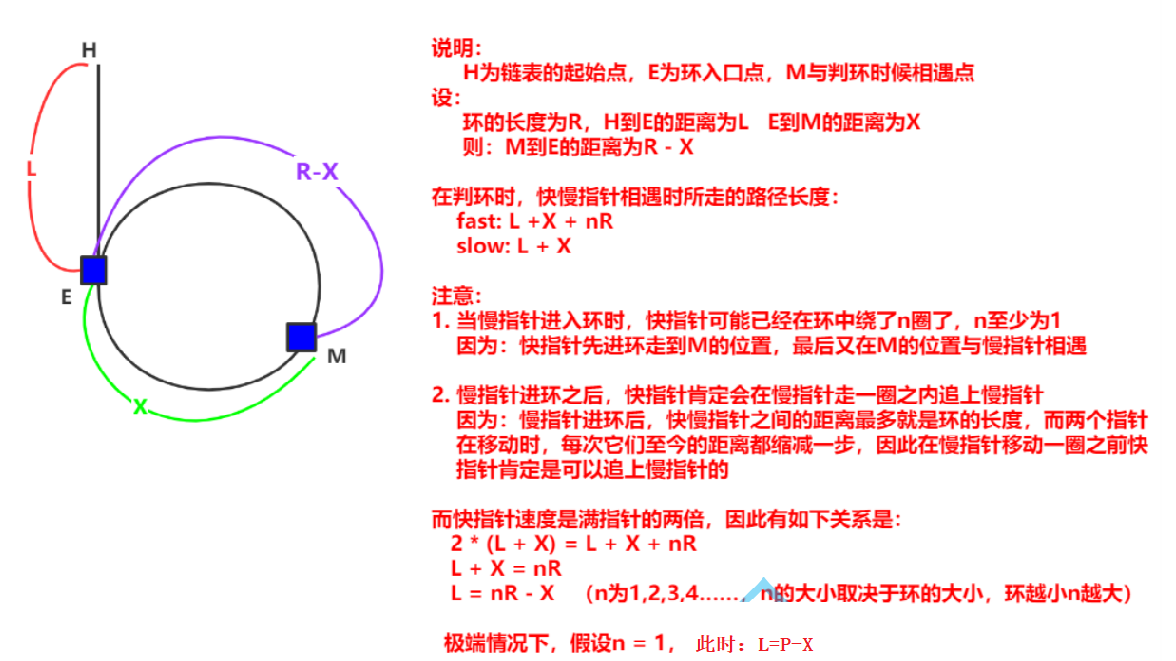
这个是主要的思路,或许你看不懂,没关系,那么请看一下笔者的推论吧!!
我们有着以下的简单思路:

当在最好的情况下:我们有着:fast多走一圈,然后与slow在相遇处相遇,此时,fast走的路程为:X+C(C-Y) 此时,slow走的路程:X+(C-Y),由于fast的速度是slow的二倍,则路程也是2倍,即有着一下结论:2*(X+C-Y)=X+C+(C-Y) 经过计算,我们可以得到;X==Y
当不最好的情况下:fast走了很多圈,才与slow在相遇点相遇,此时说明,环的长度C很小很小!!

此时,fast走的路程为:X+NC(C-Y) 此时,slow走的路程:X+(C-Y),由于fast的速度是slow的二倍,则路程也是2倍,即有着一下结论:2*(X+C-Y)=X+NC+(C-Y) 经过计算,我们可以得到;X==(N-1)*C+Y 因此,当N很大很大的时候,说明环很小很小了,而fast多走的长是从相遇点开始的!!
注意:
当慢指针进入环时候,快指针可能已经在环中绕了N圈了,N至少为1,因为当快指针先到环走到相遇点的位置,慢指针还没有进环!
慢指针进入环以后,快指针肯定会在慢指针走一圈之内追上慢指针,因为:快指针进环之后,快慢指针之间的距离最多就是环的长度,而两个指针在移动的时候,每次他们之间的距离都会缩减1步,因此,慢指针移动一圈之前,快指针一定可以追上慢指针的!!
下面请看笔者的代码吧!!代码起很简单,但是思路很重要!!
//返回循环链表的相交节点
public ListNode detectCycle(ListNode head){
ListNode fast=head;
ListNode slow=head;
//先判断链表中是否有环??
while (fast != null && fast.next !=null){
fast=fast.next.next;
slow=slow.next;
if (fast==slow){
break;
}
}
if (fast == null || fast.next == null){
return null;
}
//此时fast与slow已经在相遇点相遇了!
slow=head;//将fast或者slow任意一个拉回头节点head
while (fast !=slow){
fast=fast.next;
slow=slow.next;
}//当fast与slow再次相遇的时候,即为入口点
return fast;
}对于这个代码,想必各位老铁都能看懂吧!!
由于在码字的过程中,出现了些许差错,导致有点错别字!!勿怪!勿怪!