目录

二分查找算法思想：

循环

递归

有多个与key相等数据的查询，找最左边与关键字相等的那个

找第一个大于key的元素的下标

有序循环数组的二分查找

---

二分查找算法思想：

二分查找也叫折半查找，查找效率较高。但是查找的线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

       线性表元素升序排列，将线性表中间位置的关键字与查找关键字比较，如果两者相等，则查找成功，否则将线性表一分为二。分治策略

如果中间位置的值大于查找关键字，则在左子表继续查找，否则查找右子表。

重复以上过程直到查找成功，返回位置信息。若子表为空了仍未找到返回-1，查找失败。

二分查找的时间复杂度是O(log(n))，最坏情况下的时间复杂度是O(n)。

---

循环

int binary_search(const int* nums, int n, int key)
{
	int left = 0;
	int right = n - 1;
	int mid = 0;
	int pos = -1;
	while (left <= right)//left和right是数据的规模，==时还有一个数据在里面，所以必须有=而非left<right
	{
		mid = (left + right) / 2;
		//也可以写成  mid = (right-left)/2+left，+left因为他是一个绝对规模，不能相对相减
		if (nums[mid] > key)
			right = mid - 1;
		else if (nums[mid] < key)
			left = mid + 1;
		else
		{
			pos = mid;
			break;
		}
	}
	return pos;
}

递归

        分治策略处理一个区域时，不能只用一个参数控制

int Find(const int* nums, int left, int right, int key)
{
	if (left <= right)
	{
		int mid = left + ((right - left) >> 1);
		if (nums[mid] > key)
			return Find(nums, left, mid - 1, key);
		else if (nums[mid] < key)
			return Find(nums, mid + 1, right, key);
		else
			return mid;
	}
	return -1;
}
int binarySearch(int* nums, int n, int key)
{
	assert(n > 0);
	int left = 0;
	int right = n - 1;
	return Find(nums, left, right, key);
}

---

有多个与key相等数据的查询，找最左边与关键字相等的那个

算法思想：先用二分查找找到一个与key相同的元素，然后顺序查看其左边的元素是否也与key相同，直到找到最左边的（数组查完/左边元素不等于key）。

算法改进：找到与key相同的元素后查看其左边第一个（不越界的情况下）是否也相同，如果不相同则没有多个，直接返回。如果相同则继续用二分查找找左边子序列与key相同的。

这样是为了避免有如：在序列3 3 3 3 3 3 3 3中查找3，完全没有了二分的优势。

int binary_search(const int* nums, int n, int key)
{
	int left = 0;
	int right = n - 1;
	int mid = 0;
	int pos = -1;
	while (left <= right)
	{
		mid = left + (left + right >> 1);
		if (nums[mid] > key)
			right = mid - 1;
		else if (nums[mid] < key)
			left = mid + 1;
		//else//二分查询到之后线性查询，一个挨着一个找
		//{
		//	while (mid>left && nums[mid-1] == key )//这个调节不能写反，否则越界
		//	{
		//		--mid;
		//	}
		//	pos = mid;
		//	break;
		//}
		//改进
		else
		{
			if (mid == left || nums[mid - 1] != key) return mid;//已经是最左边了
			else
			{
				right = mid - 1;
				continue;
			}
		}
	}
	return pos;
}

---

找第一个大于key的元素的下标

                mid<key，则不用在left-mid区间进行查找。

                mid==key时，如果下一个元素不等于key，则下一个为所找元素；

                                        如果下一个也等于key，则在右子序列继续二分查找。

                mid>key,则与上一题同理。

找第一个小于反之。

int binary_search(const int* nums, int n, int key)
{
	int left = 0;
	int right = n - 1;
	int mid = 0;
	int pos = -1;
	while (left <= right)
	{
		mid = left + (right-left >> 1);
		if (nums[mid] >= key)
		{
			if (nums[mid] == key)
			{
				if (nums[mid + 1] == key)
					left = mid + 1;
				else
					return mid + 1;
			}
			else 
			{
				if (nums[mid - 1] > key)
				{
					right = mid - 1;
				}
				else
					return mid;
			}
		}
		else if (nums[mid] < key)
			left = mid + 1;
	}
	return pos;
}
int main()
{
	int arr[10] = {0,1,2,3,4,5,6,6,8,9};
	printf("%d ", binary_search(arr, 10, 5));
	return 0;
}

---

有序循环数组的二分查找

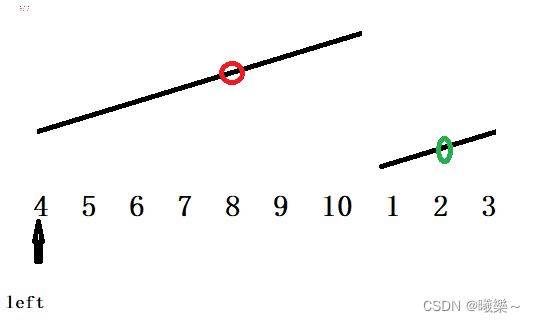
有序循环数组如：4，5，6，7，8，9，10，1，2，3；查询给定的key是否在顺序表中，在哪。
先找到循环的点，再二分查找。

        在一个有序子串中取一值，left一定比它小；在另一子串中取值，left一定比它大。这样产生mid指向任意值，就可以判断循环的断点在mid的左边还是右边了。

 

int binary_search(const int* nums, int n, int key)
{
	int left = 0;
	int right = n - 1;
	int mid=0,bmid=0;
	int pos = -1;
	while (left < right)
	{
		bmid = left + (right - left >> 1);
		if (nums[bmid] == key)
			return bmid;
		else if (nums[left] < nums[bmid])//循环点在bmid右边
		{
			left = bmid;
		}
		else if (nums[left] > nums[bmid])//在bmid左边
		{
			right = bmid;
		}
		else
		{
			bmid++;
			break;
		}
	}
	printf("bmid==%d\n",bmid);
	//找到循环点了
	if (nums[0] <= key)//key应该在左边
	{
		left = 0;
		right = bmid - 1;
	}
	else
	{	
		left = bmid;
		right = n - 1;
	}
	while (left <= right)
	{
		mid = left+(right-left>>1);
		if (nums[mid] > key)
			right = mid - 1;
		else if (nums[mid] < key)
			left = mid + 1;
		else
		{
			pos = mid;
			break;
		}
	}
	return pos;
}
int main()
{
	int arr[10] = { 4,5,6,7,8,9,10,1,2,3};
	printf("%d \n", binary_search(arr, 10, 5));
	return 0;
}