8.4 镜面阵
法向量确定一个镜面
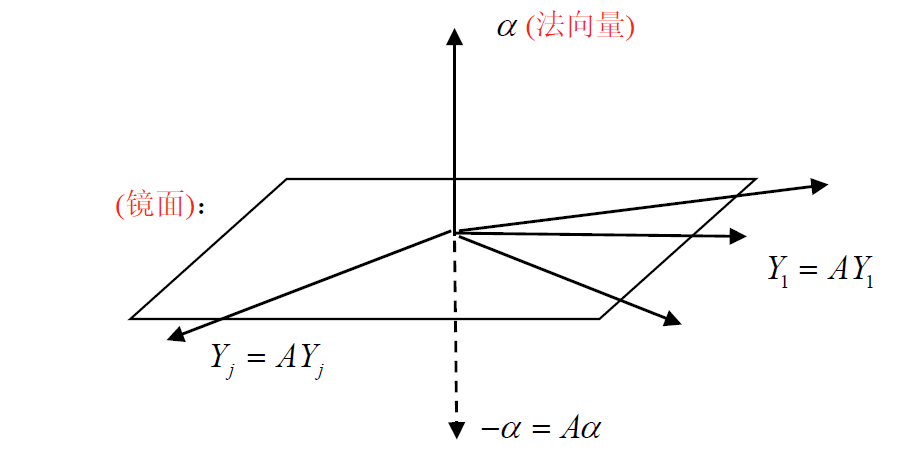
8.4.1 镜面阵的作用
对法向量
- A α = − α A\alpha=-\alpha Aα=−α
- A ( A α ) = A 2 α = α A(A\alpha)=A^2\alpha=\alpha A(Aα)=A2α=α
对镜面上向量
- A Y = Y AY=Y AY=Y
8.4.2 镜面阵表示
A = I n − 2 α α H ∣ α ∣ 2 , 其中 α = ( x 1 x 2 ⋮ x n ) ∈ C n , 且 α ≠ 0 A=I_n-\frac{2\alpha\alpha^H}{\vert \alpha\vert^2},其中 \alpha=\left(\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right)\in C^n,且\alpha\neq 0 A=In−∣α∣22ααH,其中α= x1x2⋮xn ∈Cn,且α=0
令 ϵ = α ∣ α ∣ \epsilon=\frac{\alpha}{\vert \alpha\vert} ϵ=∣α∣α ,镜面阵 A = I − 2 ϵ ϵ H A=I-2\epsilon\epsilon^H A=I−2ϵϵH ,满足 ϵ H ϵ = ∣ ϵ ∣ 2 = 1 \epsilon^H\epsilon=\vert\epsilon\vert^2=1 ϵHϵ=∣ϵ∣2=1
验证:
对于法向量
α
,
A
α
=
(
I
n
−
2
α
α
H
∣
α
∣
2
)
α
=
α
−
2
α
α
H
α
∣
α
∣
2
=
α
−
2
α
∣
α
∣
2
∣
α
∣
2
=
−
α
对于
Y
∈
镜面,有
α
⊥
Y
,
即内积
(
α
,
Y
)
=
(
Y
,
α
)
=
0
,
且
(
Y
,
α
)
=
α
H
Y
=
0
A
Y
=
(
I
n
−
2
α
α
H
∣
α
∣
2
)
Y
=
Y
−
2
α
α
H
Y
∣
α
∣
2
=
Y
\begin{aligned} &对于法向量\alpha,A\alpha=(I_n-\frac{2\alpha\alpha^H}{\vert \alpha\vert^2})\alpha=\alpha-\frac{2\alpha\alpha^H\alpha}{\vert \alpha\vert^2}=\alpha-\frac{2\alpha\vert \alpha\vert^2}{\vert \alpha\vert^2}=-\alpha\\ &对于Y\in 镜面,有\alpha\bot Y,即内积(\alpha,Y)=(Y,\alpha)=0,且(Y,\alpha)=\alpha^HY=0\\ &\quad AY=(I_n-\frac{2\alpha\alpha^H}{\vert \alpha\vert^2})Y=Y-\frac{2\alpha\alpha^HY}{\vert \alpha\vert^2}=Y \end{aligned}
对于法向量α,Aα=(In−∣α∣22ααH)α=α−∣α∣22ααHα=α−∣α∣22α∣α∣2=−α对于Y∈镜面,有α⊥Y,即内积(α,Y)=(Y,α)=0,且(Y,α)=αHY=0AY=(In−∣α∣22ααH)Y=Y−∣α∣22ααHY=Y
8.4.3 性质
a. 特根
镜面阵至少有两个特征向量 α \alpha α 与 Y Y Y
- A α = − α A\alpha=-\alpha Aα=−α ,特根为 − 1 -1 −1
- A Y = Y AY=Y AY=Y ,特根为 1 1 1
代数方法求特根
平移法:
A
−
I
=
−
2
α
α
H
∣
α
∣
2
为秩
1
矩阵
,
特根
λ
(
A
−
I
)
=
{
−
2
∣
α
∣
2
t
r
(
α
α
H
)
,
0
,
⋯
,
0
⏟
n
−
1
}
=
=
t
r
(
X
X
H
)
=
X
H
X
=
∣
X
∣
2
{
−
2
,
0
,
⋯
,
0
}
⇒
λ
(
A
)
=
λ
(
−
2
α
α
H
∣
α
∣
2
)
+
1
=
{
−
1
,
1
,
⋯
,
1
⏟
n
−
1
}
\begin{aligned} &平移法:\\ &A-I=-2\frac{\alpha\alpha^H}{\vert \alpha\vert^2}为秩1矩阵,\\ &特根\lambda(A-I)=\{\frac{-2}{\vert \alpha\vert^2}tr(\alpha\alpha^H),\underbrace{0,\cdots,0}_{n-1}\}=\xlongequal{tr(XX^H)=X^HX=\vert X\vert^2}\{-2,0,\cdots,0\}\\ &\Rightarrow \lambda(A)=\lambda\left(-2\frac{\alpha\alpha^H}{\vert \alpha\vert^2}\right)+1=\{-1,\underbrace{1,\cdots,1}_{n-1}\} \end{aligned}
平移法:A−I=−2∣α∣2ααH为秩1矩阵,特根λ(A−I)={∣α∣2−2tr(ααH),n−1
0,⋯,0}=tr(XXH)=XHX=∣X∣2{−2,0,⋯,0}⇒λ(A)=λ(−2∣α∣2ααH)+1={−1,n−1
1,⋯,1}
特征多项式
∣
λ
I
−
A
∣
=
(
λ
+
1
)
(
λ
−
1
)
n
−
1
\vert \lambda I-A\vert=(\lambda+1)(\lambda-1)^{n-1}
∣λI−A∣=(λ+1)(λ−1)n−1
b. 特向
镜面上有 n − 1 n-1 n−1 个独立的(线性无关)向量, Y 1 , Y 2 , ⋯ , Y n − 1 Y_1,Y_2,\cdots,Y_{n-1} Y1,Y2,⋯,Yn−1 ( A Y 1 = Y 1 , A Y 2 = Y 2 , ⋯ , A Y n − 1 = Y n − 1 ) (AY_1=Y_1,AY_2=Y_2,\cdots,AY_{n-1}=Y_{n-1}) (AY1=Y1,AY2=Y2,⋯,AYn−1=Yn−1) 都是 1 1 1 的特向
-
Y 1 , Y 2 , ⋯ , Y n − 1 Y_1,Y_2,\cdots,Y_{n-1} Y1,Y2,⋯,Yn−1 为 α H X = 0 \alpha^HX=0 αHX=0 的 n − 1 n-1 n−1 个线性无关的解
证明:
A − I = − 2 ∣ α ∣ 2 α α H 为秩 1 矩阵,故 α 为 A − I 的特向, r ( α H ) = 1 , α H X = 0 且 n − r ( α H ) = n − 1 , 故 α H X = 0 有 n − 1 个线性无关解 Y 1 , ⋯ , Y n − 1 ( A − I ) X = ( − 2 ∣ α ∣ 2 α α H ) X = ( − 2 ∣ α ∣ 2 α ) α H X = 0 ⇒ Y 1 , ⋯ , Y n − 1 为 ( A − I ) 特根为 0 的根 由平移矩阵性质, A − I 与 A 有相同的特根, α , Y 1 , ⋯ , Y n − 1 为 A 的特征向量 ( A − I ) α = − 2 α ⇒ A α = − α ( A − I ) Y 1 = 0 , ⋯ , ( A − I ) Y n − 1 = 0 ⇒ A Y 1 = Y 1 , ⋯ , A Y n − 1 = Y n − 1 \begin{aligned} &A-I=\frac{-2}{\vert \alpha\vert^2}\alpha\alpha^H 为秩1矩阵,故\alpha为A-I的特向,r(\alpha^H)=1,\alpha^HX=0\\ &且n-r(\alpha^H)=n-1,故 \alpha^HX=0有n-1个线性无关解Y_1,\cdots,Y_{n-1}\\ &(A-I)X=(\frac{-2}{\vert \alpha\vert^2}\alpha\alpha^H)X=(\frac{-2}{\vert \alpha\vert^2}\alpha)\alpha^HX=0\Rightarrow Y_1,\cdots,Y_{n-1}为(A-I)特根为0的根\\ &由平移矩阵性质,A-I与A有相同的特根,\alpha,Y_1,\cdots,Y_{n-1}为A的特征向量\\ &(A-I)\alpha=-2\alpha\Rightarrow A\alpha=-\alpha\\ &(A-I)Y_1=0,\cdots,(A-I)Y_{n-1}=0\Rightarrow AY_1=Y_1,\cdots,AY_{n-1}=Y_{n-1} \end{aligned} A−I=∣α∣2−2ααH为秩1矩阵,故α为A−I的特向,r(αH)=1,αHX=0且n−r(αH)=n−1,故αHX=0有n−1个线性无关解Y1,⋯,Yn−1(A−I)X=(∣α∣2−2ααH)X=(∣α∣2−2α)αHX=0⇒Y1,⋯,Yn−1为(A−I)特根为0的根由平移矩阵性质,A−I与A有相同的特根,α,Y1,⋯,Yn−1为A的特征向量(A−I)α=−2α⇒Aα=−α(A−I)Y1=0,⋯,(A−I)Yn−1=0⇒AY1=Y1,⋯,AYn−1=Yn−1
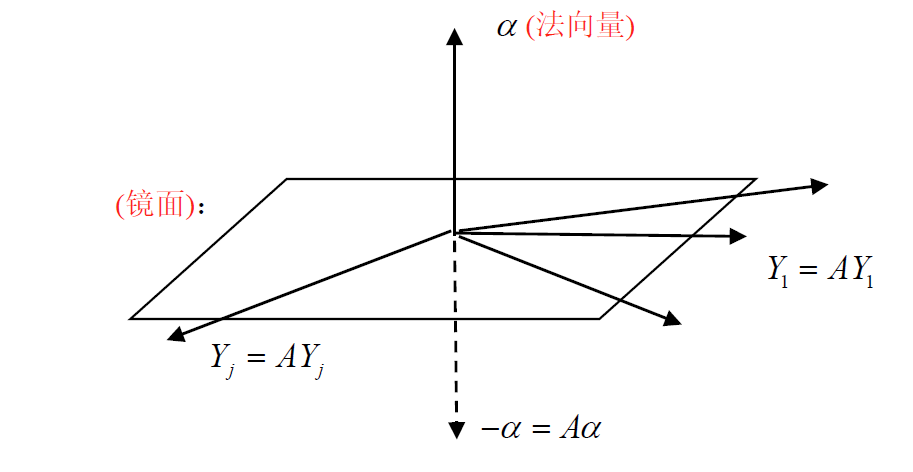
-
镜面阵内 n − 1 n-1 n−1 个特征向量有不同选法,可取 Y 1 ⊥ Y 2 ⊥ ⋯ ⊥ Y n − 1 Y_1\bot Y_2\bot\cdots\bot Y_{n-1} Y1⊥Y2⊥⋯⊥Yn−1 (互正交),故可对镜面阵有 n n n 个正交特向 { X ⊥ Y 1 ⊥ Y 2 ⊥ ⋯ ⊥ Y n − 1 } \{X\bot Y_1\bot Y_2\bot \cdots \bot Y_{n-1}\} {X⊥Y1⊥Y2⊥⋯⊥Yn−1}
正规阵,Hermite阵有 n n n 个相互正交的向量
A A A 的全体特根为 λ ( A ) = { − 1 , 1 , ⋯ , 1 ⏟ n − 1 个 1 } \lambda(A)=\{-1,\underbrace{1,\cdots,1}_{n-1个1}\} λ(A)={−1,n−1个1 1,⋯,1}
c. 镜面阵为 H e r m i t e Hermite Hermite 阵
A = I n − 2 ( α α H ) ∣ α ∣ 2 A=I_n-\frac{2(\alpha\alpha^H)}{\vert \alpha\vert^2} A=In−∣α∣22(ααH) Hermite阵的差
d. A 2 = I A^2=I A2=I
A 2 α = A ( A α ) = A ( − α ) = − ( A α ) = − ( − α ) = α A^2\alpha=A(A\alpha)=A(-\alpha)=-(A\alpha)=-(-\alpha)=\alpha A2α=A(Aα)=A(−α)=−(Aα)=−(−α)=α
即证明: A 2 = I A^2=I A2=I
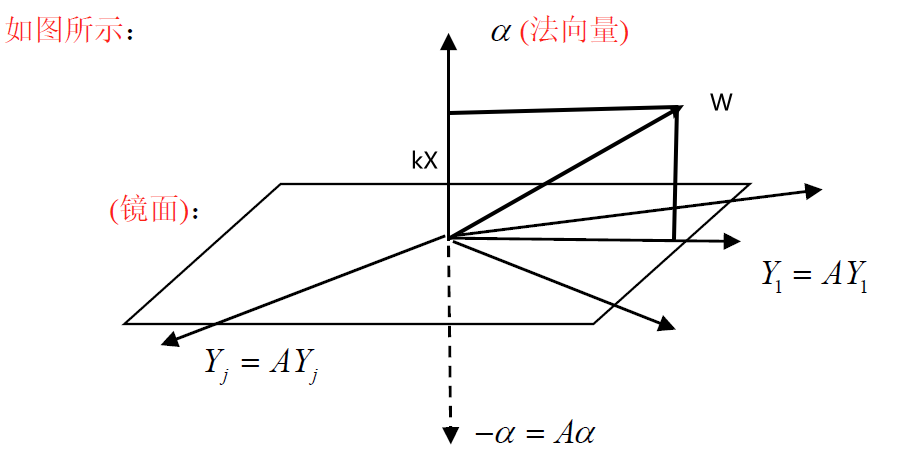
任取 C n 中向量 W , 可分解为 W = Y + k α ( 直角分解 ) A W = A ( Y + k α ) = A Y + k ( A α ) = Y + k ( − α ) = Y − k α = W ~ A 2 W = A ( A W ) = A W ~ = A ( Y − k α ) = A Y − k A α = Y + k α = W ∀ W ∈ C n ,有 A 2 W = W , 故 A 2 = I \begin{aligned} &任取C^n中向量W,可分解为 W=Y+k\alpha(直角分解)\\ &AW=A(Y+k\alpha)=AY+k(A\alpha)=Y+k(-\alpha)=Y-k\alpha=\widetilde{W}\\ &A^2W=A(AW)=A\widetilde{W}=A(Y-k\alpha)=AY-kA\alpha=Y+k\alpha=W\\ &\forall W\in C^n,有A^2W=W,故 A^2=I \end{aligned} 任取Cn中向量W,可分解为W=Y+kα(直角分解)AW=A(Y+kα)=AY+k(Aα)=Y+k(−α)=Y−kα=W A2W=A(AW)=AW =A(Y−kα)=AY−kAα=Y+kα=W∀W∈Cn,有A2W=W,故A2=I
A 2 = ( I − 2 α α H ∣ α ∣ 2 ) 2 = I 2 − 4 α α H ∣ α ∣ 2 + 4 ∣ α ∣ 4 ( α α H ) 2 其中 ( α α H ) 2 = ( α α H ) ( α α H ) = α ( α H α ) α H = ∣ α ∣ 2 α α H ⇒ A 2 = I 2 − 4 α α H ∣ α ∣ 2 + 4 ∣ α ∣ 4 ( α α H ) 2 = I 2 − 4 α α H ∣ α ∣ 2 + 4 ∣ α ∣ 4 ∣ α ∣ 2 α α H = I \begin{aligned} &A^2=\left(I-\frac{2\alpha\alpha^H}{\vert \alpha\vert^2}\right)^2=I^2-\frac{4\alpha\alpha^H}{\vert \alpha\vert^2}+\frac{4}{\vert \alpha\vert^4}\left(\alpha\alpha^H\right)^2\\ &其中 (\alpha\alpha^H)^2=(\alpha\alpha^H)(\alpha\alpha^H)=\alpha(\alpha^H\alpha)\alpha^H=\vert \alpha\vert^2\alpha\alpha^H\\ &\Rightarrow A^2=I^2-\frac{4\alpha\alpha^H}{\vert \alpha\vert^2}+\frac{4}{\vert \alpha\vert^4}\left(\alpha\alpha^H\right)^2=I^2-\frac{4\alpha\alpha^H}{\vert \alpha\vert^2}+\frac{4}{\vert \alpha\vert^4}\vert \alpha\vert^2\alpha\alpha^H=I \end{aligned} A2=(I−∣α∣22ααH)2=I2−∣α∣24ααH+∣α∣44(ααH)2其中(ααH)2=(ααH)(ααH)=α(αHα)αH=∣α∣2ααH⇒A2=I2−∣α∣24ααH+∣α∣44(ααH)2=I2−∣α∣24ααH+∣α∣44∣α∣2ααH=I
d. A − 1 = A A^{-1}=A A−1=A
e. A A A 为优阵
由于 A H = A A^H=A AH=A ,且 A − 1 = A A^{-1}=A A−1=A ,故 A H A = A − 1 A = I A^HA=A^{-1}A=I AHA=A−1A=I , A A A 为优阵
特根 λ ( A ) = { − 1 , 1 , ⋯ , 1 ⏟ n − 1 } \lambda(A)=\{-1,\underbrace{1,\cdots,1}_{n-1}\} λ(A)={−1,n−1 1,⋯,1} ,特向 α ⊥ Y 1 ⊥ ⋯ ⊥ Y n − 1 \alpha\bot Y_1\bot\cdots\bot Y_{n-1} α⊥Y1⊥⋯⊥Yn−1 ,优阵 Q = ( α ∣ α ∣ , Y 1 ∣ Y 1 ∣ , ⋯ , Y n − 1 ∣ Y n − 1 ∣ ) Q=\left(\frac{\alpha}{\vert \alpha\vert},\frac{Y_1}{\vert Y_1\vert},\cdots,\frac{Y_{n-1}}{\vert Y_{n-1}\vert}\right) Q=(∣α∣α,∣Y1∣Y1,⋯,∣Yn−1∣Yn−1) , Q − 1 = Q H Q^{-1}=Q^H Q−1=QH
⇒ Q − 1 A Q = Q H A Q = D = ( − 1 1 ⋱ 1 ) \Rightarrow Q^{-1}AQ=Q^HAQ=D=\left(\begin{matrix}-1&&&\\&1&&\\&&\ddots&\\&&&1\end{matrix}\right) ⇒Q−1AQ=QHAQ=D= −11⋱1 为对角阵
D = ( − 1 1 ⋱ 1 ) D=\left(\begin{matrix}-1&&&\\&1&&\\&&\ddots&\\&&&1\end{matrix}\right) D= −11⋱1 为一个特殊镜面阵,法向量指向 x x x 轴方向
8.4.3 向量构造镜面阵
设 R n R^n Rn 中2个 实向量, α = ( a 1 ⋮ a n ) , β = ( b 1 ⋮ b n ) ∈ R n \alpha=\left(\begin{matrix}a_1\\\vdots\\a_n\end{matrix}\right),\beta=\left(\begin{matrix}b_1\\\vdots\\b_n\end{matrix}\right)\in R^n α= a1⋮an ,β= b1⋮bn ∈Rn ,且 { ∣ α ∣ = ∣ β ∣ α ≠ β \left\{ \begin{aligned}&\vert\alpha\vert=\vert\beta\vert\\&\alpha\neq \beta\end{aligned}\right. {∣α∣=∣β∣α=β ,则有镜面阵 P = I − 2 ( α − β ) ( α − β ) H ∣ ( α − β ) ∣ 2 P=I-\frac{2(\alpha-\beta)(\alpha-\beta)^H}{\vert (\alpha-\beta)\vert^2} P=I−∣(α−β)∣22(α−β)(α−β)H ,使得 P α = β , P β = α P\alpha=\beta,P\beta=\alpha Pα=β,Pβ=α
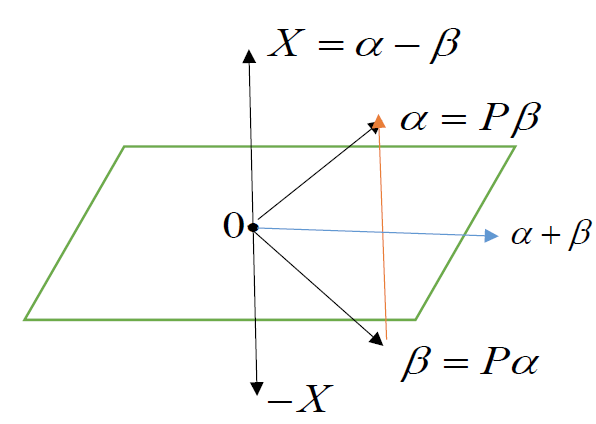
证明:
令
P
=
I
−
2
(
α
−
β
)
(
α
−
β
)
H
∣
(
α
−
β
)
∣
2
⇒
P
X
=
P
(
α
−
β
)
=
(
α
−
β
)
−
2
(
α
−
β
)
(
α
−
β
)
H
(
α
−
β
)
∣
(
α
−
β
)
∣
2
=
−
(
α
−
β
)
=
−
X
(
α
+
β
,
X
)
=
(
α
+
β
,
α
−
β
)
=
(
α
,
α
)
−
(
α
,
β
)
+
(
β
,
α
)
−
(
β
,
β
)
=
∣
α
∣
2
−
∣
β
∣
2
=
0
⇒
法向量
(
α
−
β
)
⊥
(
α
+
β
)
,
其中
(
α
+
β
)
∈
镜面
由于
{
P
(
α
−
β
)
=
−
(
α
−
β
)
P
(
α
+
β
)
=
(
α
+
β
)
,两式相加得
2
P
α
=
2
β
⇒
P
α
=
β
,
P
−
1
β
=
P
β
=
α
\begin{aligned} &令P=I-\frac{2(\alpha-\beta)(\alpha-\beta)^H}{\vert (\alpha-\beta)\vert^2}\\ &\Rightarrow PX=P(\alpha-\beta)=(\alpha-\beta)-2\frac{(\alpha-\beta)(\alpha-\beta)^H(\alpha-\beta)}{\vert (\alpha-\beta)\vert^2}=-(\alpha-\beta)=-X\\ &(\alpha+\beta,X)=(\alpha+\beta,\alpha-\beta)=(\alpha,\alpha)-(\alpha,\beta)+(\beta,\alpha)-(\beta,\beta)=\vert \alpha\vert^2-\vert \beta\vert^2=0\\ &\Rightarrow 法向量 (\alpha-\beta)\bot (\alpha+\beta),其中(\alpha+\beta)\in 镜面\\ &由于\left\{ \begin{aligned} &P(\alpha-\beta)=-(\alpha-\beta)\\ &P(\alpha+\beta)=(\alpha+\beta) \end{aligned} \right.,两式相加得2P\alpha=2\beta\Rightarrow P\alpha=\beta,P^{-1}\beta=P\beta=\alpha \end{aligned}
令P=I−∣(α−β)∣22(α−β)(α−β)H⇒PX=P(α−β)=(α−β)−2∣(α−β)∣2(α−β)(α−β)H(α−β)=−(α−β)=−X(α+β,X)=(α+β,α−β)=(α,α)−(α,β)+(β,α)−(β,β)=∣α∣2−∣β∣2=0⇒法向量(α−β)⊥(α+β),其中(α+β)∈镜面由于{P(α−β)=−(α−β)P(α+β)=(α+β),两式相加得2Pα=2β⇒Pα=β,P−1β=Pβ=α
eg

8.4.4 镜面阵与QR分解
P
x
P_{x}
Px 表示
x
x
x 阶镜面阵 ,
A
x
A_{x}
Ax 表示
x
x
x 阶方阵
P
n
A
n
=
P
n
(
α
1
,
α
2
,
⋯
,
α
n
)
=
P
n
α
1
=
(
μ
1
0
⋮
0
)
n
(
μ
1
∗
O
A
n
−
1
)
(
1
0
0
P
n
−
1
)
P
n
A
n
=
(
1
0
0
P
n
−
1
)
(
μ
1
∗
0
A
n
−
1
)
=
(
μ
1
∗
0
P
n
−
1
A
n
−
1
)
=
(
μ
1
∗
0
P
n
−
1
(
β
1
,
⋯
,
β
n
−
1
)
n
−
1
×
n
−
1
)
=
P
2
β
1
=
(
μ
2
0
⋮
0
)
n
−
1
(
μ
1
∗
∗
0
μ
2
∗
0
0
A
n
−
2
)
\begin{aligned} P_nA_n&=P_n(\alpha_1,\alpha_2,\cdots,\alpha_n)\xlongequal{P_n\alpha_1=\left(\begin{matrix}\mu_1\\0\\\vdots\\0\end{matrix}\right)_n}\left( \begin{matrix} \mu_1&*\\ O&A_{n-1} \end{matrix} \right)\\\\ \left( \begin{matrix} 1&0\\0&P_{n-1} \end{matrix} \right)P_nA_n&=\left( \begin{matrix} 1&0\\0&P_{n-1} \end{matrix} \right)\left( \begin{matrix} \mu_1&*\\ 0&A_{n-1} \end{matrix} \right)= \left( \begin{matrix} \mu_1&*\\ 0&P_{n-1}A_{n-1} \end{matrix} \right)\\ &=\left( \begin{matrix} \mu_1&*\\ 0&P_{n-1}(\beta_1,\cdots,\beta_{n-1})_{n-1\times n-1 } \end{matrix} \right)\\ &\xlongequal{P_2\beta_1=\left(\begin{matrix}\mu_2\\0\\\vdots\\0\end{matrix}\right)_{n-1}}\left( \begin{matrix} \mu_1&*&*\\ 0&\mu_2&*\\ 0&0&A_{n-2} \end{matrix} \right) \end{aligned}
PnAn(100Pn−1)PnAn=Pn(α1,α2,⋯,αn)Pnα1=
μ10⋮0
n(μ1O∗An−1)=(100Pn−1)(μ10∗An−1)=(μ10∗Pn−1An−1)=(μ10∗Pn−1(β1,⋯,βn−1)n−1×n−1)P2β1=
μ20⋮0
n−1
μ100∗μ20∗∗An−2
( 1 0 0 ⋯ 0 0 1 0 ⋯ 0 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ P 2 ) ⋯ ( 1 0 0 P n − 1 ) P n A = ( 1 0 0 ⋯ 0 0 1 0 ⋯ 0 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ P 2 ) ( μ 1 ∗ ∗ ⋯ ∗ 0 μ 2 ∗ ⋯ ∗ 0 0 μ 3 ⋯ ∗ ⋮ ⋮ ⋮ ⋱ ∗ 0 0 0 ⋯ A 2 ) = ( μ 1 ∗ ∗ ⋯ ∗ 0 μ 2 ∗ ⋯ ∗ 0 0 μ 3 ⋯ ∗ ⋮ ⋮ ⋮ ⋱ ∗ 0 0 0 ⋯ P 2 A 2 ) = ( μ 1 ∗ ∗ ⋯ ∗ 0 μ 2 ∗ ⋯ ∗ 0 0 μ 3 ⋯ ∗ ⋮ ⋮ ⋮ ⋱ ∗ 0 0 0 ⋯ P 2 ( γ 1 , γ 2 ) 2 × 2 ) = P 2 γ 1 = ( μ n − 1 0 ) ( μ 1 ∗ ∗ ⋯ ∗ ∗ 0 μ 2 ∗ ⋯ ∗ ∗ 0 0 μ 3 ⋯ ∗ ∗ ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 0 ⋯ μ n − 1 ⋮ 0 0 0 ⋯ 0 ∗ ) = R \begin{aligned} \left( \begin{matrix} 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ 0&0&1&\cdots&0\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\cdots&P_{2} \end{matrix} \right)\cdots\left( \begin{matrix} 1&0\\ 0&P_{n-1} \end{matrix} \right)P_nA&=\left( \begin{matrix} 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ 0&0&1&\cdots&0\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\cdots&P_{2} \end{matrix} \right) \left( \begin{matrix} \mu_1&*&*&\cdots&*\\ 0&\mu_2&*&\cdots&*\\ 0&0&\mu_3&\cdots&*\\ \vdots&\vdots&\vdots&\ddots&*\\ 0&0&0&\cdots&A_{2} \end{matrix} \right)\\ &=\left( \begin{matrix} \mu_1&*&*&\cdots&*\\ 0&\mu_2&*&\cdots&*\\ 0&0&\mu_3&\cdots&*\\ \vdots&\vdots&\vdots&\ddots&*\\ 0&0&0&\cdots&P_{2}A_{2} \end{matrix} \right)\\ &=\left( \begin{matrix} \mu_1&*&*&\cdots&*\\ 0&\mu_2&*&\cdots&*\\ 0&0&\mu_3&\cdots&*\\ \vdots&\vdots&\vdots&\ddots&*\\ 0&0&0&\cdots&P_{2}(\gamma_1,\gamma_2)_{2\times 2} \end{matrix} \right)\\ &\xlongequal{P_2\gamma_1=\left(\begin{matrix}\mu_{n-1}\\0\end{matrix}\right)}\left( \begin{matrix} \mu_1&*&*&\cdots&*&*\\ 0&\mu_2&*&\cdots&*&*\\ 0&0&\mu_3&\cdots&*&*\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&\cdots&\mu_{n-1}&\vdots\\ 0&0&0&\cdots&0&* \end{matrix} \right)=R\\ \end{aligned} 100⋮0010⋮0001⋮0⋯⋯⋯⋱⋯000⋮P2 ⋯(100Pn−1)PnA= 100⋮0010⋮0001⋮0⋯⋯⋯⋱⋯000⋮P2 μ100⋮0∗μ20⋮0∗∗μ3⋮0⋯⋯⋯⋱⋯∗∗∗∗A2 = μ100⋮0∗μ20⋮0∗∗μ3⋮0⋯⋯⋯⋱⋯∗∗∗∗P2A2 = μ100⋮0∗μ20⋮0∗∗μ3⋮0⋯⋯⋯⋱⋯∗∗∗∗P2(γ1,γ2)2×2 P2γ1=(μn−10) μ100⋮00∗μ20⋮00∗∗μ3⋮00⋯⋯⋯⋱⋯⋯∗∗∗⋮μn−10∗∗∗⋮⋮∗ =R
故有镜面阵 Q = P n ( 1 0 0 P n − 1 ) ⋯ ( 1 0 0 ⋯ 0 0 1 0 ⋯ 0 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ P 2 ) Q=P_n\left( \begin{matrix} 1&0\\ 0&P_{n-1} \end{matrix} \right)\cdots\left( \begin{matrix} 1&0&0&\cdots&0\\ 0&1&0&\cdots&0\\ 0&0&1&\cdots&0\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\cdots&P_{2} \end{matrix} \right) Q=Pn(100Pn−1)⋯ 100⋮0010⋮0001⋮0⋯⋯⋯⋱⋯000⋮P2 ,使 Q A = R QA=R QA=R ,由于镜面阵为优H阵 Q H = Q − 1 = Q Q^H=Q^{-1}=Q QH=Q−1=Q ,故有 Q R QR QR 分解 A = Q R A=QR A=QR
2阶例题

令 α = ( 1 i ) , ∣ α ∣ = 2 ,令 β = ( 2 0 ) , 令镜面法向量 X = α − β = ( 1 − 2 i ) X X H = ( 1 − 2 i ) ( 1 − 2 − i ) = ( ( 1 − 2 ) 2 − i ( 1 − 2 ) i ( 1 − 2 ) 1 ) = ( 3 − 2 − i ( 1 − 2 ) i ( 1 − 2 ) 1 ) ∣ X ∣ 2 = X H X = ( 1 − 2 − i ) ( 1 − 2 i ) = 2 ( 2 − 2 ) 镜面阵 Q = I 2 − 2 X X H ∣ X ∣ 2 = ( 1 0 0 1 ) − 2 2 ( 2 − 2 ) ( 3 − 2 2 − i ( 1 − 2 ) i ( 1 − 2 ) 1 ) = 1 2 ( 1 − i i − 1 ) 使得 Q ( 1 i ) = ( 2 0 ) ⇒ Q A = Q ( α 1 , α 2 ) = ( Q α 1 , Q α 2 ) = ( 2 i 2 0 − 3 2 ) = R 解出 A 的 Q R 分解 A = Q R , Q = 1 2 ( 1 − i i − 1 ) \begin{aligned} &令\alpha=\left( \begin{matrix} 1\\i \end{matrix} \right),\vert\alpha\vert=\sqrt{2},令 \beta=\left( \begin{matrix} \sqrt{2}\\0 \end{matrix} \right),令镜面法向量X=\alpha-\beta=\left( \begin{matrix} 1-\sqrt{2}\\i \end{matrix} \right)\\ &XX^H=\left( \begin{matrix} 1-\sqrt{2}\\i \end{matrix} \right)\left(1-\sqrt{2}\quad -i\right)=\left(\begin{matrix} (1-\sqrt{2})^2&-i(1-\sqrt{2})\\ i(1-\sqrt2)&1 \end{matrix}\right)=\left( \begin{matrix} 3-\sqrt{2}&-i(1-\sqrt{2})\\ i(1-\sqrt{2})&1 \end{matrix} \right)\\ &\vert X\vert^2=X^HX=\left( \begin{matrix} 1-\sqrt{2}\quad -i \end{matrix} \right)\left( \begin{matrix} 1-\sqrt{2}\\i \end{matrix} \right)=2(2-\sqrt{2})\\ &镜面阵Q=I_2-2\frac{XX^H}{\vert X\vert^2}=\left( \begin{matrix} 1&0\\0&1 \end{matrix} \right)-\frac{2}{2(2-\sqrt{2})}\left( \begin{matrix} 3-2\sqrt{2}&-i(1-\sqrt{2})\\ i(1-\sqrt{2})&1 \end{matrix} \right)=\frac{1}{\sqrt{2}}\left( \begin{matrix} 1&-i\\i&-1 \end{matrix} \right)\\ &使得 Q\left( \begin{matrix} 1\\i \end{matrix} \right)=\left( \begin{matrix} \sqrt{2}\\0 \end{matrix} \right)\Rightarrow QA=Q(\alpha_1,\alpha_2)=\left(Q\alpha_1,Q\alpha_2\right)=\left( \begin{matrix} \sqrt{2}&\frac{i}{\sqrt{2}}\\ 0&-\frac{3}{\sqrt{2}} \end{matrix} \right)=R\\ &解出A的QR分解 A=QR,Q=\frac{1}{\sqrt{2}}\left( \begin{matrix} 1&-i\\i&-1 \end{matrix} \right) \end{aligned} 令α=(1i),∣α∣=2,令β=(20),令镜面法向量X=α−β=(1−2i)XXH=(1−2i)(1−2−i)=((1−2)2i(1−2)−i(1−2)1)=(3−2i(1−2)−i(1−2)1)∣X∣2=XHX=(1−2−i)(1−2i)=2(2−2)镜面阵Q=I2−2∣X∣2XXH=(1001)−2(2−2)2(3−22i(1−2)−i(1−2)1)=21(1i−i−1)使得Q(1i)=(20)⇒QA=Q(α1,α2)=(Qα1,Qα2)=(202i−23)=R解出A的QR分解A=QR,Q=21(1i−i−1)
3阶例题
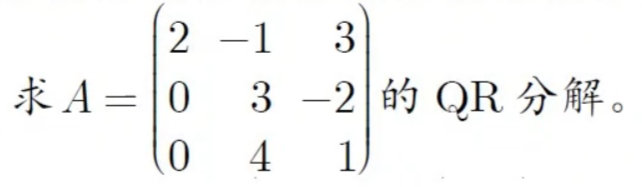
令 P 3 = I , P 3 ( 2 0 0 ) = ( 2 0 0 ) , 使得 P 3 A = ( 2 ∗ 0 A 2 ) 令 α 2 = ( 3 4 ) , β 2 = ( ∣ α 2 ∣ 0 ) = ( 5 0 ) , 二维镜面法向量 X 2 = α 2 − β 2 = ( − 2 4 ) , ∣ X 2 ∣ 2 = 20 , X X H = ( 5 − 8 − 8 16 ) P 2 = I 2 − 2 ∣ X 2 ∣ 2 X X H = ( 3 5 4 5 4 5 − 3 5 ) , 使得 P 2 A 2 = ( 5 − 2 5 0 − 11 5 ) ⇒ ( 1 0 0 P 2 ) P 3 A = ( 1 0 0 0 3 5 4 5 0 4 5 − 3 5 ) A = R = ( 2 − 1 3 0 3 5 − 2 5 0 0 − 11 5 ) 故有 Q = ( 1 0 0 P 2 ) P 3 = ( 1 0 0 0 3 5 4 5 0 4 5 − 3 5 ) , R = ( 2 − 1 3 0 3 5 − 2 5 0 0 − 11 5 ) , 使得 A = Q R \begin{aligned} &令P_3=I,P_3\left( \begin{matrix} 2\\0\\0 \end{matrix} \right)=\left( \begin{matrix} 2\\0\\0 \end{matrix} \right),使得P_3A=\left( \begin{matrix} 2&*\\ 0&A_2 \end{matrix} \right)\\ &令\alpha_2=\left( \begin{matrix} 3\\4 \end{matrix} \right),\beta_2=\left( \begin{matrix} \vert \alpha_2\vert\\0 \end{matrix} \right)=\left( \begin{matrix} 5\\0 \end{matrix} \right),二维镜面法向量X_2=\alpha_2-\beta_2=\left( \begin{matrix} -2\\4 \end{matrix} \right),\vert X_2\vert^2=20,XX^H=\left( \begin{matrix} 5&-8\\-8&16 \end{matrix} \right)\\ &\quad P_2=I_2-\frac{2}{\vert X_2\vert^2}XX^H=\left( \begin{matrix} \frac{3}{5}&\frac{4}{5}\\\frac{4}{5}&-\frac{3}{5} \end{matrix} \right),使得P_2A_2=\left( \begin{matrix} 5&-\frac{2}{5}\\0&-\frac{11}{5} \end{matrix} \right)\\ &\Rightarrow\left( \begin{matrix} 1&0\\0&P_2 \end{matrix} \right)P_3A=\left( \begin{matrix} 1&0&0\\ 0&\frac{3}{5}&\frac{4}{5}\\ 0&\frac{4}{5}&-\frac{3}{5} \end{matrix} \right)A=R=\left( \begin{matrix} 2&-1&3\\ 0&\frac{3}{5}&-\frac{2}{5}\\ 0&0&-\frac{11}{5} \end{matrix} \right)\\ &故有Q=\left( \begin{matrix} 1&0\\ 0&P_2 \end{matrix} \right)P_3=\left( \begin{matrix} 1&0&0\\ 0&\frac{3}{5}&\frac{4}{5}\\ 0&\frac{4}{5}&-\frac{3}{5} \end{matrix} \right),R=\left( \begin{matrix} 2&-1&3\\ 0&\frac{3}{5}&-\frac{2}{5}\\ 0&0&-\frac{11}{5} \end{matrix} \right),使得A=QR \end{aligned} 令P3=I,P3 200 = 200 ,使得P3A=(20∗A2)令α2=(34),β2=(∣α2∣0)=(50),二维镜面法向量X2=α2−β2=(−24),∣X2∣2=20,XXH=(5−8−816)P2=I2−∣X2∣22XXH=(535454−53),使得P2A2=(50−52−511)⇒(100P2)P3A= 10005354054−53 A=R= 200−15303−52−511 故有Q=(100P2)P3= 10005354054−53 ,R= 200−15303−52−511 ,使得A=QR
8.5 正定阵
8.5.1 二次型
a. 二次型定义
令 A A A 为 H e r m i t e Hermite Hermite 阵 ( A H = A ∈ C n × n ) (A^H=A\in C^{n\times n}) (AH=A∈Cn×n), X = ( x 1 x 2 ⋮ x n ) X=\left( \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right) X= x1x2⋮xn ,称 X H A X = ( x 1 ‾ , x 2 ‾ , ⋯ , x n ‾ ) A ( x 1 x 2 ⋮ x n ) X^HAX=\left(\overline{x_1},\overline{x_2},\cdots,\overline{x_n}\right)A\left( \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right) XHAX=(x1,x2,⋯,xn)A x1x2⋮xn ,为矩阵 A A A 产生的二次型,记为 f ( x ) = X H A X f(x)=X^HAX f(x)=XHAX
b. 正定二次型与正定阵定义
若
A
H
=
A
A^H=A
AH=A ,对一切
X
≠
0
X\neq 0
X=0 ,有
X
H
A
X
>
0
X^HAX>0
XHAX>0 ,则
f
(
x
)
=
X
H
A
X
f(x)=X^HAX
f(x)=XHAX 为正定二次型,A为正定阵,记为
A
>
0
A>0
A>0
若
A
H
=
A
A^H=A
AH=A ,对一切
X
≠
0
X\neq 0
X=0 ,有
X
H
A
X
≥
0
X^HAX\ge 0
XHAX≥0 ,则
f
(
x
)
=
X
H
A
X
f(x)=X^HAX
f(x)=XHAX 为半正定二次型,A为半正定阵,记为
A
≥
0
A\ge 0
A≥0
8.5.2 正定阵的定理
A
>
0
⟺
A>0\iff
A>0⟺
A
A
A 为Hermite阵,且
λ
1
,
λ
2
,
⋯
,
λ
n
>
0
\lambda_1,\lambda_2,\cdots,\lambda_n > 0
λ1,λ2,⋯,λn>0
A
≥
0
⟺
A\ge 0 \iff
A≥0⟺
A
A
A 为Hermite阵,且
λ
1
,
λ
2
,
⋯
,
λ
n
≥
0
\lambda_1,\lambda_2,\cdots,\lambda_n \ge 0
λ1,λ2,⋯,λn≥0
证明
⇒ \Rightarrow ⇒
若 A A A 为正定阵,则 A A A 生成的二次型 f ( x ) = X H A X > 0 f(x)=X^HAX>0 f(x)=XHAX>0 , ∴ λ i = X H A X ∣ X ∣ 2 > 0 \therefore \lambda_i=\frac{X^HAX}{\vert X\vert^2}>0 ∴λi=∣X∣2XHAX>0
⇐
\Leftarrow
⇐
由
H
e
r
m
i
t
e
分解定理,
A
为
H
e
r
m
i
t
e
阵,则存在
U
阵
Q
,
使得
Q
H
A
Q
=
Λ
=
(
λ
1
⋱
λ
n
)
∴
A
=
Δ
Λ
,
而
λ
i
>
0
,
Λ
为正定阵,故
A
为正定阵
\begin{aligned} &由Hermite分解定理,A为Hermite阵,则存在U阵Q,\\ &使得Q^HAQ=\Lambda=\left( \begin{matrix} \lambda_1&\quad&\quad\\ &\ddots&\quad\\ &\quad&\lambda_n\\ \end{matrix} \right)\\ &\therefore A\overset{\Delta}{=}\Lambda,而\lambda_i>0,\Lambda 为正定阵,故A为正定阵 \end{aligned}
由Hermite分解定理,A为Hermite阵,则存在U阵Q,使得QHAQ=Λ=
λ1⋱λn
∴A=ΔΛ,而λi>0,Λ为正定阵,故A为正定阵
单位阵是正定阵 :
λ
i
=
1
\lambda_i= 1
λi=1 显然大于0
8.5.3 正定阵间必合同
- A > 0 (正定阵) ⟺ A = Δ Λ A>0(正定阵) \iff A\overset{\Delta}{=}\Lambda A>0(正定阵)⟺A=ΔΛ
- Λ = Δ I \Lambda\overset{\Delta}{=}I Λ=ΔI 对角阵一定合同于单位阵
- 若A,B为同阶正定阵,则 A = Δ B A\overset{\Delta}{=} B A=ΔB
证明1:
若
A
正定,则有
A
H
=
A
由
H
e
r
m
i
t
e
分解定理,必
∃
优阵
Q
使得
Q
H
A
Q
=
Λ
,
且
λ
i
>
0
\begin{aligned} &若A正定,则有A^H=A\\ &由Hermite分解定理,必\exist 优阵Q使得Q^HAQ=\Lambda,且\lambda_i>0\\ \end{aligned}
若A正定,则有AH=A由Hermite分解定理,必∃优阵Q使得QHAQ=Λ,且λi>0
证明2:
若
Λ
=
(
λ
1
⋱
λ
n
)
,
其中
λ
i
>
0
⇒
f
(
x
)
=
X
H
Λ
X
=
λ
1
∣
x
1
∣
2
+
λ
2
∣
x
2
∣
2
+
⋯
+
λ
n
∣
x
n
∣
2
>
0
⇒
可分解为
Λ
=
(
λ
1
⋱
λ
n
)
I
(
λ
1
⋱
λ
n
)
=
P
I
P
可知
P
可逆,且
P
H
=
P
,
故
P
H
I
P
=
Λ
即对角正定阵合同于单位阵,记为
Λ
=
Δ
I
\begin{aligned} 若\Lambda&=\left( \begin{matrix} \lambda_1&\quad&\quad\\ &\ddots&\\ &&\lambda_n \end{matrix} \right),其中\lambda_i>0\\ &\Rightarrow f(x)=X^H\Lambda X=\lambda_1\vert x_1\vert^2+\lambda_2\vert x_2\vert^2+\cdots+\lambda_n\vert x_n\vert^2>0\\ &\Rightarrow 可分解为\Lambda=\left( \begin{matrix} \sqrt{\lambda_1}&\quad&\quad\\ \quad&\ddots&\quad\\ \quad&\quad&\sqrt{\lambda_n}\\ \end{matrix} \right)I\left( \begin{matrix} \sqrt{\lambda_1}&&\\ &\ddots&\\ &&\sqrt{\lambda_n}\\ \end{matrix} \right)\\ &\quad \quad\quad\quad\quad \quad \quad=PIP\\ &可知P可逆,且P^H=P,故P^HIP=\Lambda\\ &即对角正定阵合同于单位阵,记为\Lambda\overset{\Delta}{=}I \end{aligned}
若Λ=
λ1⋱λn
,其中λi>0⇒f(x)=XHΛX=λ1∣x1∣2+λ2∣x2∣2+⋯+λn∣xn∣2>0⇒可分解为Λ=
λ1⋱λn
I
λ1⋱λn
=PIP可知P可逆,且PH=P,故PHIP=Λ即对角正定阵合同于单位阵,记为Λ=ΔI
证明3:
由
A
>
0
,
B
>
0
,
则
A
=
Δ
I
,
B
=
Δ
I
⇒
A
=
Δ
B
\begin{aligned} &由A>0,B>0,则A\overset{\Delta}{=}I,B\overset{\Delta}{=}I\Rightarrow A\overset{\Delta}{=}B \end{aligned}
由A>0,B>0,则A=ΔI,B=ΔI⇒A=ΔB
8.5.4 乘积形式的正定阵
- 对一切矩阵 A = A n × p A=A_{n\times p} A=An×p 且 n ≥ p n\ge p n≥p , A H A A^HA AHA 与 A A H AA^H AAH 都是Hermite阵
- A H A A^HA AHA 与 A A H AA^H AAH 只相差 n − p n-p n−p 个0根
- A H A ≥ 0 A^HA\ge0 AHA≥0 , A H A ≥ 0 A^HA\ge 0 AHA≥0
- r ( A H A ) = r ( A A H ) = r ( A ) r(A^HA)=r(AA^H)=r(A) r(AHA)=r(AAH)=r(A)
a. A H A A^HA AHA 为Hermite阵
( A H A ) H = A H A ,且 ( A A H ) H = A A H ,则 A H A 与 A A H 为 H e r m i t e 阵 \begin{aligned} (A^HA)^H=A^HA,且(AA^H)^H=AA^H,则A^HA与AA^H为Hermite阵 \end{aligned} (AHA)H=AHA,且(AAH)H=AAH,则AHA与AAH为Hermite阵
b. A H A 与 A A H A^HA与AA^H AHA与AAH 相差n-p个0根
A = A n × p , B = p × n , 且 n ≥ p 由换位公式 ∣ λ I − A B ∣ = λ n − p ∣ λ I − B A ∣ , 则 A B 与 B A 必有相同的非零根,故 A H A 与 A A H 只相差 n − p 个零根 \begin{aligned} &A=A_{n\times p},B={p\times n},且n\ge p\\ &由换位公式 \vert \lambda I-AB\vert=\lambda^{n-p}\vert \lambda I-BA \vert,\\ &则 AB与BA必有相同的非零根,故A^HA与AA^H只相差n-p个零根 \end{aligned} A=An×p,B=p×n,且n≥p由换位公式∣λI−AB∣=λn−p∣λI−BA∣,则AB与BA必有相同的非零根,故AHA与AAH只相差n−p个零根
c. A H A 与 A A H A^HA与AA^H AHA与AAH 是半正定阵(不是方阵的正定阵)
对任意非零向量 X ,有二次型 f ( x ) = X H A H A X = ( A X ) H ( A X ) = ∣ A X ∣ 2 ≥ 0 , 可知 f ( x ) 为半正定二次型, A H A 为半正定阵 \begin{aligned} &对任意非零向量X,有二次型f(x)=X^HA^HAX=(AX)^H(AX)=\vert AX \vert^2\ge 0,\\ &可知f(x)为半正定二次型,A^HA为半正定阵 \end{aligned} 对任意非零向量X,有二次型f(x)=XHAHAX=(AX)H(AX)=∣AX∣2≥0,可知f(x)为半正定二次型,AHA为半正定阵
d. r ( A A H ) = r ( A H A ) = r ( A ) r(AA^H)=r(A^HA)=r(A) r(AAH)=r(AHA)=r(A)
由 A H A 为半正定阵,则 A H A 与 A A H 都只有非负根 可写为 λ ( A H A ) = { λ 1 , λ 2 , . . . λ p } ≥ 0 由换位公式,知 λ A H A 与 λ A A H 只相差 n − p 个零根 ∴ λ ( A A H ) = { λ 1 , λ 2 , . . . , λ p , 0 , 0 , . . . , 0 } ≥ 0 r ( A H A ) = r ( A A H ) = p = r ( A ) = r ( A H ) \begin{aligned} &由A^HA为半正定阵,则A^HA与AA^H都只有非负根\\ &可写为\lambda(A^HA)=\{\lambda_1,\lambda_2,...\lambda_p\}\ge 0\\ &由换位公式,知\lambda{A^HA}与\lambda{AA^H}只相差n-p个零根\\ &\therefore \lambda(AA^H)=\{\lambda_1,\lambda_2,...,\lambda_p,0,0,...,0\}\ge 0\\ &r(A^HA)=r(AA^H)=p=r(A)=r(A^H) \end{aligned} 由AHA为半正定阵,则AHA与AAH都只有非负根可写为λ(AHA)={λ1,λ2,...λp}≥0由换位公式,知λAHA与λAAH只相差n−p个零根∴λ(AAH)={λ1,λ2,...,λp,0,0,...,0}≥0r(AHA)=r(AAH)=p=r(A)=r(AH)
齐次方程组 A X = 0 , A H A X = 0 ,解集相同 ( 同解 ) 若 ( A H A ) X = 0 成立,则 ∣ A X ∣ 2 = ( A X ) H ( A X ) = X H A H A X = ( A X ) 2 = 0 ∴ A X = 0 , r ( A H A ) = r ( A ) \begin{aligned} &齐次方程组AX=0,A^HAX=0,解集相同(同解)\\ &若(A^HA)X=0成立,则\vert AX \vert^2=(AX)^H(AX)=X^HA^HAX=(AX)^2=0\\ &\therefore AX=0,r(A^HA)=r(A) \end{aligned} 齐次方程组AX=0,AHAX=0,解集相同(同解)若(AHA)X=0成立,则∣AX∣2=(AX)H(AX)=XHAHAX=(AX)2=0∴AX=0,r(AHA)=r(A)






![[ 数据结构 ] 汉诺塔--------分治算法最佳实践](https://img-blog.csdnimg.cn/img_convert/7d96447a7fb433347f93cdf2b2e4a2cb.png)