1. 题目解析

题目地址：点这里

2. 讲解算法原理

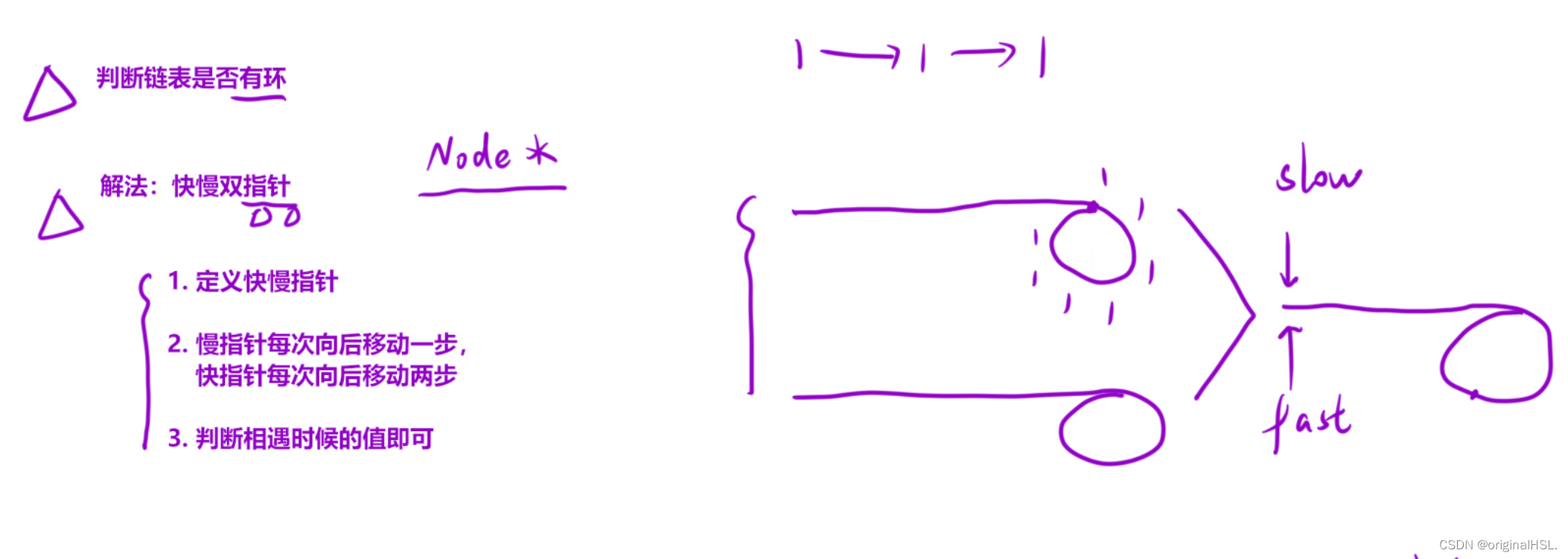
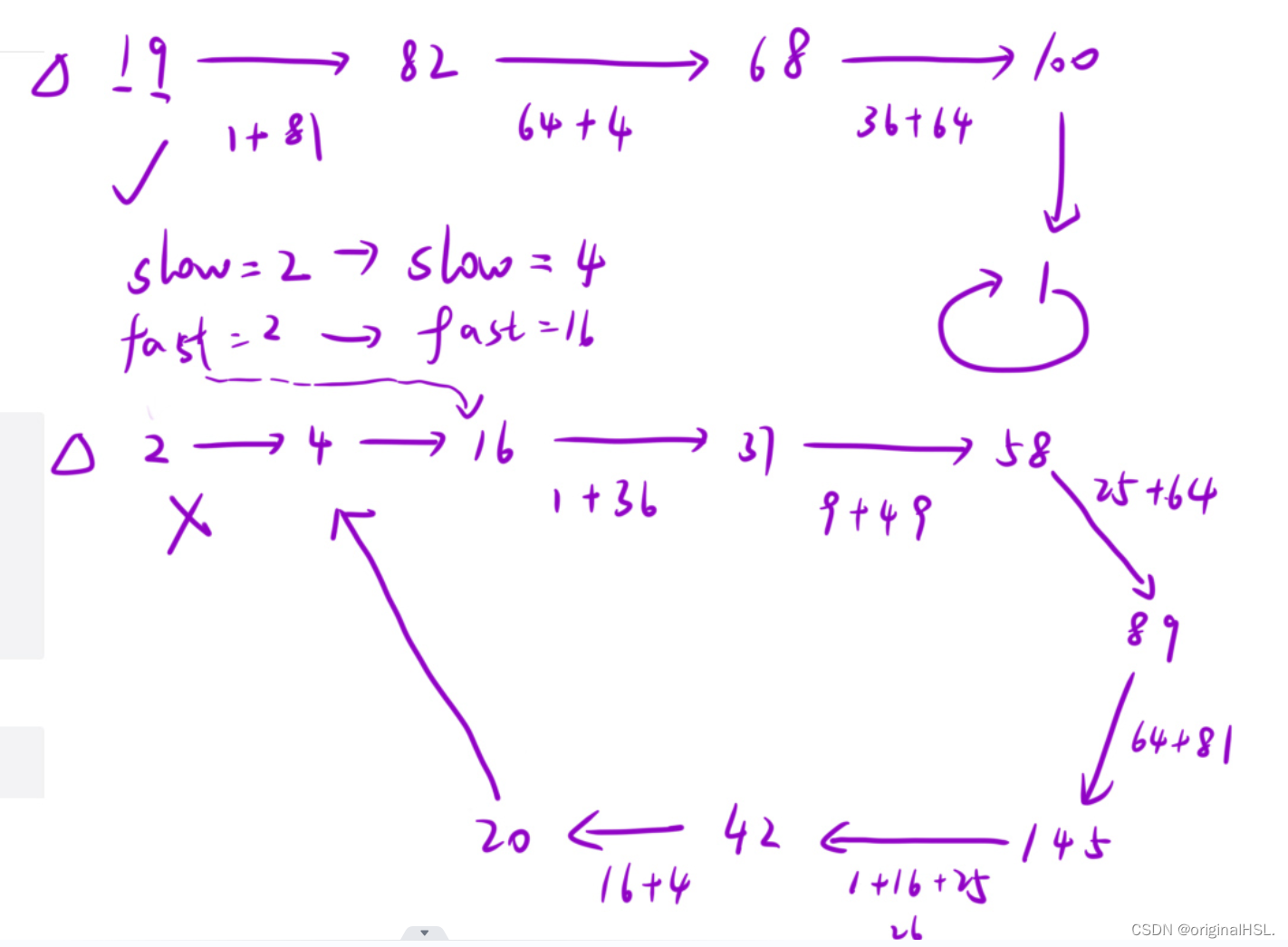
• 本题根据鸽巢原理是一定会有环的，最后要么无限循环1，要么碰到一个不为1的重复数继续循环

鸽巢原理

鸽巢原理（Pigeonhole Principle）是一种基本的数学原理，也被称为抽屉原理（Drawer Principle）或鸽笼原理（Box Principle）。它是指如果有n+1个物体放入n个容器中，那么至少有一个容器中会放入两个或更多的物体。

鸽巢原理的简单表述是：如果将n+1个物体放入n个容器中，那么至少有一个容器中会放入两个或更多的物体。（用在数字中就表示：规定在[0,n]范围内的数，无论如何运算，在运算n+1次后，一定至少会有一次重复）

这个原理的背后思想是，当要将大量的物体放入数量有限的容器中时，如果物体的数量大于容器的数量，那么至少有一个容器必须承载多个物体。

---

算法的基本思路如下：

1.定义两个指针，一个快指针（fast）和一个慢指针（slow）。初始时，将快指针和慢指针都设置为输入的数（n）。

2.在每次迭代中，快指针会通过调用PowSum函数计算得到一个新的值，即将当前值的每个位置上的数字的平方和。然后再次调用PowSum函数得到一个新的值，相当于快指针每次向前移动两步。

3.慢指针在每次迭代中只移动一步，通过调用PowSum函数计算得到一个新的值。

4.在每次迭代后，判断快指针和慢指针是否相等。如果相等，说明找到了一个循环，即存在一个环形路径。如果不相等，继续下一次迭代。

5.当快指针和慢指针相等时，终止循环。此时判断快指针的值是否为1。如果是1，则表示输入的数是快乐数，返回true。如果不是1，则表示输入的数不是快乐数，返回false。

---

3. 编写代码

class Solution {
public:
//整数各位置上数的平方和
    int PowSum(int m)
    {
        int sum=0;
        while(m)
        {
            int x=m%10;
            m/=10;
            sum+=x*x;
        }
        return sum;
    }
    bool isHappy(int n) {
        //根据鸽巢原理，是一定有环的
        int fast=PowSum(n);//快指针
        int slow=n;//慢指针
        //判断俩指针相遇时的值就行
        while(slow!=fast)
        {
            int temp=PowSum(fast);
            fast=PowSum(temp);
            slow=PowSum(slow);
        }
        if(fast==1)
        return true;
        else 
        return false;
    }
};