旨在对b站老王所讲的百度Apollo - EM planner算法做浓缩版总结
0 决策规划背景
基于图搜索
优点:
可以得到全局层面最优解,适用于比较低维数的规划问题
缺点:
规划问题维数较高时,面临指数爆炸问题
基于采样
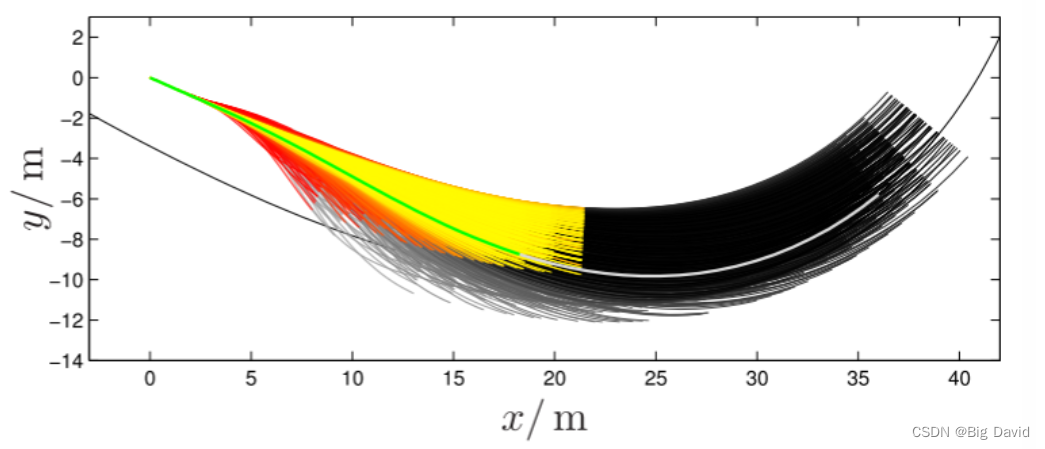
优点:
计算量低,曲率连续,行驶平顺性好
缺点:
曲线通常是四阶或者更高,系数的计算难以使车辆到达确定的运动状态
基于插值的曲率规划
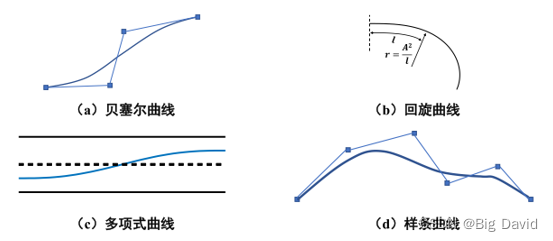
优点:
算法总是可以收敛到满足条件的解,适用于全局规划和局部规划
缺点:
产生的轨迹不连续而且不平稳,路径的最优性受时间影响
基于函数优化
优点:
影响因素考虑多,包含道路限制条件、自车限制,便于处理约束,可以满足不同优化目标,求解速度快
缺点:
最优解一般比较贴近约束,转化为优化问题本身较为困难
自动驾驶总共分成了六个等级:L0 - L5
| 等级 | 详述 |
|---|---|
| L0 | 没有任何自动驾驶功能 |
| L1 | 有横向和纵向的自动驾驶功能,但是横纵向无法联合作用 |
| L2 | 横纵向可以联合作用,但是驾驶员必须对一切情况负责 |
| L3 | 功能和L2基本相同,最大的区别在于责任,对于部分场景,驾驶员不必负责 |
| L4 | 大部分道路皆可自动驾驶,大部分场景都不需要驾驶员负责 |
| L5 | 完全自动驾驶 |
EM Planner是Apollo的经典决策规划算法,擅长处理复杂环境下的决策规划问题。
2 规划需要的背景知识
2.1 五次多项式
- 位置
x ( t ) = a 0 + a 1 t + a 2 t 2 + a 3 t 3 + a 4 t 4 + a 5 t 5 y ( t ) = b 0 + b 1 t + b 2 t 2 + b 3 t 3 + b 4 t 4 + b 5 t 5 x(t) = a_{0}+a_{1}t+a_{2}t^2+a_{3}t^3+a_{4}t^4+a_{5}t^5\\ y(t) = b_{0}+b_{1}t+b_{2}t^2+b_{3}t^3+b_{4}t^4+b_{5}t^5 x(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5y(t)=b0+b1t+b2t2+b3t3+b4t4+b5t5 - 速度
x ˙ ( t ) = a 1 + 2 a 2 t + 3 a 3 t 2 + 4 a 4 t 3 + 5 a 5 t 4 y ˙ ( t ) = b 1 + 2 b 2 t + 3 b 3 t 2 + 4 b 4 t 3 + 5 b 5 t 4 \dot{x} (t)=a_{1}+2a_{2}t+3a_{3}t^2+4a_{4}t^3+5a_{5}t^4\\ \dot{y} (t)=b_{1}+2b_{2}t+3b_{3}t^2+4b_{4}t^3+5b_{5}t^4 x˙(t)=a1+2a2t+3a3t2+4a4t3+5a5t4y˙(t)=b1+2b2t+3b3t2+4b4t3+5b5t4 - 加速度
x ¨ ( t ) = 2 a 2 + 6 a 3 t + 12 a 4 t 2 + 20 a 5 t 3 y ¨ ( t ) = 2 b 2 + 6 b 3 t + 12 b 4 t 2 + 20 b 5 t 3 \ddot{x} (t)=2a_{2}+6a_{3}t+12a_{4}t^2+20a_{5}t^3\\ \ddot{y} (t)=2b_{2}+6b_{3}t+12b_{4}t^2+20b_{5}t^3 x¨(t)=2a2+6a3t+12a4t2+20a5t3y¨(t)=2b2+6b3t+12b4t2+20b5t3
化为矩阵形式。
X
=
[
x
(
0
)
x
(
0
)
˙
x
(
0
)
¨
x
(
T
)
x
(
T
)
˙
x
(
T
)
¨
]
=
[
t
0
5
t
0
4
t
0
3
t
0
2
t
0
1
5
t
0
4
4
t
0
3
3
t
0
2
2
t
0
1
0
20
t
0
3
12
t
0
2
6
t
0
2
0
0
t
1
5
t
1
4
t
1
3
t
1
2
t
1
1
5
t
1
4
4
t
1
3
3
t
1
2
2
t
1
1
0
20
t
1
3
12
t
1
2
6
t
1
2
0
0
]
[
a
5
a
4
a
3
a
2
a
1
a
0
]
=
T
X
A
X=\begin{bmatrix}x(0) \\\dot{x(0)} \\\ddot{x(0)} \\x(T) \\\dot{x(T)} \\\ddot{x(T)} \end{bmatrix}=\begin{bmatrix} t_{0}^5& t_{0}^4 & t_{0}^3 & t_{0}^2 & t_{0} &1 \\ 5t_{0}^4 & 4t_{0}^3 & 3t_{0}^2 & 2t_{0} & 1 & 0\\ 20t_{0}^3 & 12t_{0}^2 & 6t_{0} & 2 & 0 & 0\\ t_{1}^5& t_{1}^4 & t_{1}^3 & t_{1}^2 & t_{1}& 1\\ 5t_{1}^4 & 4t_{1}^3 & 3t_{1}^2 & 2t_{1} & 1 & 0\\ 20t_{1}^3 & 12t_{1}^2 & 6t_{1} & 2 & 0 & 0 \end{bmatrix}\begin{bmatrix}a_{5} \\a_{4} \\a_{3} \\a_{2} \\a_{1} \\a_{0} \end{bmatrix}=TXA
X=
x(0)x(0)˙x(0)¨x(T)x(T)˙x(T)¨
=
t055t0420t03t155t1420t13t044t0312t02t144t1312t12t033t026t0t133t126t1t022t02t122t12t010t110100100
a5a4a3a2a1a0
=TXA
Y
=
[
y
(
0
)
y
(
0
)
˙
y
(
0
)
¨
y
(
T
)
y
(
T
)
˙
y
(
T
)
¨
]
=
[
t
0
5
t
0
4
t
0
3
t
0
2
t
0
1
5
t
0
4
4
t
0
3
3
t
0
2
2
t
0
1
0
20
t
0
3
12
t
0
2
6
t
0
2
0
0
t
1
5
t
1
4
t
1
3
t
1
2
t
1
1
5
t
1
4
4
t
1
3
3
t
1
2
2
t
1
1
0
20
t
1
3
12
t
1
2
6
t
1
2
0
0
]
[
a
5
b
4
b
3
b
2
b
1
b
0
]
=
T
X
B
Y=\begin{bmatrix}y(0) \\\dot{y(0)} \\\ddot{y(0)} \\y(T) \\\dot{y(T)} \\\ddot{y(T)} \end{bmatrix}=\begin{bmatrix} t_{0}^5& t_{0}^4 & t_{0}^3 & t_{0}^2 & t_{0} &1 \\ 5t_{0}^4 & 4t_{0}^3 & 3t_{0}^2 & 2t_{0} & 1 & 0\\ 20t_{0}^3 & 12t_{0}^2 & 6t_{0} & 2 & 0 & 0\\ t_{1}^5& t_{1}^4 & t_{1}^3 & t_{1}^2 & t_{1}& 1\\ 5t_{1}^4 & 4t_{1}^3 & 3t_{1}^2 & 2t_{1} & 1 & 0\\ 20t_{1}^3 & 12t_{1}^2 & 6t_{1} & 2 & 0 & 0 \end{bmatrix}\begin{bmatrix}a_{5} \\b_{4} \\b_{3} \\b_{2} \\b_{1} \\b_{0} \end{bmatrix}=TXB
Y=
y(0)y(0)˙y(0)¨y(T)y(T)˙y(T)¨
=
t055t0420t03t155t1420t13t044t0312t02t144t1312t12t033t026t0t133t126t1t022t02t122t12t010t110100100
a5b4b3b2b1b0
=TXB
X
,
Y
,
T
X,Y,T
X,Y,T已知,就可以求出
A
A
A和
B
B
B。
衡量舒适性的物理量为跃度
J
e
r
k
Jerk
Jerk
J
e
r
k
=
d
a
d
t
{Jerk = \frac{da}{dt}}
Jerk=dtda
J e r k Jerk Jerk的绝对值越小, a a a的变化越平缓,意味着越舒适。
find f ( t ) f(t) f(t) 使得 ∫ 0 T ( d 3 f d t 3 ) 2 d t {\normalsize \int_{0}^{T} (\frac{d^3f}{dt^3})^2dt} ∫0T(dt3d3f)2dt最小
subject to :
S ( 0 ) = S 0 , S ( T ) = S n S ˙ ( 0 ) = v 0 , S ˙ ( T ) = v n S ¨ ( 0 ) = a 0 , S ¨ ( T ) = a n S(0)=S_{0},S(T)=S_{n}\\ \dot S(0)=v_{0},\dot S(T)=v_{n}\\ \ddot S(0)=a_{0},\ddot S(T)=a_{n} S(0)=S0,S(T)=SnS˙(0)=v0,S˙(T)=vnS¨(0)=a0,S¨(T)=an
显然
f
(
t
)
f(t)
f(t)只可能是在
[
0
,
T
]
[0,T]
[0,T]上是有界连续函数,因为无论是无界函数,还是有界间断函数都会使
J
e
r
k
Jerk
Jerk出现无穷大
f
(
t
)
f(t)
f(t):五次多项式
化简约束:
S
(
T
)
−
S
(
0
)
=
∫
0
T
f
˙
d
t
=
C
0
S
˙
(
T
)
−
S
˙
(
0
)
=
∫
0
T
f
¨
d
t
=
C
1
S
¨
(
T
)
−
S
¨
(
0
)
=
∫
0
T
f
(
3
)
d
t
=
C
2
S(T)-S(0)=\int_{0}^{T} \dot fdt=C_{0}\\ \dot S(T)-\dot S(0)=\int_{0}^{T} \ddot fdt=C_{1}\\ \ddot S(T)-\ddot S(0)=\int_{0}^{T} {f}^{(3)} dt=C_{2}
S(T)−S(0)=∫0Tf˙dt=C0S˙(T)−S˙(0)=∫0Tf¨dt=C1S¨(T)−S¨(0)=∫0Tf(3)dt=C2
问题描述:
问题变为求
∫
0
T
f
(
3
)
d
t
\int_{0}^{T} {f}^{(3)} dt
∫0Tf(3)dt在约束
∫
0
T
(
f
˙
−
C
0
T
)
d
t
=
0
,
∫
0
T
(
f
¨
−
C
1
T
)
d
t
=
0
,
∫
0
T
(
f
(
3
)
−
C
2
T
)
d
t
=
0
\int_{0}^{T} (\dot f-\frac{C_{0}}{T})dt=0,\int_{0}^{T} (\ddot f-\frac{C_{1}}{T})dt=0,\int_{0}^{T} ({f}^{(3)}-\frac{C_{2}}{T})dt=0
∫0T(f˙−TC0)dt=0,∫0T(f¨−TC1)dt=0,∫0T(f(3)−TC2)dt=0下的极小值
拉格朗日法:
∫
0
T
f
(
3
)
d
t
+
λ
1
∫
0
T
(
f
˙
−
C
0
T
)
d
t
+
λ
2
∫
0
T
(
f
¨
−
C
1
T
)
d
t
+
λ
3
∫
0
T
(
f
(
3
)
−
C
2
T
)
d
t
=
∫
0
T
(
λ
1
f
˙
+
λ
2
f
¨
+
λ
3
f
(
3
)
+
f
(
3
)
2
−
λ
1
C
0
T
−
λ
2
C
1
T
−
λ
3
C
2
T
)
d
t
=
∫
0
T
L
d
t
\int_{0}^{T} {f}^{(3)}dt+ \lambda _{1}\int_{0}^{T} (\dot f-\frac{C_{0}}{T})dt+\lambda _{2}\int_{0}^{T} (\ddot f-\frac{C_{1}}{T})dt+\lambda _{3}\int_{0}^{T} ({f}^{(3)}-\frac{C_{2}}{T})dt\\ =\ \int_{0}^{T} (\lambda _{1}\dot f +\lambda _{2}\ddot f+\lambda _{3}{f}^{(3)} +{{f}^{(3)}}^2- \lambda _{1}\frac{C_{0}}{T} -\lambda _{2}\frac{C_{1}}{T}-\lambda _{3}\frac{C_{2}}{T})dt\ =\int_{0}^{T} Ldt
∫0Tf(3)dt+λ1∫0T(f˙−TC0)dt+λ2∫0T(f¨−TC1)dt+λ3∫0T(f(3)−TC2)dt= ∫0T(λ1f˙+λ2f¨+λ3f(3)+f(3)2−λ1TC0−λ2TC1−λ3TC2)dt =∫0TLdt
用到广义
E
u
l
e
r
−
L
a
g
r
a
r
g
e
Euler-Lagrarge
Euler−Lagrarge方程
∂
L
∂
f
−
d
d
t
(
∂
L
∂
f
˙
)
+
d
2
d
t
2
(
∂
L
∂
f
¨
)
−
d
3
d
t
3
(
∂
L
∂
f
(
3
)
)
=
0
\frac{\partial L}{\partial f} -\frac{d}{dt} (\frac{\partial L}{\partial \dot f} )+\frac{d^2}{dt^2} (\frac{\partial L}{\partial \ddot f})-\frac{d^3}{dt^3} (\frac{\partial L}{\partial {f}^{(3)}})=0
∂f∂L−dtd(∂f˙∂L)+dt2d2(∂f¨∂L)−dt3d3(∂f(3)∂L)=0
将
∂
L
∂
f
=
0
,
∂
L
∂
f
˙
=
λ
1
,
∂
L
∂
f
¨
=
λ
2
,
∂
L
∂
f
(
3
)
=
λ
3
+
2
f
(
3
)
\frac{\partial L}{\partial f} =0,\frac{\partial L}{\partial \dot f} =\lambda _{1},\frac{\partial L}{\partial \ddot f} =\lambda _{2},\frac{\partial L}{\partial {f}^{(3)} } =\lambda _{3}+2{f}^{(3)}
∂f∂L=0,∂f˙∂L=λ1,∂f¨∂L=λ2,∂f(3)∂L=λ3+2f(3)代入广义
E
u
l
e
r
−
L
a
g
r
a
r
g
e
Euler-Lagrarge
Euler−Lagrarge方程得:
d
3
d
t
3
(
λ
3
+
2
f
(
3
)
)
=
0
\frac{d^3}{dt^3}(\lambda _{3}+2{f}^{(3)})=0
dt3d3(λ3+2f(3))=0
推导过程:
f
(
6
)
(
t
)
=
0
f
(
5
)
(
t
)
=
a
0
f
(
4
)
(
t
)
=
a
0
t
+
a
1
f
(
3
)
(
t
)
=
1
2
a
0
t
2
+
a
1
t
+
a
2
f
(
2
)
(
t
)
=
1
6
a
0
t
3
+
1
2
a
1
t
2
+
a
2
t
+
a
3
f
(
1
)
(
t
)
=
1
24
a
0
t
4
+
1
6
a
1
t
3
+
1
2
a
2
t
+
a
3
t
+
a
4
f
(
t
)
=
1
120
a
0
t
5
+
1
24
a
1
t
4
+
1
6
a
2
t
3
+
1
2
a
3
t
2
+
a
4
t
+
a
5
\begin{array}{l} f^{(6)}(t)=0 \\ f^{(5)}(t)=a_{0} \\ f^{(4)}(t)=a_{0} t+a_{1} \\ f^{(3)}(t)=\frac{1}{2} a_{0} t^{2}+a_{1} t+a_{2} \\ f^{(2)}(t)=\frac{1}{6} a_{0} t^{3}+\frac{1}{2} a_{1} t^{2}+a_{2} t+a_{3} \\ f^{(1)}(t)=\frac{1}{24} a_{0} t^{4}+\frac{1}{6} a_{1} t^{3}+\frac{1}{2} a_{2} t+a_{3} t+a_{4} \\ \\ \LARGE f(t)=\frac{1}{120} a_{0} t^{5}+\frac{1}{24} a_{1} t^{4}+\frac{1}{6} a_{2} t^3+\frac{1}{2} a_{3} t^2+a_{4} t+a_{5} \end{array}
f(6)(t)=0f(5)(t)=a0f(4)(t)=a0t+a1f(3)(t)=21a0t2+a1t+a2f(2)(t)=61a0t3+21a1t2+a2t+a3f(1)(t)=241a0t4+61a1t3+21a2t+a3t+a4f(t)=1201a0t5+241a1t4+61a2t3+21a3t2+a4t+a5
2.2 凸优化和非凸优化
① 自动驾驶规划目标:算出一条满足约束的最优轨迹
衡量轨迹质量往往用cost function表示,代价函数越小,意味着越平滑,越舒适,当然也要满足各种约束。
指标:平滑、舒适、尽可能短
约束:轨迹连续、无碰撞、交规、车辆动力学
② 凸优化性质
(a) 代价函数只有一个极小值点且为最小值(凸函数)
(b) 约束空间是一块完整的、不破碎的空间(凸空间)
凸优化:求凸函数在凸空间的最小值问题
③ 自动驾驶避障约束空间是非凸的
(a) 静态和动态避障约束空间都不是凸空间
静态避障:
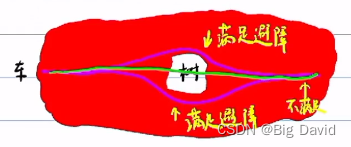
动态避障:
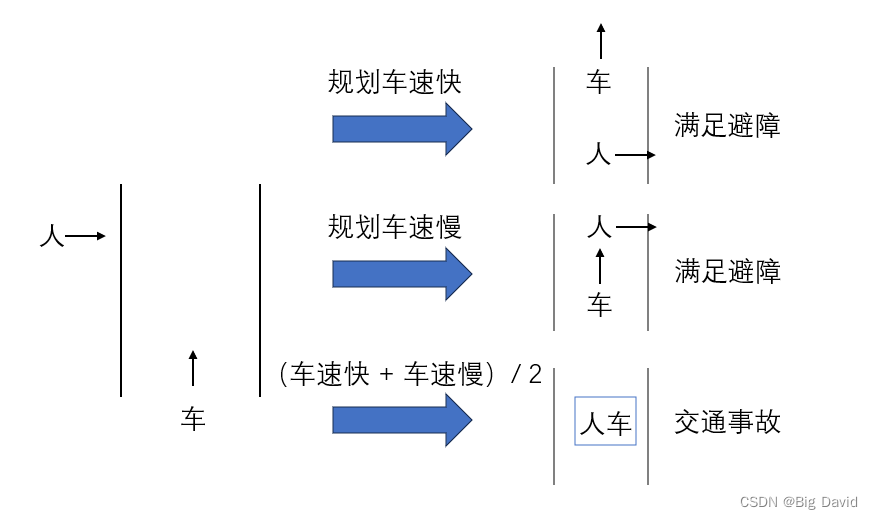
(b) 求解非凸问题的主要思路是找非凸问题中的凸结构
非凸空间 => 离散化 => 粗解(base) => 迭代 => 最终解
启发式算法:
先随机在约束空间采样一些离散的函数值比大小,取最小的作为迭代初值。
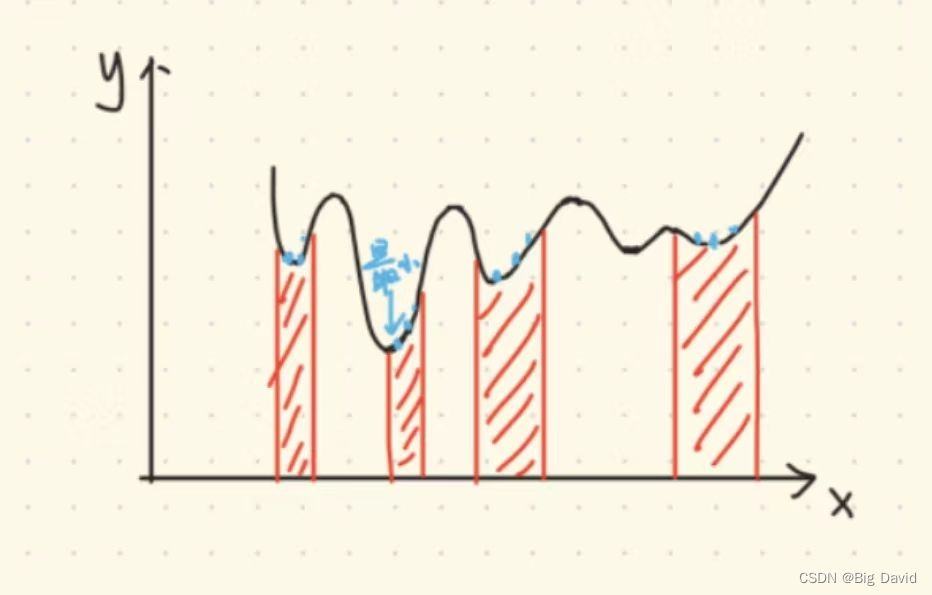
2.3 直角坐标与自然坐标转换
龙格现象:高次多项式拟合可能会出现震荡,慎用高次多项式。

以Cartesian坐标为准
r n ⃗ \vec{r_n} rn:车的位矢
v ⃗ \vec{v} v:车的速度
a ⃗ \vec{a} a:车的加速度
k h k_h kh:车的位矢在车的轨迹上的曲率
τ h ⃗ \vec{\tau _h} τh:车的位矢在车的轨迹上的切线方向单位向量
n h ⃗ \vec{ n_h} nh:车的位矢在车的轨迹上的法线方向单位向量
r r ⃗ \vec{r_r} rr:投影位矢
S ˙ \dot S S˙:投影速率
k r k_r kr:投影位矢在道路几何上的曲率
τ r ⃗ \vec{\tau _r} τr:投影位矢在道路几何上的切线方向单位向量
n r ⃗ \vec{n _r} nr:投影位矢在道路几何上的法线方向单位向量
已知
r
⃗
h
,
v
⃗
h
,
a
⃗
h
,
k
h
,
τ
⃗
h
,
n
⃗
h
\vec{r}_{h}, \vec{v}_{h}, \vec{a}_{h}, k_{h}, \vec{\tau}_{h}, \vec{n}_{h}
rh,vh,ah,kh,τh,nh
己知 frenet 坐标系起点
(
x
0
,
y
0
)
\left(x_{0}, y_{0}\right)
(x0,y0)
求
s
,
s
˙
,
s
¨
,
l
,
l
′
,
l
′
′
s
˙
=
d
s
d
t
l
′
=
d
l
d
s
s, \dot{s}, \ddot{s}, l, l^{\prime}, l^{\prime \prime} \quad \dot{s}=\frac{d s}{d t} \quad l^{\prime}=\frac{d l}{d s} \quad
s,s˙,s¨,l,l′,l′′s˙=dtdsl′=dsdl
d
s
ds
ds 为frenet坐标轴的弧长
主要思路:
(1)找车在Frenet坐标系下的投影点在笛卡尔坐标下的坐标,记为
(
x
r
,
y
r
,
k
r
,
θ
r
)
(x_r,y_r,k_r,\theta_r)
(xr,yr,kr,θr)
(2)利用向量三角形,以及微积分求
s
,
s
˙
,
s
¨
,
l
,
l
′
,
l
′
s,\dot s,\ddot s,l,l_{}',l_{}'
s,s˙,s¨,l,l′,l′
核心公式:
r
⃗
r
+
l
n
⃗
r
=
r
⃗
h
\vec r_r+l\vec n_r=\vec r_h
rr+lnr=rh
7个辅助公式:
r
˙
→
h
=
v
⃗
=
∣
v
⃗
∣
τ
⃗
h
r
˙
⃗
r
=
s
˙
τ
⃗
r
τ
⃗
h
=
k
h
∣
v
⃗
∣
n
⃗
h
n
⃗
h
=
−
k
h
∣
v
⃗
∣
τ
⃗
h
τ
˙
⃗
r
=
k
r
s
˙
n
⃗
r
n
˙
→
r
=
−
k
r
s
˙
τ
⃗
r
a
⃗
=
∣
v
˙
⃗
∣
τ
⃗
h
+
∣
v
⃗
∣
2
k
h
n
⃗
h
\begin{array}{l} \overrightarrow{\dot{r}}_{h}=\vec{v}=|\vec{v}| \vec{\tau}_{h} \\ \vec{\dot r}_{r}=\dot{s} \vec{\tau}_{r} \\ \vec{\tau}_{h}=k_{h}|\vec{v}| \vec{n}_{h} \\ \vec{n}_{h}=-k_{h}|\vec{v}| \vec{\tau}_{h} \\ \vec{\dot \tau}_{r}=k_{r} \dot{s} \vec{n}_{r} \\ \overrightarrow{\dot{n}}_{r}=-k_{r} \dot{s} \vec{\tau}_{r} \\ \vec{a}=|\vec{\dot v}| \vec{\tau}_{h}+|\vec{v}|^{2} k_{h} \vec{n}_{h} \end{array}
r˙h=v=∣v∣τhr˙r=s˙τrτh=kh∣v∣nhnh=−kh∣v∣τhτ˙r=krs˙nrn˙r=−krs˙τra=∣v˙∣τh+∣v∣2khnh
向量法详细推导见博客
s
,
s
˙
,
s
¨
,
l
,
l
˙
,
l
¨
,
l
′
,
l
′
′
s,\dot s,\ddot s,l,\dot l,\ddot l,l_{}',l_{}''
s,s˙,s¨,l,l˙,l¨,l′,l′′八个变量,独立的只有6个,因为
l
˙
,
l
¨
\dot l,\ddot l
l˙,l¨可以由
l
′
,
l
′
′
l_{}',l_{}''
l′,l′′推导过来
l
˙
=
l
′
∗
s
˙
l
¨
=
d
l
d
t
=
d
(
l
′
s
˙
)
d
t
=
d
l
′
d
t
s
˙
+
l
′
⋅
s
¨
=
d
l
′
d
s
⋅
d
s
d
t
⋅
s
˙
+
l
′
s
¨
=
l
′
′
s
˙
2
+
l
′
s
¨
\dot l= l'*\dot s\\ \\ \begin{aligned} \ddot{l}=\frac{d l}{d t}=\frac{d\left(l^{\prime} \dot{s}\right)}{d t} & =\frac{d l^{\prime}}{d t} \dot{s}+l^{\prime} \cdot \ddot{s} \\ & =\frac{d l^{\prime}}{d s} \cdot \frac{d s}{d t} \cdot \dot{s}+l^{\prime} \ddot{s} \\ & =l^{\prime \prime} \dot{s}^{2}+l^{\prime} \ddot{s} \end{aligned}
l˙=l′∗s˙l¨=dtdl=dtd(l′s˙)=dtdl′s˙+l′⋅s¨=dsdl′⋅dtds⋅s˙+l′s¨=l′′s˙2+l′s¨
EM planner:
s
,
s
˙
,
s
¨
,
l
,
l
′
,
l
′
s,\dot s,\ddot s,l,l_{}',l_{}'
s,s˙,s¨,l,l′,l′
Lattice planner:
s
,
s
˙
,
s
¨
,
l
,
l
˙
,
l
¨
s,\dot s,\ddot s,l,\dot l,\ddot l
s,s˙,s¨,l,l˙,l¨
s的计算方法:
主要思路:
用直线长度代替弧长,当路径点足够密集,误差可以忽略

这里直接给出Frenet和Cartesian互转的公式:

百度Apollo Frenet和Cartesian互转的代码:
modules/common/math/cartesian_frenet_conversion.h
static void cartesian_to_frenet(const double rs, const double rx,
const double ry, const double rtheta,
const double rkappa, const double rdkappa,
const double x, const double y,
const double v, const double a,
const double theta, const double kappa,
std::array<double, 3>* const ptr_s_condition,
std::array<double, 3>* const ptr_d_condition);
static void frenet_to_cartesian(const double rs, const double rx,
const double ry, const double rtheta,
const double rkappa, const double rdkappa,
const std::array<double, 3>& s_condition,
const std::array<double, 3>& d_condition,
double* const ptr_x, double* const ptr_y,
double* const ptr_theta,
double* const ptr_kappa, double* const ptr_v,
double* const ptr_a);
modules/common/math/cartesian_frenet_conversion.cpp
void CartesianFrenetConverter::cartesian_to_frenet(
const double rs, const double rx, const double ry, const double rtheta,
const double rkappa, const double rdkappa, const double x, const double y,
const double v, const double a, const double theta, const double kappa,
std::array<double, 3>* const ptr_s_condition,
std::array<double, 3>* const ptr_d_condition) {
const double dx = x - rx;
const double dy = y - ry;
const double cos_theta_r = std::cos(rtheta);
const double sin_theta_r = std::sin(rtheta);
const double cross_rd_nd = cos_theta_r * dy - sin_theta_r * dx;
ptr_d_condition->at(0) =
std::copysign(std::sqrt(dx * dx + dy * dy), cross_rd_nd);
const double delta_theta = theta - rtheta;
const double tan_delta_theta = std::tan(delta_theta);
const double cos_delta_theta = std::cos(delta_theta);
const double one_minus_kappa_r_d = 1 - rkappa * ptr_d_condition->at(0);
ptr_d_condition->at(1) = one_minus_kappa_r_d * tan_delta_theta;
const double kappa_r_d_prime =
rdkappa * ptr_d_condition->at(0) + rkappa * ptr_d_condition->at(1);
ptr_d_condition->at(2) =
-kappa_r_d_prime * tan_delta_theta +
one_minus_kappa_r_d / cos_delta_theta / cos_delta_theta *
(kappa * one_minus_kappa_r_d / cos_delta_theta - rkappa);
ptr_s_condition->at(0) = rs;
ptr_s_condition->at(1) = v * cos_delta_theta / one_minus_kappa_r_d;
const double delta_theta_prime =
one_minus_kappa_r_d / cos_delta_theta * kappa - rkappa;
ptr_s_condition->at(2) =
(a * cos_delta_theta -
ptr_s_condition->at(1) * ptr_s_condition->at(1) *
(ptr_d_condition->at(1) * delta_theta_prime - kappa_r_d_prime)) /
one_minus_kappa_r_d;
}
void CartesianFrenetConverter::frenet_to_cartesian(
const double rs, const double rx, const double ry, const double rtheta,
const double rkappa, const double rdkappa,
const std::array<double, 3>& s_condition,
const std::array<double, 3>& d_condition, double* const ptr_x,
double* const ptr_y, double* const ptr_theta, double* const ptr_kappa,
double* const ptr_v, double* const ptr_a) {
ACHECK(std::abs(rs - s_condition[0]) < 1.0e-6)
<< "The reference point s and s_condition[0] don't match";
const double cos_theta_r = std::cos(rtheta);
const double sin_theta_r = std::sin(rtheta);
*ptr_x = rx - sin_theta_r * d_condition[0];
*ptr_y = ry + cos_theta_r * d_condition[0];
const double one_minus_kappa_r_d = 1 - rkappa * d_condition[0];
const double tan_delta_theta = d_condition[1] / one_minus_kappa_r_d;
const double delta_theta = std::atan2(d_condition[1], one_minus_kappa_r_d);
const double cos_delta_theta = std::cos(delta_theta);
*ptr_theta = NormalizeAngle(delta_theta + rtheta);
const double kappa_r_d_prime =
rdkappa * d_condition[0] + rkappa * d_condition[1];
*ptr_kappa = (((d_condition[2] + kappa_r_d_prime * tan_delta_theta) *
cos_delta_theta * cos_delta_theta) /
(one_minus_kappa_r_d) +
rkappa) *
cos_delta_theta / (one_minus_kappa_r_d);
const double d_dot = d_condition[1] * s_condition[1];
*ptr_v = std::sqrt(one_minus_kappa_r_d * one_minus_kappa_r_d *
s_condition[1] * s_condition[1] +
d_dot * d_dot);
const double delta_theta_prime =
one_minus_kappa_r_d / cos_delta_theta * (*ptr_kappa) - rkappa;
*ptr_a = s_condition[2] * one_minus_kappa_r_d / cos_delta_theta +
s_condition[1] * s_condition[1] / cos_delta_theta *
(d_condition[1] * delta_theta_prime - kappa_r_d_prime);
}
3 参考线reference_line
3.0 前言
决策规划流程:
① 全局规划生成一条参考线
② 静态障碍物投影到以参考线为坐标轴的Frenet坐标系上
③ 决策算法对障碍物做决策(往左绕,往右绕,忽略)开辟最优凸空间
④ 规划算法在凸空间搜素出最优的路径
⑤ 后处理,在规划轨迹中选一个点,坐标转成Cartesian,输出给控制跟踪
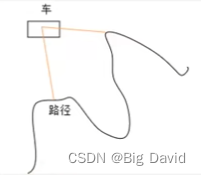
需要参考线的原因:
(1)参考线是解决方案,能够解决导航路径过长,不平滑的问题
(2)过长的路径不利于坐标转换(找匹配点,计算s的长度)
(3)过长的路径,障碍物投影可能不唯一
(4)路径不平滑
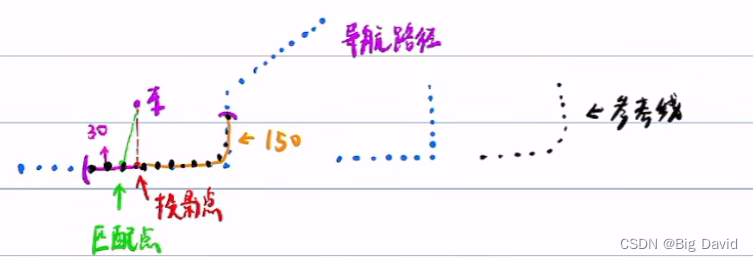
在每个规划周期内,找到车在导航路径上的投影点,以投影点为坐标原点,往后取30m,往前取150m范围内的点,做平滑,平滑后的点的集合称为参考线。
3.1 参考线平滑算法
参考线的三个代价函数:
(1)平滑代价

∣
P
1
P
3
⃗
∣
|\vec {P_1P_3}|
∣P1P3∣衡量平滑与不平滑的标准。
∣
P
1
P
3
⃗
∣
|\vec {P_1P_3}|
∣P1P3∣越小,越平滑。
(2)紧凑型代价
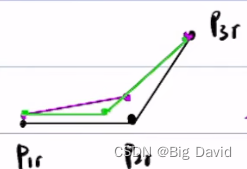
长度尽可能均匀、紧凑

(3)相似代价
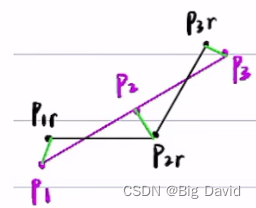
∣
P
1
P
1
r
⃗
∣
+
∣
P
2
P
2
r
⃗
∣
+
∣
P
3
P
3
r
⃗
∣
|\vec {P_1P_{1r}}|+|\vec {P_2P_{2r}}|+|\vec {P_3P_{3r}}|
∣P1P1r∣+∣P2P2r∣+∣P3P3r∣越小,越接近原路径几何。
总结:
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x1,x2,x3为优化后的路径点。希望cost function越小越好

本质是二次规划问题
1
2
X
T
H
X
+
f
T
X
=
X
T
(
H
2
)
X
+
f
T
X
\begin{array}{l} \frac{1}{2} X^{T} H X+f^{T} X=X^{T} (\frac{H}{2} )X+f^{T} X \end{array}
21XTHX+fTX=XT(2H)X+fTX
令 H = 2 ( w smooth A 1 T A 1 + w length A 2 T A 2 + w ref A 3 T A 3 ) , f T = w ref h T H=2\left(w_{\text {smooth }} A_{1}^{T} A_{1}+w_{\text {length }} A_{2}^{T} A_{2}+w_{\text {ref }} A_{3}^{T} A_{3}\right), f^{T}=w_{\text {ref }} h^{T} H=2(wsmooth A1TA1+wlength A2TA2+wref A3TA3),fT=wref hT
约束:
x
=
(
x
1
,
y
1
,
.
.
.
,
x
n
,
y
n
)
x = (x_1,y_1,...,x_n,y_n)
x=(x1,y1,...,xn,yn)
x
r
e
f
=
(
x
1
r
,
y
1
r
,
.
.
.
,
x
n
r
,
y
n
r
)
x_{ref}=(x_{1r},y_{1r},...,x_{nr},y_{nr})
xref=(x1r,y1r,...,xnr,ynr)
x
x
x与
x
r
e
f
x_{ref}
xref不要太远
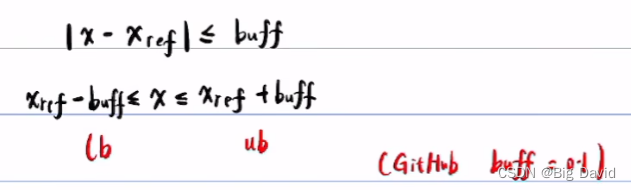
曲率约束:非线性约束(一般与车的最大侧向加速度有关)
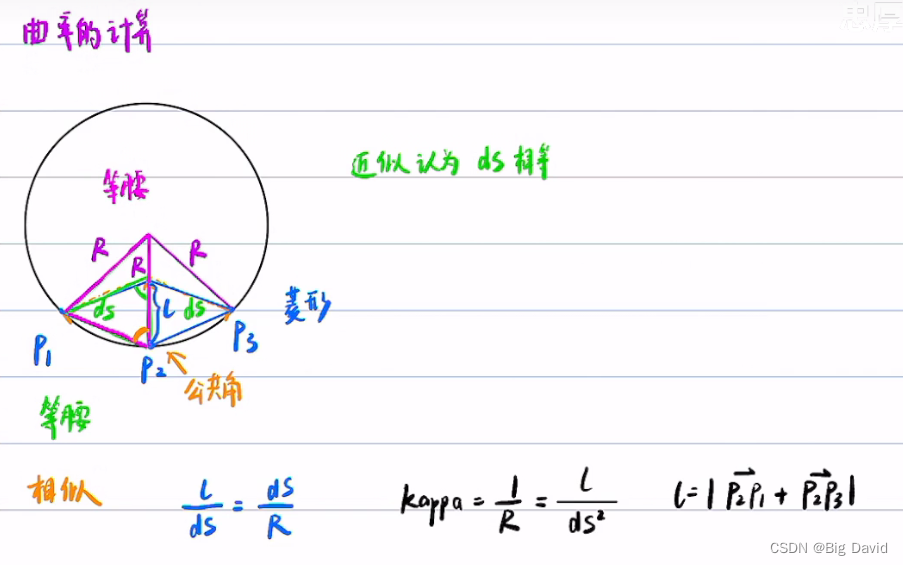
3.2 Fem smooth平滑
在Apollo中叫 Fem smoother
优势:优化变量少
缺点:无法保证曲率是连续的,添加曲率约束求解麻烦
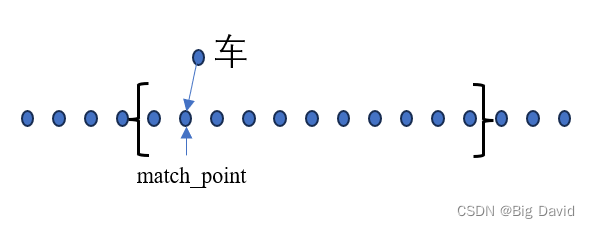
主要步骤:
(1)找匹配点
(2)采样(前150m,后30m)
(3)Fem smooth 平滑
目标:快,节省计算量(参考线是决策规划的基础和前提,因此必须要快)
怎么快?
(1)减少规划频率,规划算法会100ms执行一次,控制算法每10ms执行一次
(2)充分利用上一个规划周期的结果
一般做法:每个周期做遍历,但是这样速度慢,导航路径可能很长,遍历很费时
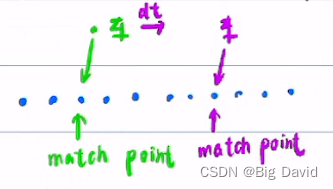
改进:
如何充分利用上一个规划周期的结果
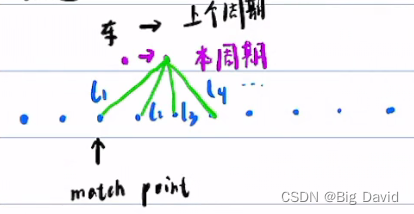
以上个周期的match point为起点做遍历,一旦有
l
i
+
1
>
l
i
l_{i+1}>l_{i}
li+1>li,立即退出遍历。
l
i
l_i
li对应的点作为本周期的匹配点。
判断遍历的方向:
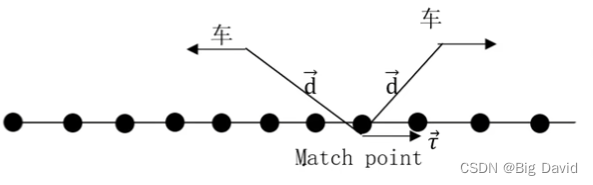
a
)
向前遍历:
d
→
⋅
τ
⃗
>
0
b
)
向后遍历:
d
→
⋅
τ
⃗
<
0
c
)
本周期的匹配点
=
上周期的匹配点:
∣
d
→
⋅
τ
⃗
∣
<
1
e
−
3
a) 向前遍历: \overrightarrow{\mathrm{d}} \cdot \vec{\tau}>0 \\ b) 向后遍历: \overrightarrow{\mathrm{d}} \cdot \vec{\tau}<0 \\ c)本周期的匹配点=上周期的匹配点: |\overrightarrow{\mathrm{d}} \cdot \vec{\tau}|<1e-3
a)向前遍历:d⋅τ>0b)向后遍历:d⋅τ<0c)本周期的匹配点=上周期的匹配点:∣d⋅τ∣<1e−3
本方法可以大大加速找匹配点
带来的问题:只适用于上个匹配点结果附近只有一个极小值点
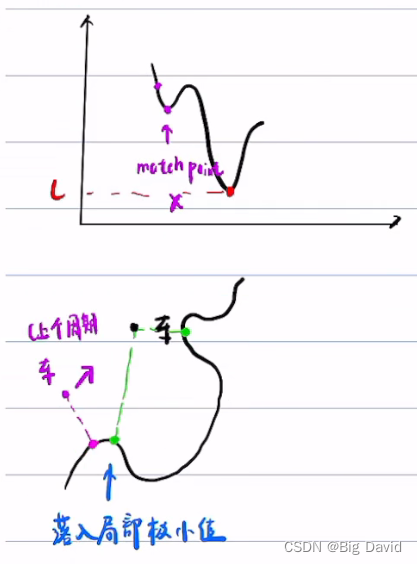
一般情况不会有这种问题,规划周期100ms,即使车速50m/s,车也只走了五米。五米的道路不会像上图一样扭曲的道路几何,在上一个规划周期的匹配点一般只有一个极小值。
改进:
增加increase变量记录l连续增加的次数


在Github算法里
(1)遍历
第一次运行遍历

不是第一次运行

(2)点不够的情况

(3)参考线拼接
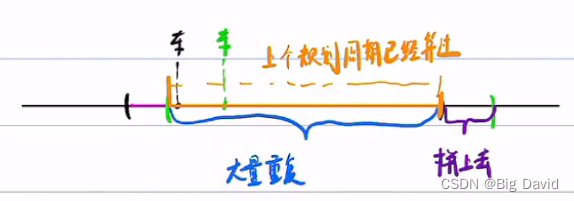
如何拼接:
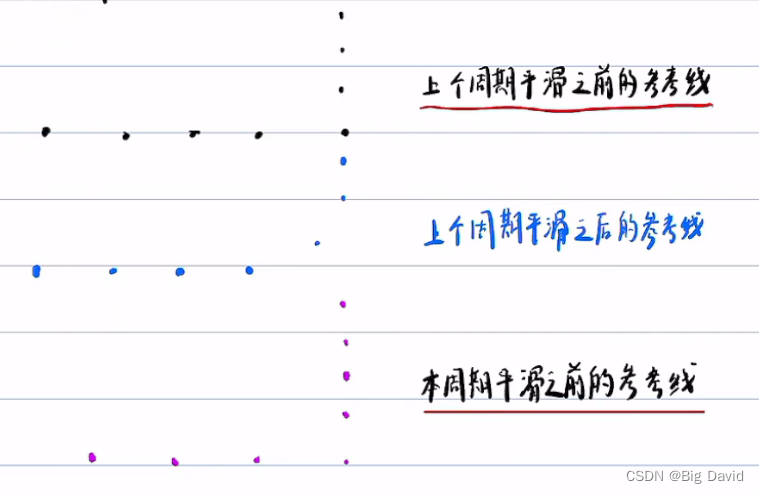
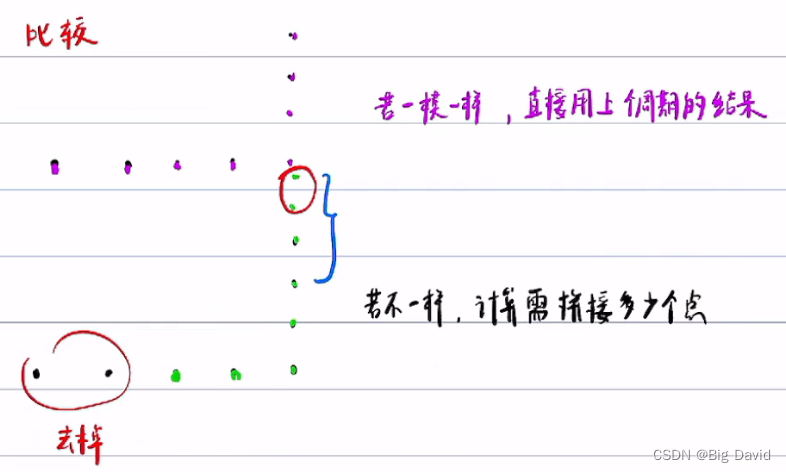
注意:
Fem smoother至少需要3个点
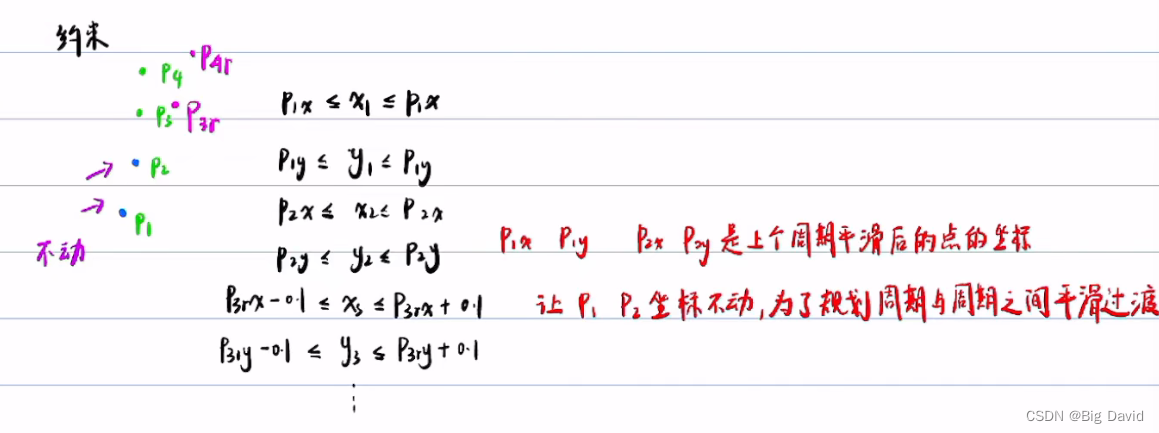
3.3 避障
3.3.1 规划起点

确定规划起点:
错误做法:定位得到的host_x,host_y投影到referenceline,得到SL坐标(0,
l
0
l_0
l0),以此点为路径规划的起点
正确做法:判断当前定位和上一个周期规划的结果是否误差太大
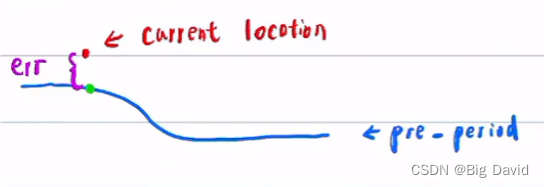


以(
s
0
,
l
0
s_0,l_0
s0,l0)作为规划的起点
为什么不能从定位的点作为规划起点:考虑到控制不完美,导致帧与帧之间的曲线是跳变的。
判断定位与轨迹的误差不太大的话,用上个轨迹的T+100ms的点作为本周期的规划起点,若误差较大,用车辆运动学进行外推
3.3.2 轨迹拼接
结合上一节,本人觉得理解老王对于规划起点的描述有点模糊,故拜读了下面这篇大佬写的博客,对于轨迹拼接思路一下子就通了。
参考博客:百度Apollo规划算法——轨迹拼接
在apollo的规划算法中,在每一帧规划开始时会调用一个轨迹拼接函数,返回一段拼接轨迹点集,并告诉我们是否重规划以及重规划的原因。
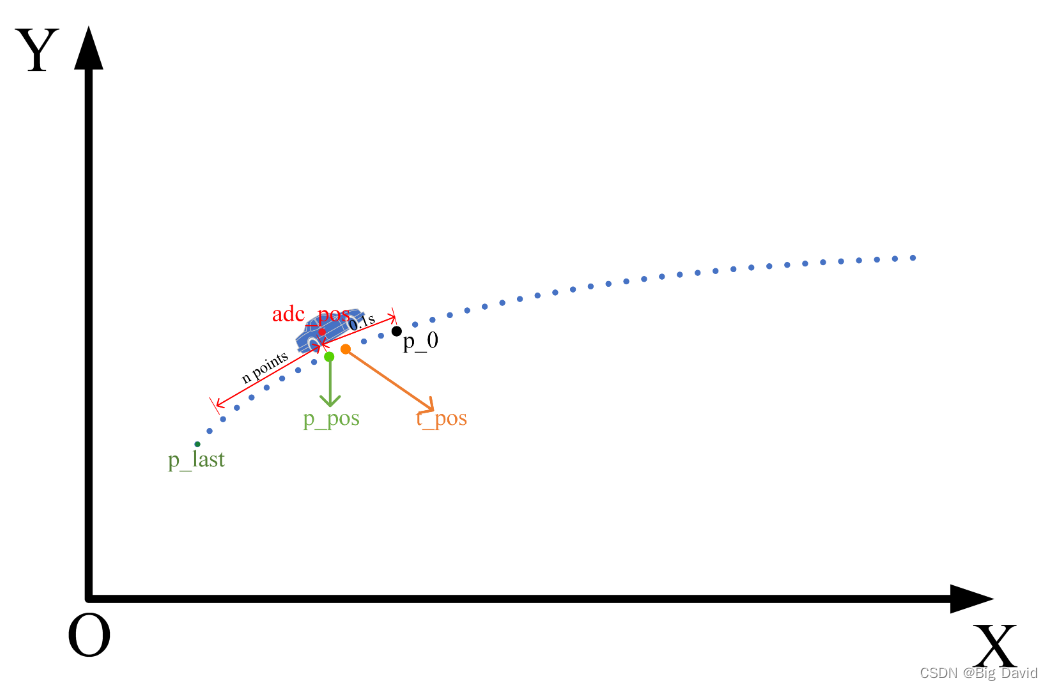
轨迹拼接:在每一帧轨迹规划的开始,我们需要确定规划的起始点 p 0 = ( x , y , v , a , θ , k , t ) p_0=(x,y,v,a,\theta,k,t) p0=(x,y,v,a,θ,k,t),起始点给定了规划的初始状态,然后结合当前帧的环境信息并调用规划算法规划生成当前帧轨迹。
方案1
根据ADC(Autonomous Driving Car)实际位置状态信息,通过车辆运动学推导100ms后的位置状态信息,作为规划起始点状态,在Apollo中,这一方案叫做重规划Replan。
方案2:考虑的是连续帧之间轨迹的平滑性和连续性
根据当前帧时间戳以及ADC实际位置信息,在上一帧轨迹中寻找匹配点,将上一帧轨迹中匹配点往后100ms所对应的轨迹点作为当前帧的规划起始状态点,待当前帧规划生成轨迹后,再和上一帧轨迹中所选择的规划起始点前一段距离的轨迹点进行拼接,形成一条完整的车辆运动轨迹(思路一下就清晰了,牛逼!),发送给下游控制模块。
理论上,如果控制跟踪和定位完美,不会出现任何误差,则完全可以使用方案1选择规划起始点,但是,由于定位误差和控制误差/滞后的原因,会导致每一规划时刻ADC位置大概率的偏离上一帧所规划的轨迹点,如果此时仍采用方案1,会导致当前帧所规划轨迹和上一帧规划轨迹的不平滑和不连续,从而导致控制的抖动,也可能会引起ADC行驶轨迹发散,跟踪误差越来越大,偏离设定参考线。而方案2可以保证ADC附近一段范围内前后两帧轨迹的平滑性,从而不断引导ADC沿着期望轨迹行驶。
3.3.3 结合Apollo代码理解轨迹拼接的细节
选择方案1的情况:
- 上一帧不存在轨迹(一般是起步或上一帧规划失败的情况)
- 没有使能方案2进行轨迹拼接
- 没有处在自动驾驶模式
- 上一帧存在轨迹但是没有轨迹点
- 当前时间相对于上一帧的相对时间戳小于上一帧起点相对时间戳
- 时间匹配点超出上一帧轨迹点的终点实际范围
- 匹配点处不存在匹配的path_point
- ADC实际位置和匹配点横纵向偏差超过给定阈值
方案1生成轨迹拼接点主要有两种情况:
① 起步阶段:由于起步阶段属于规划算法执行的第一帧,且速度、加速度值很小,可以直接使用当前状态点作为规划的起始状态点
② 非起步阶段:则根据当前ADC状态点结合运动学模型外推T时间之后的状态点作为本帧规划起始点
[ x t + 1 y t + 1 ψ t + 1 ] = [ x t y t ψ t ] + [ cos ( ψ ) sin ( ψ ) tan ( δ f ) l ] ⋅ v \left[\begin{array}{l} x_{t+1} \\ y_{t+1} \\ \psi_{t+1} \end{array}\right]=\left[\begin{array}{l} x_{t} \\ y_{t} \\ \psi_{t} \end{array}\right]+\left[\begin{array}{c} \cos (\psi) \\ \sin (\psi) \\ \frac{\tan \left(\delta_{f}\right)}{l} \end{array}\right] \cdot v xt+1yt+1ψt+1 = xtytψt + cos(ψ)sin(ψ)ltan(δf) ⋅v
方案二(以上情况均不满足时):
该方案同时考虑了时间匹配和位置匹配
时间匹配:根据当前时间戳和上一帧轨迹起点的时间戳对比,计算当前时间ADC应该到达的时间匹配点(图中t_pos)及该匹配点在上一帧轨迹中对应的索引值t_index,若t_pos不存在路径点,则选择方案1。
位置匹配:根据ADC当前位置点在上一帧轨迹中寻找最近的匹配点(图中p_pos)及该匹配点在上一帧轨迹中对应的索引值p_index,并比较实际位置点和匹配点之间的横纵向位置偏差,若任一偏差超过给定阈值,则选择方案1。
若以上判断均通过,根据 (当前时刻的绝对时间 - 上一时刻轨迹的初始时间 + planning_cycle_time) 得到forward_rel_time,选取时间匹配索引和位置匹配索引中的较小索引作为匹配点索引值matched_index,在上一帧的轨迹上截取出matched_index往前n个点开始,至forward_rel_time的一段轨迹,作为stitching_trajectory。最后,遍历这段轨迹,对其relative_time和s进行赋值。最终,使用stitching_trajectory的最后一个点,即图中的 p 0 p_0 p0,作为当前帧轨迹规划的起始点。
选择当前时间+planning_cycle_time的时间对应的上一帧轨迹的位置点作为本帧规划起点的原因:当本帧规划需要时间planning_cycle_time,将生成轨迹送到规划模块时对应的实际时间理论上就是当前时间+planning_cycle_time。
TrajectoryStitcher::ComputeStitchingTrajectory
/* Planning from current vehicle state if:
1. the auto-driving mode is off
(or) 2. we don't have the trajectory from last planning cycle
(or) 3. the position deviation from actual and target is too high
*/
std::vector<TrajectoryPoint> TrajectoryStitcher::ComputeStitchingTrajectory(
const VehicleState& vehicle_state, const double current_timestamp,
const double planning_cycle_time, const size_t preserved_points_num,
const bool replan_by_offset, const PublishableTrajectory* prev_trajectory,
std::string* replan_reason) {
//a.是否使能轨迹拼接
if (!FLAGS_enable_trajectory_stitcher) {
*replan_reason = "stitch is disabled by gflag.";
return ComputeReinitStitchingTrajectory(planning_cycle_time, vehicle_state);
}
//b.上一帧是否生成轨迹
if (!prev_trajectory) {
*replan_reason = "replan for no previous trajectory.";
return ComputeReinitStitchingTrajectory(planning_cycle_time, vehicle_state);
}
//c.是否处于自动驾驶模式
if (vehicle_state.driving_mode() != canbus::Chassis::COMPLETE_AUTO_DRIVE) {
*replan_reason = "replan for manual mode.";
return ComputeReinitStitchingTrajectory(planning_cycle_time, vehicle_state);
}
//d.上一帧是否存在轨迹点
size_t prev_trajectory_size = prev_trajectory->NumOfPoints();
if (prev_trajectory_size == 0) {
*replan_reason = "replan for empty previous trajectory.";
return ComputeReinitStitchingTrajectory(planning_cycle_time, vehicle_state);
}
const double veh_rel_time = current_timestamp - prev_trajectory->header_time();
size_t time_matched_index = prev_trajectory->QueryLowerBoundPoint(veh_rel_time);
//e.判断当前时间相对于上一帧的相对时间戳是否小于上一帧起点相对时间戳
if (time_matched_index == 0 &&
veh_rel_time < prev_trajectory->StartPoint().relative_time()) {
*replan_reason =
"replan for current time smaller than the previous trajectory's first "
"time.";
return ComputeReinitStitchingTrajectory(planning_cycle_time, vehicle_state);
}
//f.判断时间匹配点是否超出上一帧轨迹点范围
if (time_matched_index + 1 >= prev_trajectory_size) {
*replan_reason =
"replan for current time beyond the previous trajectory's last time";
return ComputeReinitStitchingTrajectory(planning_cycle_time, vehicle_state);
}
auto time_matched_point = prev_trajectory->TrajectoryPointAt(
static_cast<uint32_t>(time_matched_index));
//g.判断时间匹配点处是否存在path_point
if (!time_matched_point.has_path_point()) {
*replan_reason = "replan for previous trajectory missed path point";
return ComputeReinitStitchingTrajectory(planning_cycle_time, vehicle_state);
}
size_t position_matched_index = prev_trajectory->QueryNearestPointWithBuffer(
{vehicle_state.x(), vehicle_state.y()}, 1.0e-6);
//计算实际位置点和匹配点的横纵向偏差
auto frenet_sd = ComputePositionProjection(
vehicle_state.x(), vehicle_state.y(),
prev_trajectory->TrajectoryPointAt(
static_cast<uint32_t>(position_matched_index)));
//h.判断横纵向偏差
if (replan_by_offset) {
auto lon_diff = time_matched_point.path_point().s() - frenet_sd.first;
auto lat_diff = frenet_sd.second;
//h.1:横向偏差不满足条件
if (std::fabs(lat_diff) > FLAGS_replan_lateral_distance_threshold) {
const std::string msg = absl::StrCat(
"the distance between matched point and actual position is too "
"large. Replan is triggered. lat_diff = ",
lat_diff);
*replan_reason = msg;
return ComputeReinitStitchingTrajectory(planning_cycle_time,
vehicle_state);
}
//h.2:纵向偏差不满足条件
if (std::fabs(lon_diff) > FLAGS_replan_longitudinal_distance_threshold) {
const std::string msg = absl::StrCat(
"the distance between matched point and actual position is too "
"large. Replan is triggered. lon_diff = ",
lon_diff);
*replan_reason = msg;
return ComputeReinitStitchingTrajectory(planning_cycle_time,
vehicle_state);
}
} else {
ADEBUG << "replan according to certain amount of lat and lon offset is "
"disabled";
}
//计算当前时刻后T时刻的时间,并计算其在上一帧轨迹中对应的索引值
double forward_rel_time = veh_rel_time + planning_cycle_time;
size_t forward_time_index =
prev_trajectory->QueryLowerBoundPoint(forward_rel_time);
ADEBUG << "Position matched index:\t" << position_matched_index;
ADEBUG << "Time matched index:\t" << time_matched_index;
//选择时间匹配索引和位置匹配索引中的较小索引作为匹配点索引
auto matched_index = std::min(time_matched_index, position_matched_index);
//构建拼接轨迹,<匹配索引点前n个点,当前时刻后的T时刻所对应的匹配点>
std::vector<TrajectoryPoint> stitching_trajectory(
prev_trajectory->begin() +
std::max(0, static_cast<int>(matched_index - preserved_points_num)),
prev_trajectory->begin() + forward_time_index + 1);
const double zero_s = stitching_trajectory.back().path_point().s();
for (auto& tp : stitching_trajectory) {
if (!tp.has_path_point()) {
*replan_reason = "replan for previous trajectory missed path point";
return ComputeReinitStitchingTrajectory(planning_cycle_time,
vehicle_state);
}
//适配时间和s值
tp.set_relative_time(tp.relative_time() + prev_trajectory->header_time() -
current_timestamp);
tp.mutable_path_point()->set_s(tp.path_point().s() - zero_s);
}
return stitching_trajectory;
}
3.4 避障
避障问题是非凸问题,存在多个极小值点,要怎样找到最终解?找粗解
3.4.1 避障流程
避障流程:
① 在离散空间上求最优路径,此最优路径开辟一个凸空间,在此凸空间上做二次规划,离散空间的最优路径称为粗解,粗解开辟凸空间,在这个凸空间上开辟最优解。
② 在离散空间上找到粗解:DP;在凸空间上优化最终解:QP
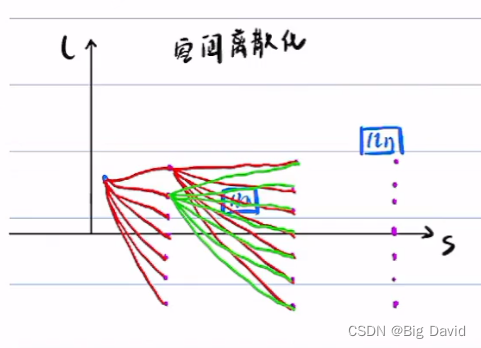
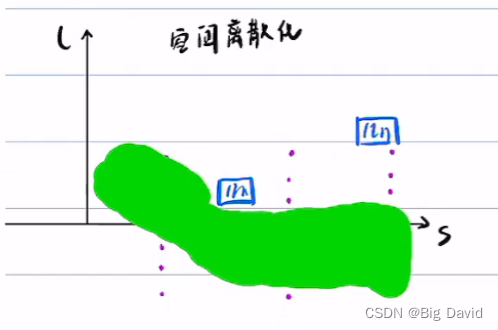
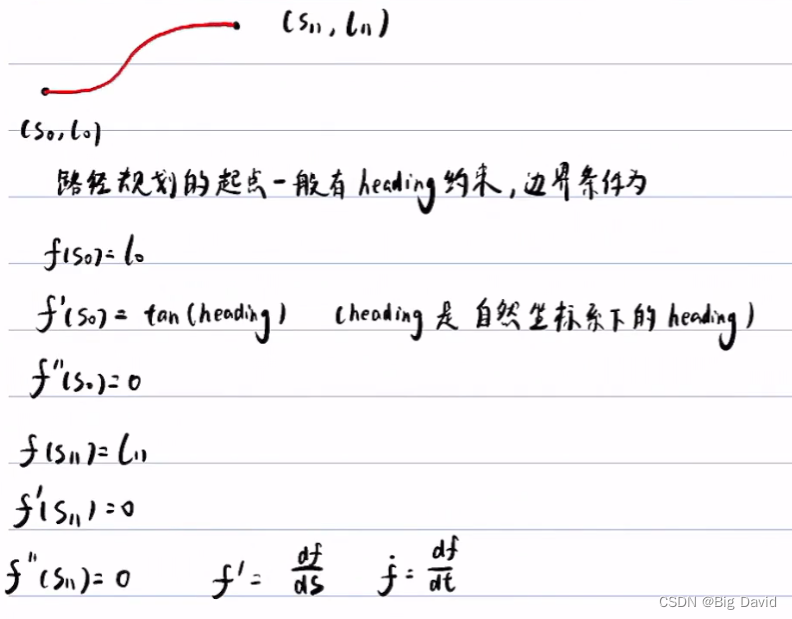
连接两点的曲线:五次多项式
l
=
f
(
s
)
=
a
0
+
a
1
s
+
a
2
s
2
+
.
.
.
+
a
5
s
5
l = f(s)=a_0+a_1s+a_2s^2+...+a_5s^5
l=f(s)=a0+a1s+a2s2+...+a5s5
3.4.2 代价函数
代价函数:评价路径的优劣
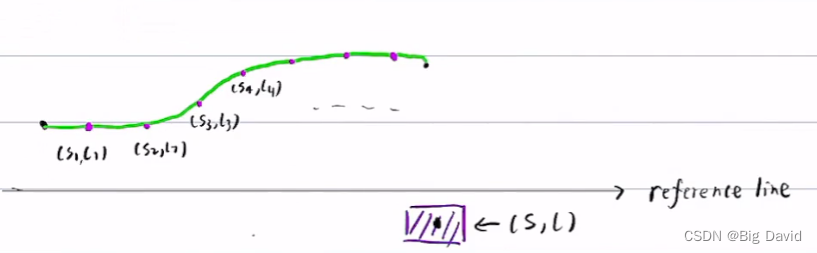
① 平滑代价
f
(
)
f()
f()
越像直线越平滑,两点之间直线最短,期望
∫
(
1
+
f
′
(
x
)
2
)
\int \sqrt{\left(1+f^{\prime}(x)^{2}\right)}
∫(1+f′(x)2)最小,等价于
∫
(
f
′
(
x
)
2
)
\int \sqrt{\left(f^{\prime}(x)^{2}\right)}
∫(f′(x)2)最小,即
∑
f
′
(
s
i
)
2
\sum f^{\prime}\left(s_{i}\right)^{2}
∑f′(si)2最小
② 障碍物距离代价
g
(
)
g()
g()

③ 参考线距离代价
l
(
)
l()
l()
代价函数
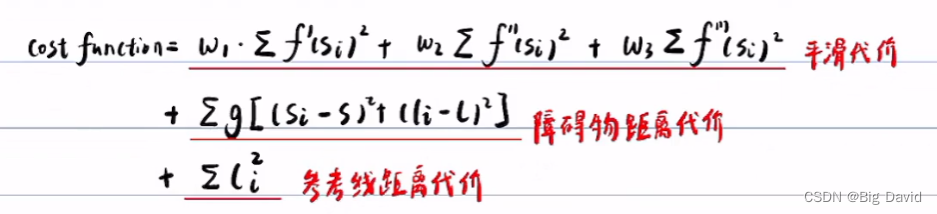
图的最短问题:
① 每个路径都有对应的cost,问题变成了找图最优问题:A*,Dijstra
②EM planner用动态规划解决了这类问题
控制接口:
规划发出的轨迹信息包含
x
,
y
,
θ
,
k
,
v
,
a
,
t
x,y,\theta,k,v,a,t
x,y,θ,k,v,a,t,时间为绝对时间。控制根据当前控制周期的时间搜索轨迹
3.5 自动驾驶之轻决策与重决策
3.5.1 二次规划
求解使二次型 1 2 x T H x + f T x \frac{1}{2}x^THx+f^Tx 21xTHx+fTx值最小的x,并且满足约束 A x ≤ u b Ax≤ub Ax≤ub
无需在意二次规划的约束形式(
l
b
≤
u
b
,
a
≤
b
,
A
x
≤
b
lb≤ub,a≤b,Ax≤b
lb≤ub,a≤b,Ax≤b)
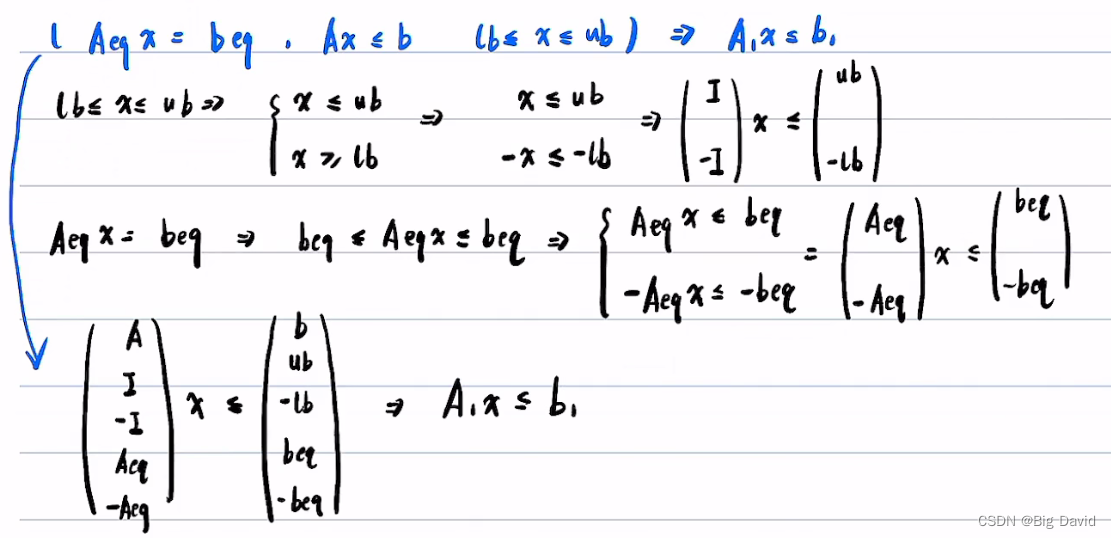
二次规划要求解空间是凸的,而动态规划(决策)开辟了凸空间。

3.5.2 轻决策与重决策
决策算法:轻决策(基于代价函数)和重决策(基于人给定的规则)
重决策

优点:
(1)计算量小
(2)在感知不强的情况下仍然能做决策(融合了人的智慧)
缺点:
(1)场景多无法覆盖
(2)人给出的决策所开辟的凸空间未必满足约束

if-else条件语句,不利于最优控制问题的求解。
轻决策
轻决策:无先验规则,空间离散化,设计cost function,动态规划算法求解离散空间的最优路径,该最优路径开辟凸空间。
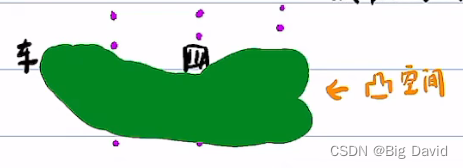
优点:
(1)无人为规则,可以处理复杂场景
(2)有粗解,通过设计代价函数,可以使粗解“满足”硬约束(碰撞、最小曲率),这样使二次规划求解成功的机率大大增加(因为粗解在凸空间内部,所以该凸空间的“扭曲”程度至少有粗解兜底)大大缓解了基于人为规则的决策所造成的凸空间扭曲情况
缺点:
(1)复杂场景计算量很大
(2)依赖预测
(3)对感知,定位要求高
(4)代价函数设计 / 最优解未必符合人的驾驶习惯
L2+ 高速L3 => 重决策
L4 => 轻决策
轻决策和重决策的融合(博弈论)
3.5.3 二次规划算法

l
m
i
n
1
,
l
m
i
n
2
,
.
.
.
,
l
m
a
x
1
.
l
m
a
x
2
,
.
.
.
构成凸空间
l_{min1},l_{min2},...,l_{max1}.l_{max2},...构成凸空间
lmin1,lmin2,...,lmax1.lmax2,...构成凸空间
二次规划的求解空间就在此凸空间中搜索

Apollo 3.5/5.0新增,f(s)尽可能在凸空间的中央
分段加加速度优化法
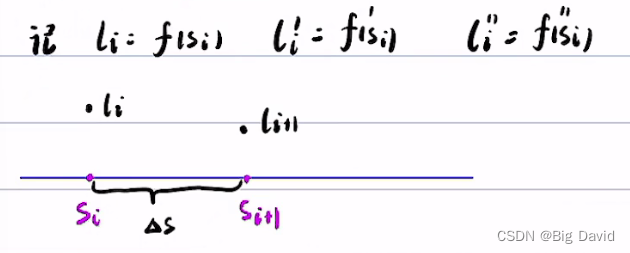

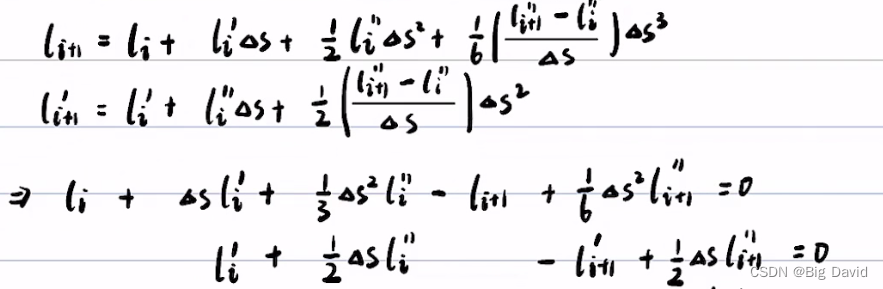
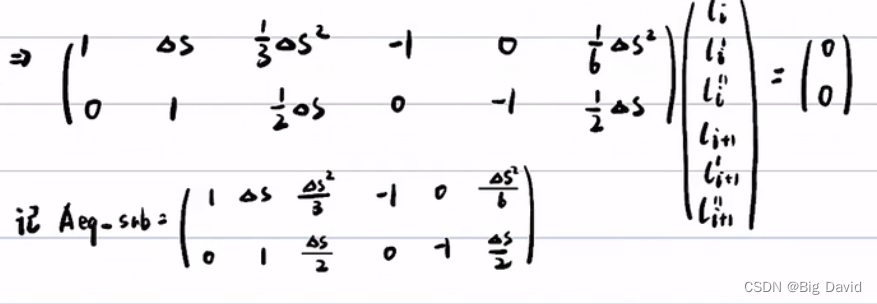
设有
l
1
,
l
1
′
,
l
1
′
′
,
.
.
.
,
l
n
,
l
n
′
,
l
n
′
′
l_1,l_1^{'},l_1^{''},...,l_n,l_n^{'},l_n^{''}
l1,l1′,l1′′,...,ln,ln′,ln′′需要优化
则分段加加速度约束为
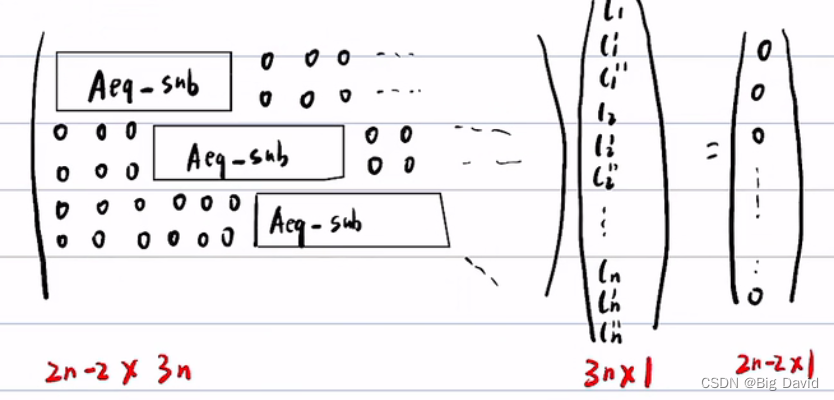
记为
A
e
q
x
=
b
e
q
A_{eq}x=b_{eq}
Aeqx=beq等式约束
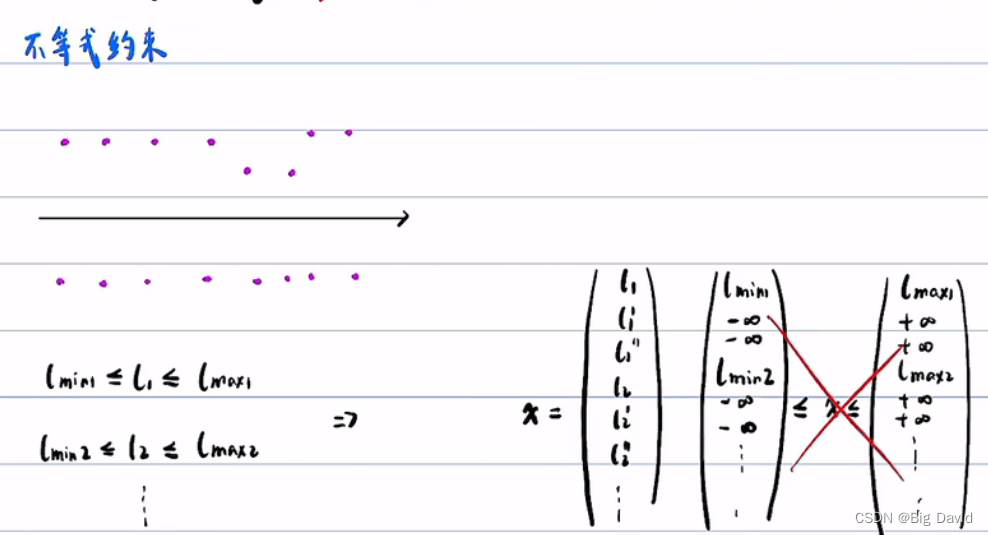
这样做并不准确

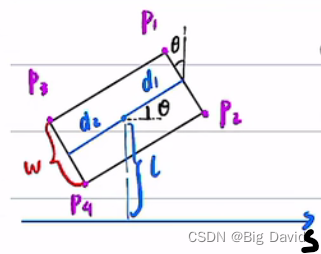
d
1
d_1
d1:汽车质心到车头距离
d
2
d_2
d2:汽车质心到车尾距离
w
w
w:汽车宽度
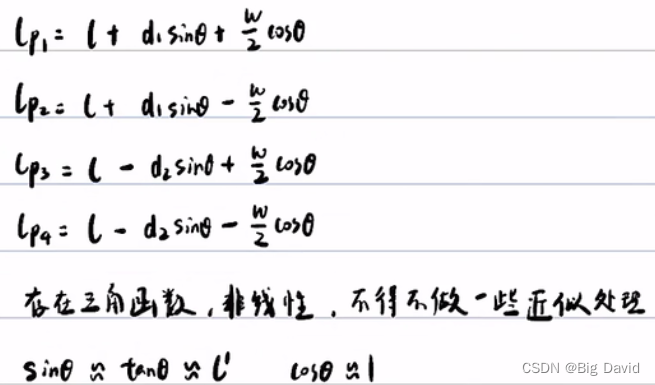




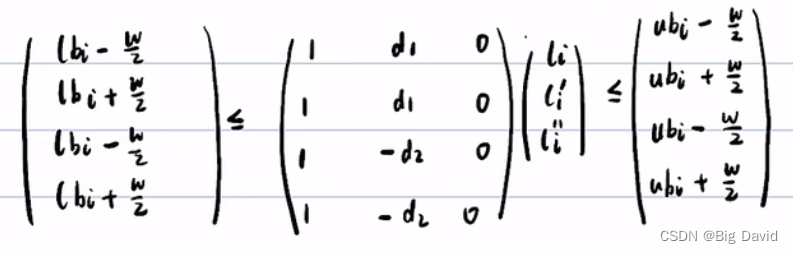

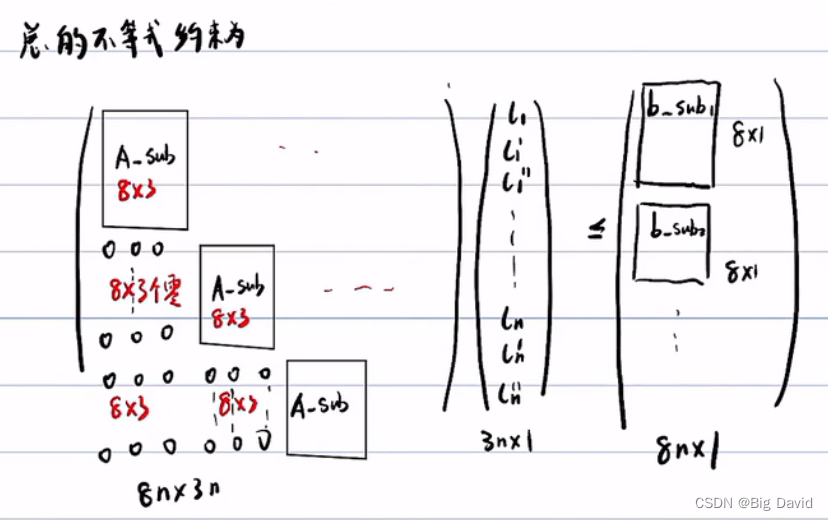
记为
A
x
≤
b
Ax≤b
Ax≤b

求解出
l
1
,
l
1
′
,
l
1
′
′
,
.
.
.
,
l
n
,
l
n
′
,
l
n
′
′
l_1,l_1^{'},l_1^{''},...,l_n,l_n^{'},l_n^{''}
l1,l1′,l1′′,...,ln,ln′,ln′′与
s
1
,
s
2
,
.
.
.
,
s
n
s_1,s_2,...,s_n
s1,s2,...,sn结合即得到二次规划下的最优路径,再转化为Cartesian坐标,路径规划完成。
3.5.4 二次规划崩溃
靠近障碍物时,二次规划崩溃

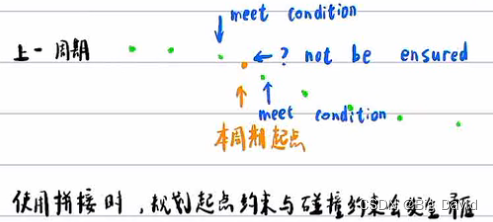
为什么在无避障时不会崩溃?
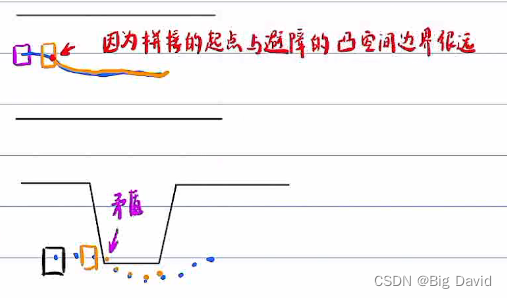
为什么规划的路径会贴着边界?
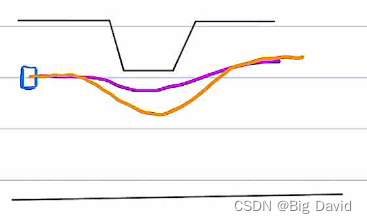
因为二次规划的性质决定,带约束的二次规划最小值只会在极小值点或边界点取得
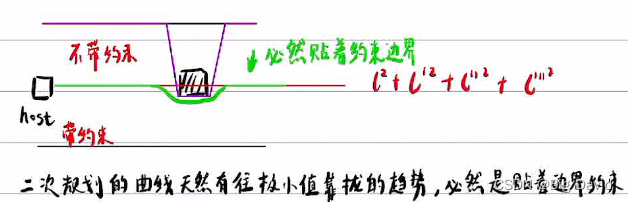
改善二次规划崩溃的方法:
① 规划起点不管了,障碍物放大一点做安全缓冲
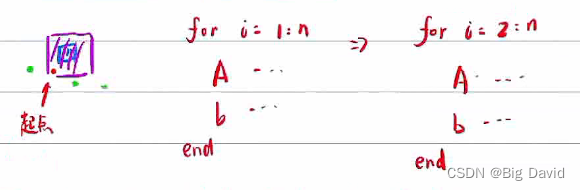
② 改极小值点的位置

c
e
n
t
r
e
l
i
n
e
=
1
2
(
l
m
i
n
+
l
m
a
x
)
centre_{}line=\frac{1}{2}(l_{min}+l_{max})
centreline=21(lmin+lmax)
优点:几何稳定
缺点:
w
c
e
n
t
r
e
w_{centre}
wcentre调小不起明显作用,调大了路径不平滑。
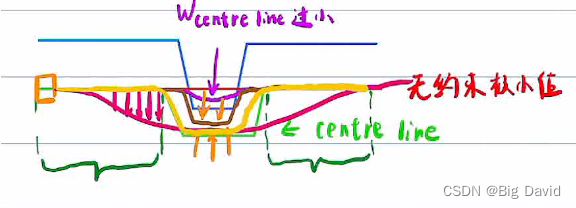

优点:dp曲线平滑相对好做
缺点:
d
p
p
a
t
h
dp_{path}
dppath几何不稳定
dp_path每一帧之间的几何形状都会有巨大变化,若二次规划以dp_path为centre line,qp_path也会震荡。相反,
c
e
n
t
r
e
l
i
n
e
=
1
2
(
l
m
i
n
+
l
m
a
x
)
centre_{}line=\frac{1}{2}(l_{min}+l_{max})
centreline=21(lmin+lmax)就很稳定
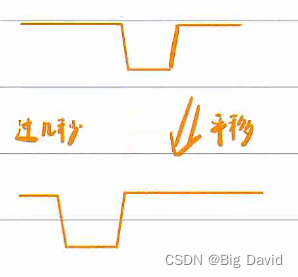
3.5.5 车控制不稳,抖动剧烈
根源:车规划的路径会天然往边界靠拢的趋势
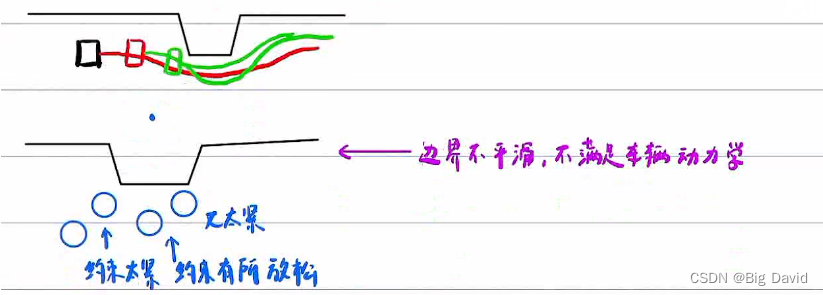
车在边界上当方唐镜,左右横跳。
解决办法:
加不允许反复横跳的约束

新的问题:约束越多,求解越慢
(1)搜索空间增大,需要对更多的可能性进行搜索和验证
(2)约束之间的冲突,需要进行额外的处理来解决这些冲突
(3)优化目标的复杂性,约束条件的增加可能会导致优化目标的复杂性增加
解决:削二次规划的规模,由60 => 20,二次规划求解完毕后再进行插值增密。


3.5.6 决策“朝令夕改”
一会决策向右绕行,一会决策向左绕行

Apollo方法:打标签
这一帧:只对无标签的obs做动态规则决策,若障碍物已经有标签,直接使用标签的决策
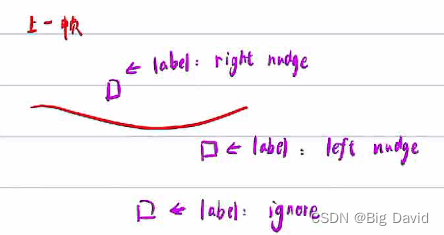
3.5.7 速度规划对路径规划的影响
Path只处理静态障碍物,有问题
这种情况无论速度规划怎么规划,都会碰撞(除非倒车)

已知上一帧的速度规划为10m/s匀速,上一帧的path为直线
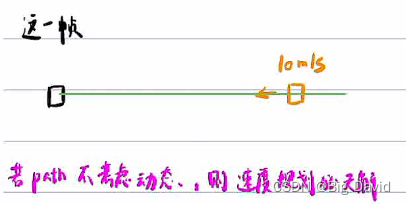
路径规划要拿上一帧的轨迹去判断与动态障碍物的交互

EM planner是SL planning与ST planning反复迭代的过程
上一帧的SL,ST => 当前SL => 当前ST => 下一帧SL
4 SL、ST迭代优化
4.1 ST图、预测
已有cartesian的path,作速度规划

ST图画法
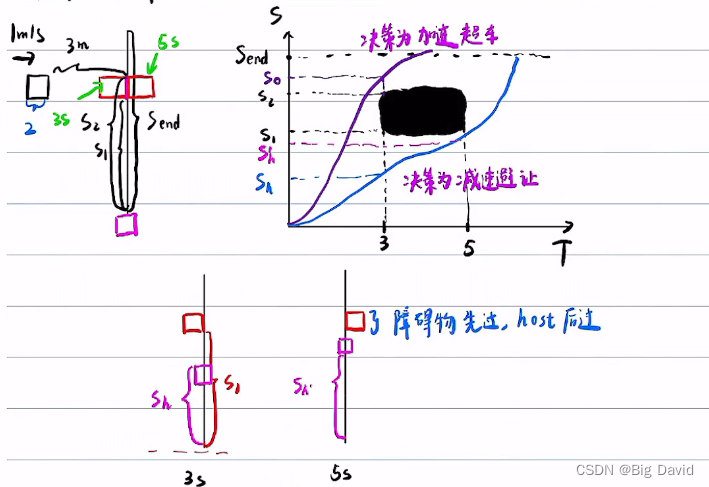
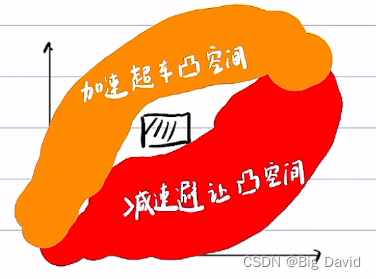
4.2 SL、ST迭代求解
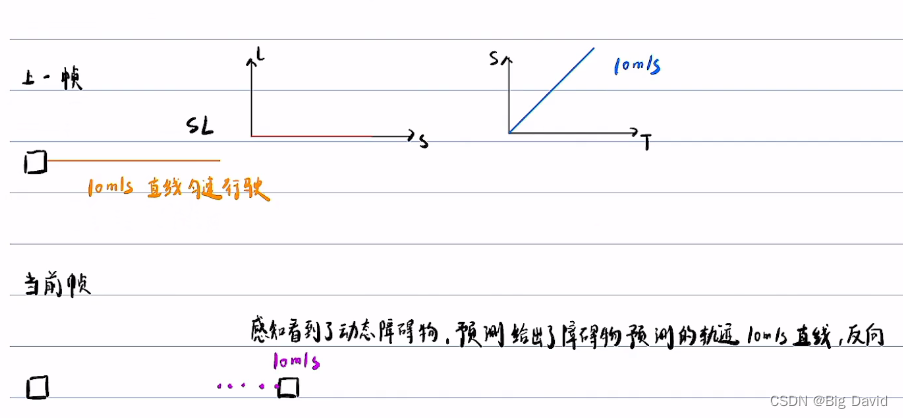
当前帧规划端
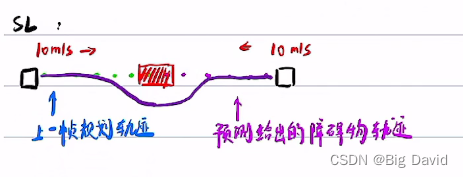
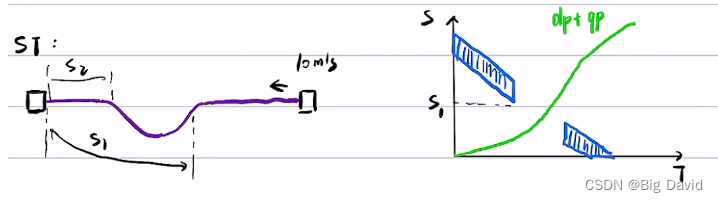
当前帧的规划结果是下一帧的上一次的规划结果
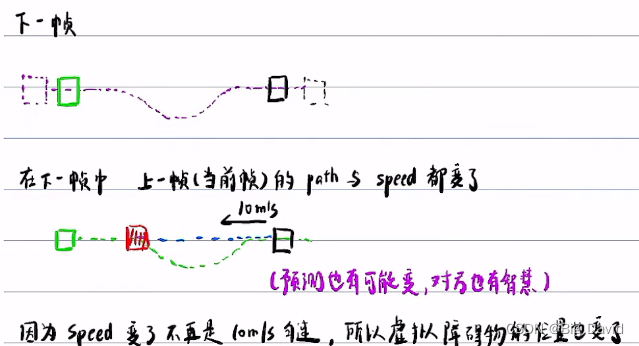
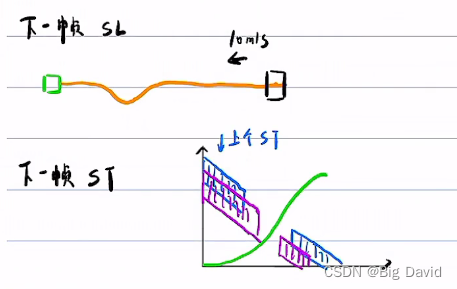
SL、ST迭代过程
上一帧的trajectory + 当前帧的预测 => 当前帧SL的虚拟障碍物 => 当前帧SL(几何受影响)=> 当前帧ST => 改变当前帧ST => 当前帧轨迹trajectory改变
下一帧拿当前帧的trajectory + 下一帧的预测 => 下一帧SL => 下一帧ST
EM planner核心思想
① 将SLT三维规划问题降维,分解成两个二维的SL、ST规划问题大大降低了规划难度
② 上一帧的trajectory优化当前帧的SL、SL优化ST,不断迭代
4.3 SL与ST迭代
规划的基本工具:ST图
ST图依赖预测(预测、博弈、感知最难)
预测模型:恒定
v
⃗
\vec v
v 或者恒定
a
⃗
\vec a
a 模型(简化问题)
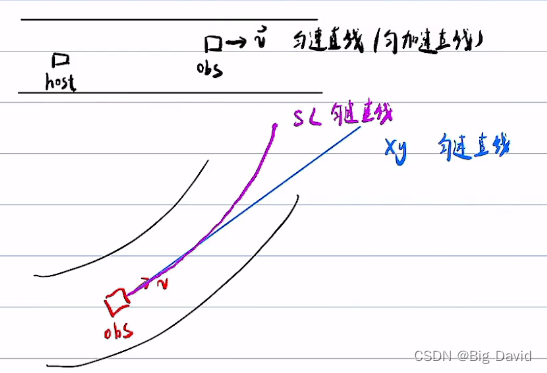
SL、ST迭代问题
Apollo 1.5 EM planner 引入SL,ST解耦规划,凸空间,先决策后规划。在一些复杂工况以及强算力的这个场景下,SL和ST分开优化求解是工业界最广泛最流行的方法。
Apollo 2.5 加入了lattice planner
Apollo 3.5 大幅修改EM planner,变成了public road planner(取消了SL,ST迭代机制,SL只管静态障碍物,ST只管动态障碍物,加入scenario模块)
Apollo 5.0 再次大幅修改public road planner,SL的dp被取消
Apollo 6.0~7.0 改动不大
取消了SL,ST迭代机制:
减轻ST对SL的干扰
因为车的纵向变化能力高于横向,导致动态障碍物车的速度变化剧烈程度远高于路径,预测难以测准,预测不准导致ST图剧烈变化=>速度规划结果剧烈变化
若ST影响SL,会导致SL规划容易不稳定,朝令夕改
车百公里加速:4-5秒 汽油车:5-7秒
百公里刹停距离:32-45m不等
证明汽车在一个非常短的时间、距离内,纵向的速度可以发生剧烈的变化。变化能力远高于横向的。
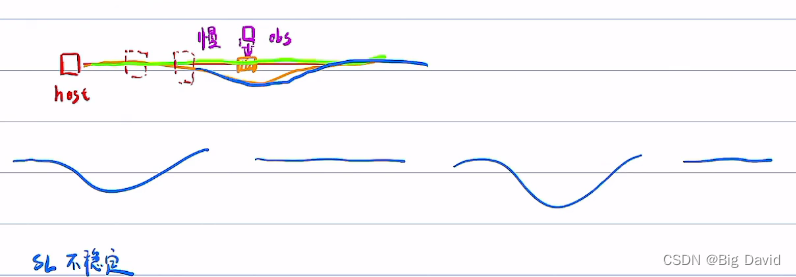
SL只管静态,ST只管动态,是一种兼顾灵活性和稳定性的一种做法
有没有一种方法既能保证路径稳定,又能保证速度稳定,还能应对这个剧烈环境(动态障碍物速度)的剧烈变化,做出相应的完美策略?一般没有。
这种方法SL还是会影响ST,ST不影响SL,因为SL会生成一个路径,路径的几何形状会影响到动态障碍物的交互。所以SL影响ST,ST不影响SL。
有两种场景ST需要影响SL:
① 上一帧的host trajectory与obs trajectory在纵向s有交互的区域内,obs所走过的空间仍然是host不能去的。
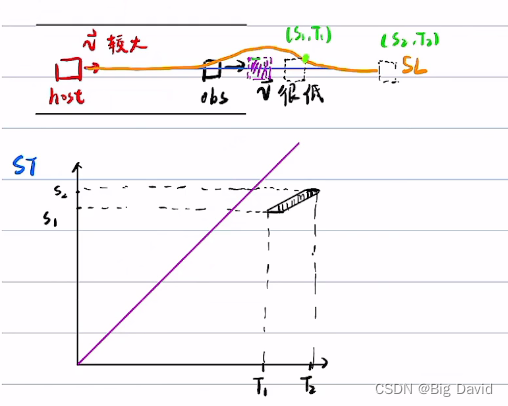
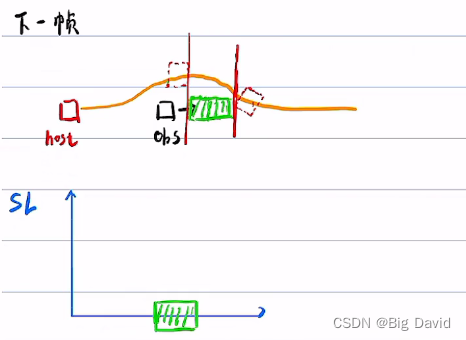
② 纵向有相交,相向而行
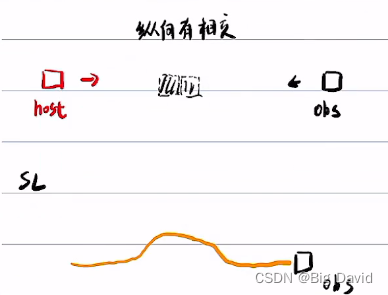
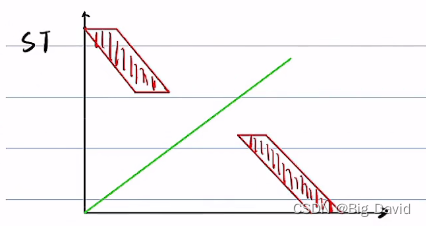
下一帧

特殊情况:

同向而行,动态障碍物很快的方向向前行驶,主车更快,Apollo认为这种情况过于危险,通过变道解决。
百度Apollo EM planner决策规划算法到这里,理论结束。不正之处望读者指教