理解BS期权定价

开局放图

1.完整图示

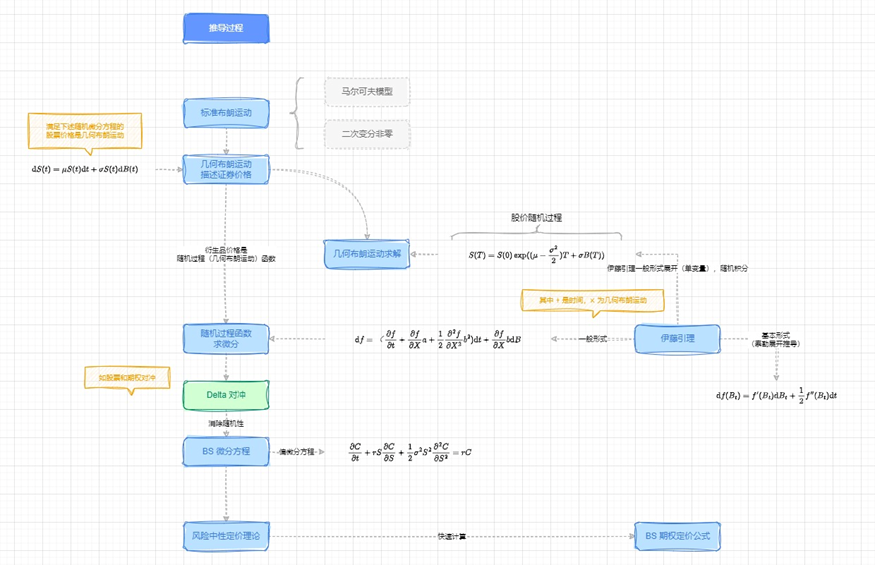
开局一张图！全篇编的尽可能通俗化，有些地方避免不了用公式解释，内容的完整流程图示绘制如下，建议全篇读完后再看流程图。

2.背景知识

期权介绍

首先简单介绍下期权背景知识，期权（Option）是一种赋予期权买方在约定日期以约定的价格买入或卖出约定数量标的资产的权利的合约，而期权卖方必须履行承诺。

按照期权买方执行期权的时限，又可以分成欧式期权和美式期权：1. 欧式期权，即期权买方只能在期权的到期日才能行权的期权；2. 美式期权，即期权买方可以在到期日之前的任一交易日或到期日行权的期权，文章后续内容都假定是欧式期权。按照期权的行权方是买方还是卖方划分：1. 认购期权买方行权，即看涨期权，当 "约定行权价格 + 权利金 < 市场价格" 时盈利，当 "约定行权价格 < 市场价格" 时，即为实值期权，通常买方会行权；2. 认沽期权卖方行权，即看跌期权，显然逻辑相反，文章后续示例假定是看涨期权。

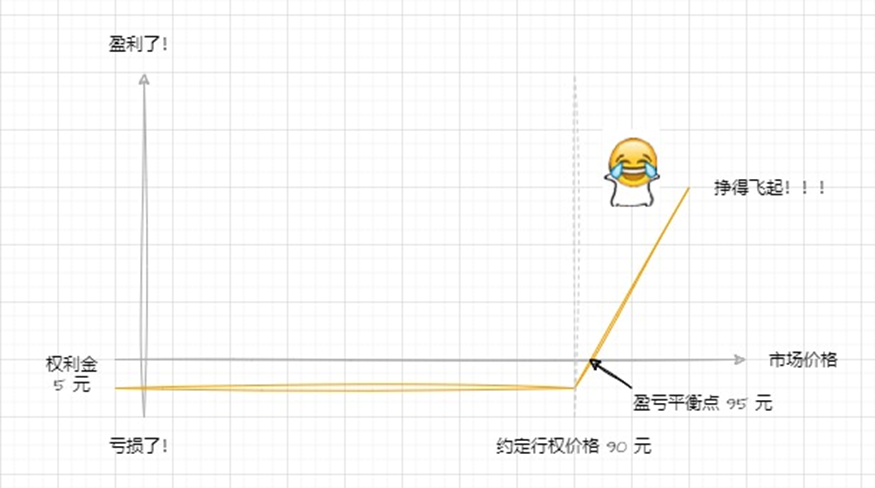
例如：当前某股票期权 A 的价格是 100 元，约定行权的价格是 90 元，权利金是 5 元。假定一年后行权时 A 的市场价格涨到了 120 元，那么此时以 90 元价格行权显然净利润挣了 120-90-5=25 元！！！以上就是简单且非严谨的理解下挣钱利器期权（Option）的概念，示例图如下：

期权定价

文章讨论的是理论模型，即决定期权定多少价合理，定少了都像上面图那样卖出肯定亏死，因此引入文章的主要内容：BS 公式，但是模型的有效性依赖一系列的假设，例如：交易连续发生，资产价格符合几何布朗运动等等。文章比较简单，不展开讨论

原理解析

1.标准布朗运动

布朗运动是一个连续随机过程，什么是随机过程？画了一张图：

沿着竖线看，当 $t=t1$ 时，显然 $X(t1)$ 是一个随机变量，因为变量可能取到不同颜色曲线上的值，同理对于 $X(t2)$ ，这样沿着 $t$ 的无限多个随机变量组成随机过程，因此随机过程是一个整体概念，是多维随机变量的延伸。如果只看一种颜色的曲线，则这条曲线 $x_i(t)$ 对应随机过程的一次全程观测，是关于 $t$ 的函数 $x_i(t)$ ，可理解成把组成随机过程的全部随机变量都采样一次。有没发现单个曲线好像和股票走势长得很像！想象成三条曲线分别对应连续 3 日 0-24 小时的股票走势！

那么布朗运动就是一种特殊的随机过程，又称为维纳过程，这里准确的说是零初值标准布朗运动，具有一系列的特性，比如轨迹会频繁穿越时间轴 $t$ ，且任意时刻不偏离时间轴一个正负标准差 $\sqrt{t}$ ，还是一个马尔可夫过程，即从业务角度理解，布朗运动的当前值包含对其未来做预测所需的全部信息等等，反正更适合描述股票运动，我们记成 $B(t)$ 吧

2.描述股票价格

描述股票收益率

有了标准的布朗运动 $B(t)$ ，继续构建一个带漂移的布朗运动，这样更贴近股票运动的业务特性，无穷小变化量形式如下：

$dX(t)=\mu dt+\sigma dB(t)$

上述是一个随机微分方程，满足均值为 $\mu t$ ，方差为 $\sigma ^2t$ 的正态分布，其中漂移项系数 $\mu$ 是长期平均回报率，即股票期望年收益率， $\sigma$ 是股票年收益率的标准差。这个等式怎么理解？实际上，用上面的 $X(t)$ 描述股票的收益率，可以简单看成收益率曲线在期望年收益率 $\mu$ 上下波动，且不偏离年收益率的标准差 $\sigma$ ，看着符合现实情况，即A股除外股票长期收益是稳定的

$dS(t)/S(t) =\mu dt+\sigma dB(t)\Rightarrow dS(t)=\mu S(t)dt+\sigma S(t)dB(t)$

为什么可以用布朗运动描述收益率？1. 股票的连续复利收益率近似地服从正态分布，和布朗运动一致；2. 布朗运动是一个马尔科夫过程，符合弱式有效市场假说；3. 股票收益率在时间上存在转折尖点，因此与布朗运动处处不可微的特性一致

描述股票价格

我们设股票价格是 $S(t)$ ，使其与收益率公式关联，考虑一个非常小的时间间隔内 $dS(t)$ 为股票价格的变化量，则收益率显然是 $dS(t)/S(t)$ ，结合上面的收益率公式：

$dS(t)/S(t) =\mu dt+\sigma dB(t)\Rightarrow dS(t)=\mu S(t)dt+\sigma S(t)dB(t)$

上面得出无穷小变化量形式的股票价格 $S(t)$

总结：我们得出了股票价格的表达式 $S(t)$ ，用布朗运动 $B(t)$ 进行描述，其自身称为一个几何布朗运动

3.伊藤引理形式

因为布朗运动是一个随机过程，且处处不可微，古典微积分解不出来上面一堆公式，因此需要随机分析知识，伊藤积分则是随机分析的基础，如果不喜欢看推导就直接看章节最后的结论。假定我们有一个关于布朗运动 $B_t$ 的函数 $f(B_t)$ ，按照泰勒展开得到：

$f(B_t+\Delta B_t )-f(B_t )={f}' (B_t )(\Delta B_t )+{f}''(B_t )/2*(\Delta B_t )^{2}+...$

同时布朗运动有个性质，二次变分非零，因此右式第二项不是第一项的高阶无穷小，即(dBt)2=dt，不能够省略掉，得到伊藤引理的基本形式：

$df(B_t )={f}' (B_t )dB_t+1/2 {f}'' (B_t )dt$

上面确实和古典微积分不同。继续推导伊藤引理的一般形式，令 $f(x,X(t))$ 是 $X(t)$ 的二阶连续可导函数，且对 $t$ 一阶可导。首先不限定 $\mu$ 和 $\sigma$ 是常数，假定是时间的函数（其实可以是任意函数），重写 $dX(t)$ 的表达式：

$dX(t)=R_t dt+A_t dB(t)$

然后把 $f$ 按照上面的伊藤引理的基本形式展开：

$df(t,X(t))=\partial f/\partial t dt+df(X(t))=\partial f/\partial t dt+\partial f/\partial X(t) dX(t)+1/2 (\partial ^2 f)/(\partial ^2 X(t) ) (dX(t))^2$

注意上面不能用二次变分直接把 $(dX(t))^2$ 换成 $dt$ ，因为 $X(t)$ 不是 $B_t$ ，实际上

$(dX(t))^2=R_t^2 (dt)^2+A_t^2 (dB(t))^2+2R_t*A_t*dtdB(t)$

右边第1项和第3项是高阶无穷小，直接扔掉，得到

$(dX(t))^2=A_t^2 dt$

再把 $dX(t)$ 代入到f的展开式，得到一般形式：

$df(t,X(t))=(\partial f/\partial t+\partial f/\partial X(t) R_t+1/2 (\partial ^2 f)/(\partial ^2 X(t) ) A_t^2 )dt+\partial f/\partial X A_t dB(t)$

可以看到随机微分方程 $f$ 和 $X$ 的随机性由同一个布朗运动确定，这点非常关键！！！

总结：上面求了一大堆就是让我们具备了展开分析 $df(t,X(t))$ 这个随机微分方程的能力。应用随机积分还能得出上面股票价格关于时间的变化函数 $S(t)$ ，此处不再详细解释过程，假定已经计算出了 $S(t)$

4.BS公式

上面内容都有了，现在假定 $C(t,S(t))$ 是欧式看涨期权的价格，是时间t和股票价格S(t)的函数，观察发现是不是可以按照伊藤引理一般形式展开：

$dC=(\partial C/\partial S \mu S+\partial C/\partial t+1/2 (\partial ^2 C)/(\partial S^2 ) \sigma ^2 S^2 )dt+\partial C/\partial S \partial SdB$

之前提到伊藤过程 $X$ 的函数 $f$ 和 $X$ 的随机性来自同一个布朗运动，结合之前 $dS=\mu Sdt+\sigma SdB$ 的定义，观察很小时间区间 $\Delta t$ 内股价 $\Delta S$ 和期权价格 $\Delta C$ 的关系，两个公式都看最后一项，发现啊！！！做空1份期权，同时做多 $\partial C/\partial S$ 份股票，组合两个公式后随机因子 $dB$ 就没有了，即我们的投资组合结果是确定的，这种方式就是Delta对冲

如果采用上面的股票和期权投资组合， $\Delta t$ 时间内对冲后的结果是：

$\Delta R=-\Delta C+\partial C/\partial S \Delta S=(-\partial C/\partial t-1/2 (\partial ^2 C)/(\partial S^2 ) \sigma ^2 S^2 )\Delta t$

而投资组合的价值是当前做空期权价值加上做多股票价值：

$R=-C+\partial C/\partial S S$

结合理论：市场中不存在无风险套利机会时，投资组合在Δt时间内的收益率等于无风险收益率 $r$ ，即表示成 $\Delta R=rR\Delta t$ ，进一步组合全部公式，就得到了BS微分方程：

$\partial C/\partial t+rS \partial C/\partial S+1/2 \sigma ^2 S^2 (\partial ^2 C)/(\partial S^2 )=rC$

上面就是个普通微分方程，描述股票和期权的投资组合，随机因子被对冲掉了，因为已假定上面 $S(t)$ 的价格已经用随机积分求解完了，这里可以求解出 $C$ ，即期权定价多少钱比较好 #_#，大概原理就是上面这些

编写代码

直接写代码收尾，还有一大堆理论的东西解释起来太麻烦，不如直接跑代码拿结果。因为由上面的 BS 公式可以得到风险中性定价理论，即可以用无风险收益率 $r$ 对衍生品收益期望进行贴现，从而简化求解过程，得到一组快速求解公式，这里不再列出公式，最终计算出期权理论价格只需要五个变量：当前股价 $S(0)$ ，行权价格 $K$ ，行权日到当前的年单位时间 $T$ ，无风险收益率 $r$ ，标的股票的年收益率的标准差 $\sigma$

代码中的函数 _volatility 结果就是对应的 $\sigma$ ，即计算年收益率的标准差。完整如下：

from typing import (
    Union,
    Sequence
)
from datetime import datetime

import numpy as np
import pandas as pd
from scipy.stats import norm

TableData = Union[pd.DataFrame, np.ndarray, Sequence[Sequence]]


class BSM:

    def __init__(self, data: TableData, data_column: int = 0, data_cycle: int = 365):
        self.__data = data
        self.__data_column = data_column
        self.__data_cycle = data_cycle

    def pricing_merton(self, S: float, K: float, r: float, T0: datetime, T1: datetime, otype: str = 'call') -> float:
        """BSM 期权定价

        Args:
            S: 股票当前价格
            K: 期权行权价格
            r: 股票无风险收益率
            T0: 期权定价日期
            T1: 期权行权日期
            otype: 期权类型（call or put）

        Returns:
            价格
        """
        if otype != 'call' and otype != 'put':
            raise ValueError('The parameter value of `otype` is illegal')

        sigma = self._volatility()
        return self._price(S, K, sigma, r, T0, T1, otype)

    def _price(self, S: float, K: float, sigma: float, r: float, T0: datetime, T1: datetime, otype: str) \
            -> float:

        T = (T1 - T0).days / 365
        d1 = (np.log(S / K) + (r + pow(sigma, 2) / 2) * T) / (sigma * np.sqrt(T))
        d2 = d1 - sigma * np.sqrt(T)

        if otype == 'call':
            # Call option
            value_c = S * norm.cdf(d1) - K * np.exp(-r * T) * norm.cdf(d2)
            return value_c
        else:
            # Put option
            value_p = K * np.exp(-r * T) * norm.cdf(-d2) - S * norm.cdf(-d1)
            return value_p

    def _volatility(self) -> float:
        rate = np.log(self.__data.iloc[:, self.__data_column] / self.__data.iloc[:, self.__data_column].shift(1))
        rate = rate.dropna()
        rate_volatility = np.sqrt(self.__data_cycle) * rate.std()

        return rate_volatility