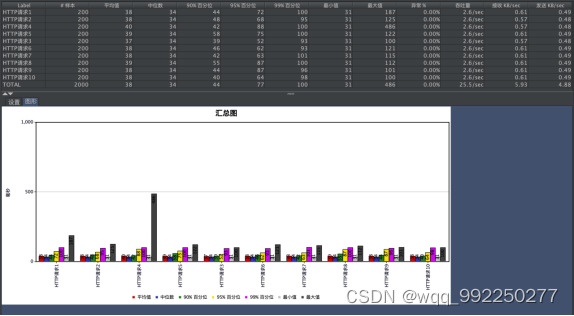
TOC
- 1 前言
- 2 方法
- 2.1 LOW-RANK-PARAMETRIZED UPDATE MATRICES
1 前言
1) 提出背景
大模型时代,通常参数都是上亿级别的,若对于每个具体任务都要去对大模型进行全局微调,那么算力和资源的浪费是巨大的。
根据流形学习思想,对于数据有用的特征通常集中于低维流形区域。我们想去微调,实际上只是让部分特征的权值更大而已,而这部分特征也是低维的,我们没有必要小题大做将整个模型的参数都动一遍。
鉴于此思想,提出了LoRA(Low - Rank Adaptation), 既冻结住预训练好的大模型,插入可训练低维压缩矩阵到每一层(本文是插入到transformer层)。我们仅仅去微调插入的可学习矩阵,这样既可以显著降低需要微调的参数量,同时也不会增加额外的推理时间。
2 方法
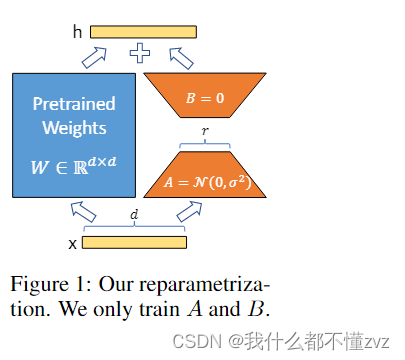
2.1 LOW-RANK-PARAMETRIZED UPDATE MATRICES
- 对于整个预训练大模型可以看作是 W 0 d × k W_0^{d\times k} W0d×k,既输入是一个 d d d维tensor,输出一个 k k k维tensor;
- 对于新增的矩阵, A d × r A^{d\times r} Ad×r, B r × k B^{r\times k} Br×k, 其中 r r r就是low rank, r < < m i n ( d , k ) r<<min(d,k) r<<min(d,k)。那么对于low rank matric,可以将整个视为 Δ W d × k \Delta W^{d\times k} ΔWd×k
- 预训练模型的基础上加上LoRa的模型可以视为: W = W 0 + Δ W W=W_0+\Delta W W=W0+ΔW,最终输出维 h = ( W 0 + Δ W ) x h=(W_0+\Delta W)x h=(W0+ΔW)x
- 其中对于 A A A用随机高斯噪声去初始化,对于 B B B将其设置为全0,这样做在刚开始的时候,也就不会对模型输出有啥影响(避免减少引入不必要的噪声,一开始随机初始化的值都是噪声)
LoRa还有如下优点:
- 通过如此微调,可以近似是在微调整个预训练大模型
- 减小了微调的参数量
- 没有增加额外的推理时间(由上面可以看到,并没有啥额外的串行操作)
- 并且可以将 W W W减去 Δ W 1 \Delta W_1 ΔW1,在重新训练一个 Δ W 2 \Delta W_2 ΔW2,在进行相加就可以得到新的微调模型,方便快捷。