线性回归

代码过程

训练过程：

1. 准备数据集
2. 设计模型（用来计算 $\hat{y}$）
3. 构造损失函数和优化器（API）
4. 训练周期（前馈、反馈、更新）

准备数据

这里的输入输出数据均表示为3×1的，也就是维度均为1

# 行表示实例数量，列表示维度feature
import torch
x_data=torch.Tensor([[1.0],[2.0],[3.0]])
y_data=torch.Tensor([[2.0],[4.0],[6.0]])

设计模型

模型继承Module类，并且必须要实现 init 和 forward 两个方法，其中self.linear=torch.nn.Linear(1,1)表示实例化Linear类，这个类是可调用的，其__call__函数调用了 forward 方法

class LinearModel(torch.nn.Module):
    def __init__(self):
        super(LinearModel,self).__init__()
        # weight 和 bias 1 1 
        self.linear=torch.nn.Linear(1,1)
        
    def forward(self,x):
        # callable
        y_pred=self.linear(x)
        return y_pred

# callable
model=LinearModel()

pytorch中的linear类是在某一个数据上应用线性转换，其公式表达为 $y=x{w}^T+b$

class torch.nn.Linear(in_features,out_features,bias=True) ：其中in_features和out_features分别表示输入和输出的数据的维度（列的数量），bias表示偏置，默认是true，该类有两个参数

• weight：可学习参数，值从均匀分布$U(-\sqrt{k},\sqrt{k})$中获取，其中 $k=\frac{1}{in\_features}$
• bias：shape和输出的维度一样，也是从分布$U(-\sqrt{k},\sqrt{k})$中初始化的
  

设计构造函数与优化器

# 构造损失函数和优化器
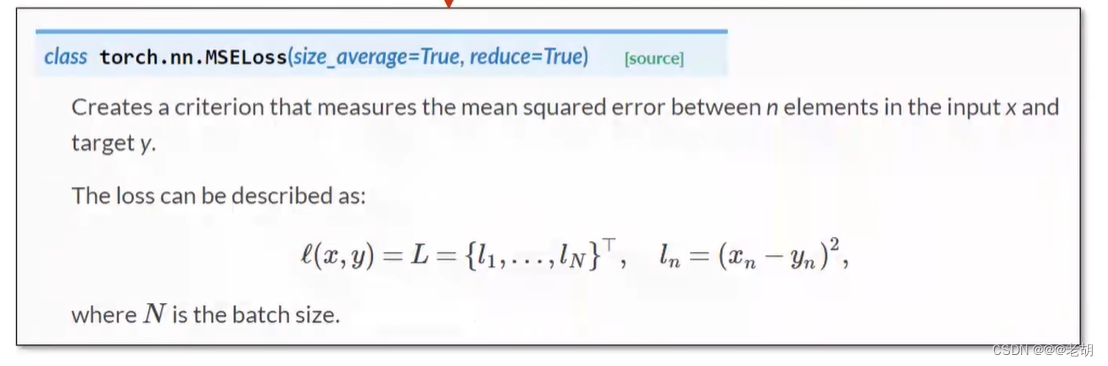
criterion=torch.nn.MSELoss(size_average=False)

# w和b--->parameters
opyimizer=torch.optim.SGD(model.parameters(),lr=0.01)

训练过程

# 训练过程
for epoch in range(100):
    y_pred=model(x_data)
    loss=criterion(y_pred,y_data)
    # loss标量，自动调用__str__()
    print(epoch,loss)
    
    optimizer.zero_grad()
    # backward
    loss.backward()
    # update
    optimizer.step()

训练代码和结果

# 行表示实例数量，列表示维度feature
import torch
x_data=torch.Tensor([[1.0],[2.0],[3.0]])
y_data=torch.Tensor([[2.0],[4.0],[6.0]])

class LinearModel(torch.nn.Module):
    def __init__(self):
        super(LinearModel,self).__init__()
        # weight 和 bias 1 1 
        self.linear=torch.nn.Linear(1,1)
        
    def forward(self,x):
        # callable
        y_pred=self.linear(x)
        return y_pred

# callable
model=LinearModel()

# 构造损失函数和优化器
criterion=torch.nn.MSELoss(size_average=False)
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)

# 训练过程
for epoch in range(100):
    y_pred=model(x_data)
    loss=criterion(y_pred,y_data)
    # loss标量，自动调用__str__()
    print(epoch,loss)
    
    optimizer.zero_grad()
    # backward
    loss.backward()
    # update
    optimizer.step()
    
    
# 打印信息
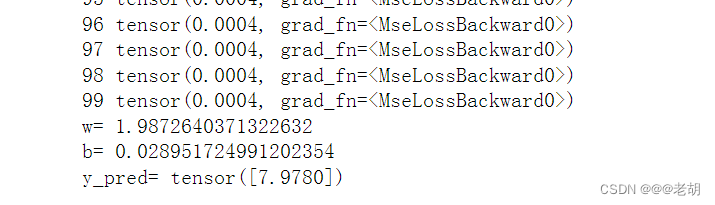
print('w=',model.linear.weight.item())
print('b=',model.linear.bias.item())

x_test=torch.Tensor([4.0])
y_test=model(x_test)
print('y_pred=',y_test.data)

---

pytorch中的Linear层的底层原理（个人喜欢，不用看）

我们在课本使用到的线性函数的基本公式表达为$y=x{w}^T+b$，但是在Linear层中，当输入特征被Linear层接收是，它会接收后转置，然后乘以权重矩阵，得到的是输出特征的转置，换句话说可以在底层使用Linear，它实际上做的是$y^T=w{x}^T+b$。可以使用下面的案例进行验证：

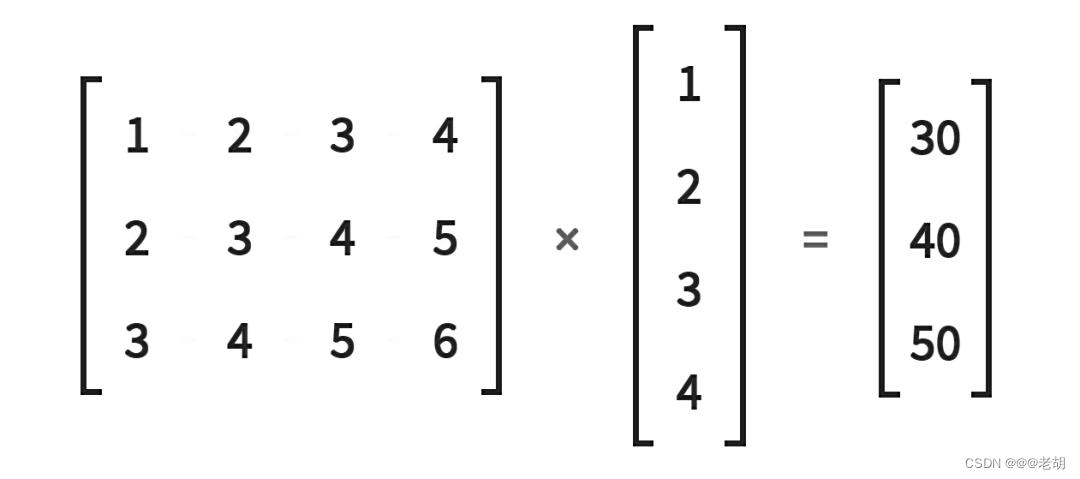
普通矩阵乘法实现

很明显，上面的图标表示一个 3×4 的矩阵乘以 4×1 的矩阵，得到一个 3×1 的输出矩阵，使用普通矩阵的乘法实现如下。

import torch

in_features=torch.tensor([1,2,3,4],dtype=torch.float32)
weight_matrix=torch.tensor([
    [1,2,3,4],
    [2,3,4,5],
    [3,4,5,6]
],dtype=torch.float32)

weight_matrix.matmul(in_features)# 矩阵乘法

实现截图：

Linear层实现

# 这里还是使用上面使用过的数据
import torch
in_features=torch.tensor([1,2,3,4],dtype=torch.float32)
weight_matrix=torch.tensor([
    [1,2,3,4],
    [2,3,4,5],
    [3,4,5,6]
],dtype=torch.float32)

print(weight_matrix.matmul(in_features))# 矩阵乘法

fc = torch.nn.Linear(in_features=4, out_features=3, bias=False)
# 这里是随机一个权重矩阵
print('fc.weight',fc.weight)
fc(in_features)

输出结果：

print('fc.weight',fc.weight)

# 使用上面的权重矩阵进行计算
fc.weight = torch.nn.Parameter(weight_matrix)
print('fc.weight',fc.weight)
fc(in_features)

结果截图：

可以看到上面截图与下面的截图的区别，一开始随机一个权重的时候，进行运算，使用到前面提及到的权重矩阵后，Linear层进行运算之后，得到与使用普通矩阵乘法一样的结果，相同的结果说明，Linear底层的实现与上面的矩阵乘法的逻辑是一致的。

以上的论证可以说明，Linear的底层实现其实是$y^T=w{x}^T+b$，而不是$y=x{w}^T+b$，可能会有人好奇，为什么书本上都是写的后者而不是写前者，其实本质上二者都一样，前者的转置就是后者。

回调机制

在pytorch学习（一）线性模型中，第一个代码中，我们没有通过pytorch实现线性模型的时候，我们会显式调用forward函数，计算前馈的值，我们是这样写的y_pred_val=forward(x_val)，但是在使用pytorch之后，我们是这样写的y_pred=model(x_data)，直接实例化一个对象，然后通过对象直接计算预测值（前馈值），但是并没有使用到forward函数。这是因为pytorch模块类中实现了python中一个特殊的函数，也就是回调函数。

如果一个类实现了回调方法，那么只要对象实例被调用，这个特殊的方法也会被调用。我们不直接调用forward()方法，而是调用对象实例。在对象实例被调用之后，在底层调用了__ call __方法，然后调用了forward()方法。这适用于所有的PyTorch神经网络模块。

以上仅代表小白个人学习观点，如有错误欢迎批评指正。

参考

---

---

逻辑斯蒂回归

逻辑斯蒂回归解决的事分类问题，分类输出的是类别的概率

模型

在线性模型中，通过$y=wx+b$输出的是一个实数值，但是在分类问题中，输出的是类别的概率，所以需要一个函数，把实数值映射到[0,1]之间，表示概率，这个函数为 sigmoid 函数$y=\frac{1}{1+e^{-x}}\in [0,1]$，sigmoid函数属于饱和函数。

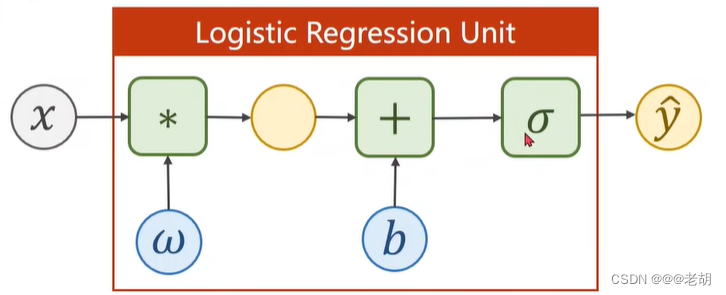
以上，逻辑斯蒂回归模型的公式为：$\hat{y}=\sigma (x\ast w+b)$

损失函数

在线性回归中，计算损失一般是使用均方误差(预测值与真实值的差值的平方和的累加)，在回归问题中，均方误差表示数轴上两个值之间的距离，但是分类问题中，输出的结果表示的是概率（分布），使用距离是没有意义的，所以分类问题中的损失函数并不是均方误差。

在逻辑斯蒂回归中，使用的是BCE

代码和结果

import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt


x_data=torch.Tensor([[1.0],[2.0],[3.0]])
y_data=torch.Tensor([[0],[0],[1]])

class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel,self).__init__()
        self.linear=torch.nn.Linear(1,1)
        
    def forward(self,x):
        y_pred=F.sigmoid(self.linear(x))
        return y_pred
    
model=LogisticRegressionModel()

# 损失函数
criterion=torch.nn.BCELoss(size_average=False)
# 优化器
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)

# 训练
for epoch in range(1000):
    y_pred=model(x_data)
    loss=criterion(y_pred,y_data)
    print(epoch,loss.item())
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
# linspace与range函数类似，用于生成均匀分布的数值序列
# np.linspace(start=0,stop=10,num=200)
x=np.linspace(0,10,200)
# 数据集，test，生成200*1的矩阵
x_t=torch.Tensor(x).view((200,1))
y_t=model(x_t)
y=y_t.data.numpy()
plt.plot(x,y)
plt.plot([0,10],[0.5,0.5],c='r')
plt.xlabel("Hours")
plt.ylabel("Probability of Pass")
# 显示网格线
plt.grid()
plt.show()