✨冒泡
✨选择
✨插入
✨标准写法
🎭不同写法
✨希尔排序——标准写法
✨快排
✨归并
✨堆排

✨冒泡

void Bubble(vector<int>& nums)
{
// 冒泡排序只能先确定最右边的结果,不能先确定最左边的结果
for (int i = 0; i < nums.size(); i++)
{
// 确定的右边的就不用排了并且不能让j+1越界
// 所以判断条件是nums.size()-i - 1
for (int j = 0; j < nums.size()-i - 1; j++)
if (nums[j] > nums[j + 1])
swap(nums[j], nums[j + 1]);
}
}
✨选择
选择排序重要的是选,先选出来,再将这个数交换进去

void Select(vector<int>& nums)
{
for (int i = 0; i < nums.size(); i++)
{
int t = i;// 记录需要交换的数的位置
for (int j = i + 1; j < nums.size(); j++)
if (nums[t] > nums[j])
t = j;
swap(nums[t], nums[i]);
}
}
✨插入

✨标准写法
插入排序是一个一个往后挪,最后再插入
void Insert(vector<int>& nums)
{
for (int i = 0; i < nums.size(); i++)
{
int t = nums[i];
// 注意j表示需要检查的位置,这个位置必须遵循j>=0
for (int j =i-1; j >= 0; j--)
{
if (nums[j] > t)
nums[j + 1] = nums[j];
else
{
nums[j + 1] = t;
break;
}
}
}
}
注意j的范围
🎭不同写法
这种写法类似于冒泡排序,他是往前冒,虽然能对,但是这已经不是插入排序的思想
int* sortArray(int* nums, int numsSize, int* returnSize)
{
//插入排序:在已经排好序的数组中进行插入
*returnSize=numsSize;
for(int i=0;i<numsSize;i++)
{
//从此位置向前比
for(int j=i;j>0;j--)
{
if(nums[j]<nums[j-1])
{
int tem=nums[j];
nums[j]=nums[j-1];
nums[j-1]=tem;
}
else
break;
}
}
return nums;
}
✨希尔——标准写法

希尔排序是在插入排序的基础上发展而来,所以要遵循插入排序的逻辑
他和插入排序不同在于,插入排序的gap=1,这个gap是从大到小变化
void Shell(vector<int>& nums)
{
for (int gap = nums.size()/2; gap >0; gap/=2)// 间隔
{
//每次向后跳间隔个长度
for (int i = 0; i < nums.size(); i++)
{
int t = nums[i];
// 注意j的范围
for (int j = i-gap; j >= 0; j -= gap)
{
if (nums[j] > t)
nums[j + gap] = nums[j];
else
{
nums[j + gap] = t;
break;
}
}
}
}
}
注意j的范围
✨快排
我们使用三段式进行排序
[l,left] [left+1,right-1] [right,r]
[l,left]——小于key
[left + 1 , right-1]—— 等于key,等于key的是不用排序
[right , r]——大于key
int getNum(vector<int>& nums, int l, int r)
{
srand(time(nullptr));
return nums[l + rand() % (r - l + 1)];
}
void quicksort(vector<int>& nums, int l, int r)
{
if (l >= r) return;
int key = getNum(nums, l, r);
int left = l - 1, right = r + 1, g = l;// 采用三段式进行
while (g < right)
{
if (nums[g] == key) g++;
else if (nums[g] < key) swap(nums[g++], nums[++left]);
else swap(nums[g], nums[--right]);
}
// [l,left][left+1,right-1][right,r]
quicksort(nums, l, left), quicksort(nums, right, r);
}
✨归并
归并排序需要一个辅助数组,我们使用的是vector,使用之前需要进行resize,开足够大的空间的同时要运行进行随机访问
vector<int> tem;
void mergesort(vector<int>& nums, int l, int r)
{
if (l >= r) return;
int mid = l + r >> 1;
mergesort(nums, l, mid), mergesort(nums, mid + 1, r);
int left = l, right = mid + 1;
int t = 0;
while (left <= mid && right <= r)
{
if (nums[left] < nums[right]) tem[t++] = nums[left++];
else tem[t++] = nums[right++];
}
while (left <= mid) tem[t++] = nums[left++];
while (right <= r) tem[t++] = nums[right++];
t = 0;
left = l;
while (left <= r) nums[left++] = tem[t++];
}
堆排
void up(vector<int>& nums,int t)
{
while (t > 0)
{
int parent = (t - 1) / 2;
// 大根堆
if (nums[parent] < nums[t])
swap(nums[parent], nums[t]);
t = parent;
}
}
void down(vector<int>& nums,int t)
{
// 需要从这个位置开始向下down到底
int child = t * 2 + 1;
while (child < nums.size())
{
// 找到左右孩子中最小的位置
//if (child + 1 < nums.size() && nums[child] > nums[child + 1])
// child++;
//if(nums[t]>nums[child])
// swap(nums[t], nums[child]);
if (child + 1 < nums.size() && nums[child] < nums[child + 1]) child++;
if (nums[t] < nums[child])
swap(nums[t], nums[child]);
t = child;
child = t * 2 + 1;
}
}
void Heap(vector<int>& nums)
{
//筛选法建立初始堆——小大根堆都可以
//for (int i = nums.size()/2; i >= 0; i--) down(nums, i);
//for (int i = 0 ; i < nums.size(); i++) up(nums, i);// 如果想用up初始化堆,只能从头开始
}
筛选法建堆——先将所有数据加入构成堆,在从中间位置开始进行down(只能down,不论是建大堆还是小堆)
什么时候使用up,为什么up不能在筛选法建堆中使用
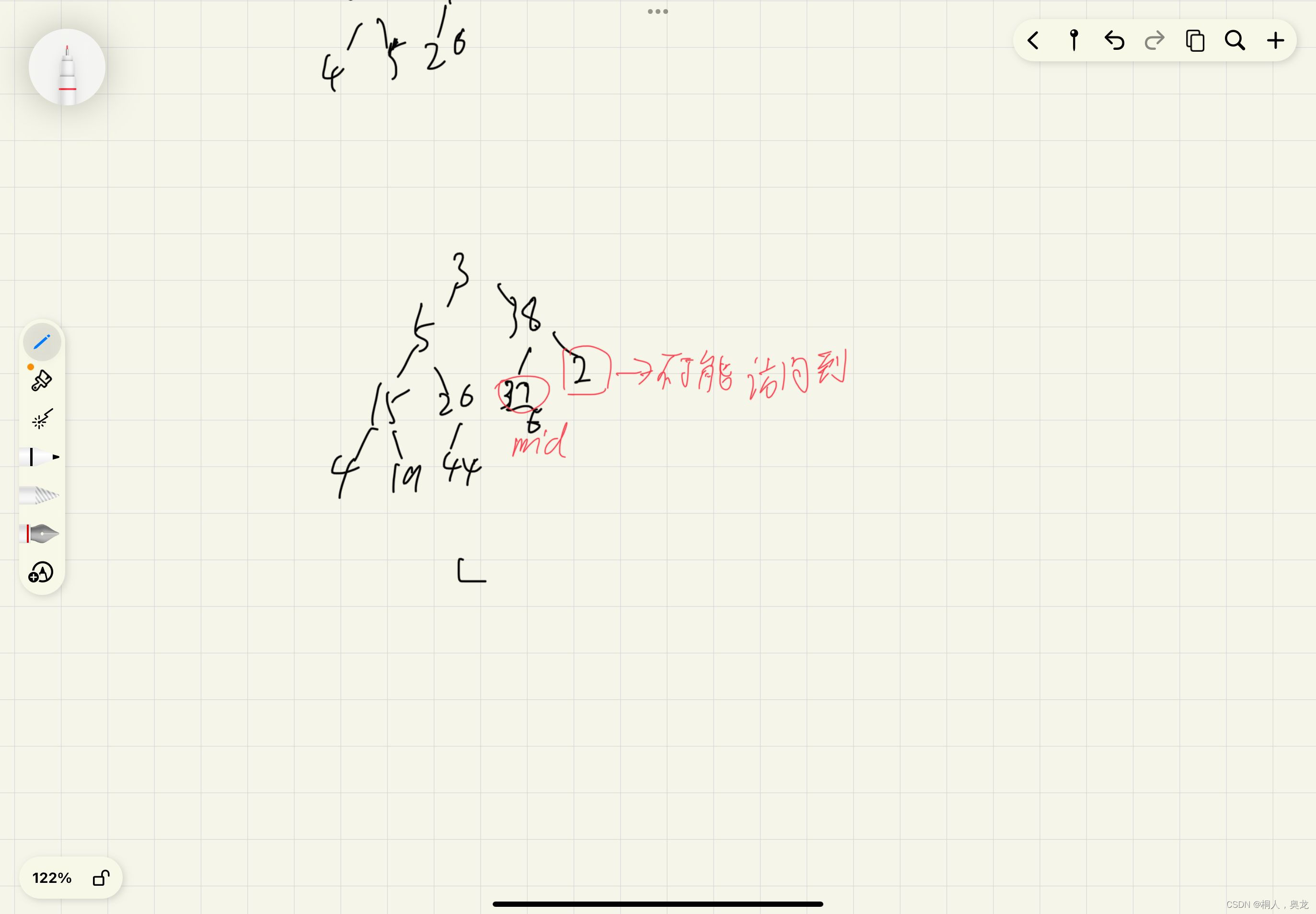
就像上图中的情况,在建小堆的过程中,2是一定不能访问到的,就不能建成小堆,所以不能在筛选法中使用up(关键是筛选法起点是中间位置)
如果想使用up,必须将每一个进行up,或者是某个位置上面的已经成堆,那么就可以在这个位置直接使用up
对于down来说,如果某个位置下面已经成堆,那么就可以直接使用down









![[密码学]Base64编码](https://img-blog.csdnimg.cn/direct/468ef1c610474b11977ef83b992d6e78.png)