机器学习面经系列的其他部分如下所示:
机器学习-面经(part1)
机器学习-面经(part2)-交叉验证、超参数优化、评价指标等内容
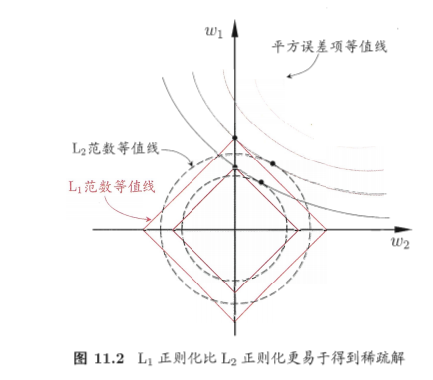
机器学习-面经(part3)-正则化、特征工程面试问题与解答合集
机器学习-面经(part4)-决策树共5000字的面试问题与解答
机器学习-面经(part5)-KNN以及SVM等共二十多个问题及解答
机器学习-面经(part6)-集成学习(万字解答)
11 无监督学习
11.1 聚类
原理:对大量未知标注的数据集,按数据的内在相似性将数据集划分为多个类别,使类别内的数据相似度较大而类别间的数据相似度较小。
聚类的应用场景: 求职信息完善(有大约10万份优质简历,其中部分简历包含完整的字段,部分简历在学历,公司规模,薪水,等字段有些置空顶。希望对数据进行学习,编码与测试,挖掘出职位路径的走向与规律,形成算法模型,在对数据中置空的信息进行预测。)
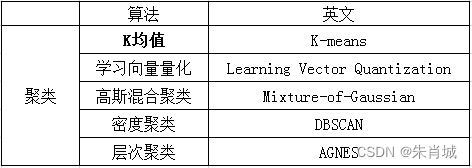
11.1.1 K-means
定义:也叫K均值或K平均。通过迭代的方式,每次迭代都将数据集中的各个点划分到距离它最近的簇内,这里的距离即数据点到簇中心的距离。
K-means步骤:
1.随机初始化K个簇中心坐标
2.计算数据集内所有点到K个簇中心的距离,并将数据点划分近最近的簇
3.更新簇中心坐标为当前簇内节点的坐标平均值
4.重复2、3步骤直到簇中心坐标不再改变(收敛了)
11.1.1.1 K值的如何选取?
K-means算法要求事先知道数据集能分为几群,主要有两种方法定义K。
elbow method通过绘制K和损失函数的关系图,选拐点处的K值。
经验选取人工据经验先定几个K,多次随机初始化中心选经验上最适合的。
通常都是以经验选取,因为实际操作中拐点不明显,且elbow method效率不高。
11.1.1.2 K-means算法中初始点的选择对最终结果的影响?
K-means选择的初始点不同获得的最终分类结果也可能不同,随机选择的中心会导致K-means陷入局部最优解。解决方案包括多次运行算法,每次用不同的初始聚类中心,或使用全局优化算法。
11.1.1.3 K-means不适用哪些数据?
1.数据特征极强相关的数据集,因为会很难收敛(损失函数是非凸函数),一般要用Kernal K-means,将数据点映射到更高维度再分群。
2.数据集可分出来的簇密度不一,或有很多离群值(outliers),这时候考虑使用密度聚类。
11.1.1.4 K-means 中常用的距离度量?
K-means中比较常用的距离度量是欧几里得距离和余弦相似度。
n维空间的欧几里得距离:
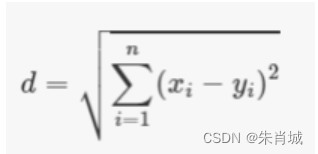
余弦相似度:余弦相似度是指两个向量夹角的余弦。两个方向完全相同的向量的余弦相似度为1,而两个彼此相对的向量的余弦相似度为-1

K-means是否会一直陷入选择质心的循环停不下来(为什么迭代次数后会收敛)?
从K-means的第三步我们可以看出,每回迭代都会用簇内点的平均值去更新簇中心,所以最终簇内的平方误差和(SSE, sum of squared error)一定最小。
11.1.1.5 为什么在计算K-means之前要将数据点在各维度上归一化?
因为数据点各维度的量级不同,例如:最近正好做完基于RFM模型的会员分群,每个会员分别有R(最近一次购买距今的时长)、F(来店消费的频率)和M(购买金额)。如果这是一家奢侈品商店,你会发现M的量级(可能几万元)远大于F(可能平均10次以下),如果不归一化就算K-means,相当于F这个特征完全无效。如果我希望能把常客与其他顾客区别开来,不归一化就做不到。
11.1.1.6 聚类和分类区别?
- 目的不同。聚类是一种无监督学习方法,目的是将数据对象自动分成不同的组或簇,这些簇是自然存在的,而不是人为定义的。分类则是一种监督学习方法,目的是根据已知的数据标签将新的数据对象分配到不同的类别中。
- 监督性不同。聚类不需要人工标注和预先训练分类器,类别在聚类的过程中自动生成。分类事先定义好类别,类别数不变,分类器需要由人工标注的分类训练语料训练得到。
- 结果性质不同。聚类结果是簇或类,这些簇或类是自然存在的,而不是人为定义的。分类结果是类别标签,这些类别标签是人为定义的。
- 应用场景不同。聚类适合于类别数不确定或不存在的场合,如市场细分、文本分类等。分类适合于类别或分类体系已经确定的场合,如邮件过滤、信用卡欺诈检测等。
- 算法复杂性不同。聚类算法通常比分类算法简单,因为聚类不需要预测新的数据点所属的类别。
- 结果解释不同。聚类分析的结果通常用于描述数据,衡量不同数据源间的相似性,以及把数据源分类到不同的簇中。分类分析的结果用于预测新的数据点所属的类别。
最大的不同在于:分类的目标是事先已知的,而聚类则不一样,聚类事先不知道目标变量是什么,类别没有像分类那样被预先定义出来。
11.1.2 Kmeans Vs KNN
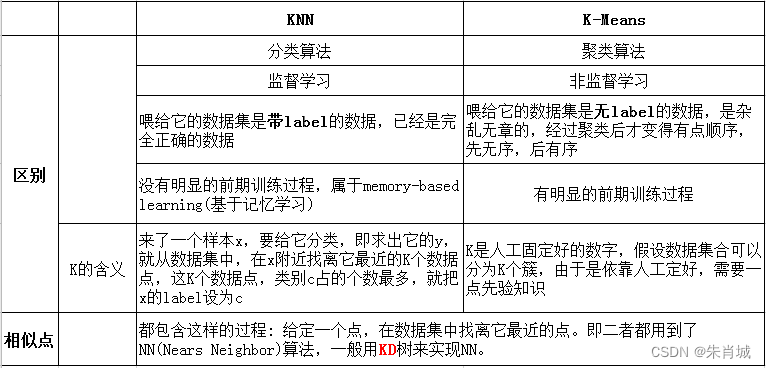
11.2 降维
定义:把一个多因素问题转化成一个较少因素(降低问题的维数)问题,而且较容易进行合理安排,找到最优点或近似最优点,以期达到满意的试验结果的方法。
11.2.1 主成分分析
PCA降维的原理: 无监督的降维(无类别信息)-->选择方差大的方向投影,方差越大所含的信息量越大,信息损失越少.可用于特征提取和特征选择。
PCA的计算过程
![]()
- 去平均值,即每一位特征减去各自的平均值
- 计算协方差矩阵
- 计算协方差矩阵的特征值与特征向量用(SVD,SVD比直接特征值分解计算量小)
- 对特征值从大到小排序
- 保留最大的个特征向量
- 将数据转换到个特征向量构建的新空间中
PCA推导
中心化后的数据在第一主轴u1方向上分布散的最开,也就是说在u1方向上的投影的绝对值之和最大(即方差最大),计算投影的方法就是将x与u1做内积,由于只需要求u1的方向,所以设u1是单位向量。

11.2.1.1 PCA其优化目标是什么?
最大化投影后方差 + 最小化到超平面距离
11.2.1.2 PCA 白化是什么?
通过 pca 投影以后(消除了特征之间的相关性),在各个坐标上除以方差(方差归一化)。
11.2.1.3 SVD奇异值分解
定义:有一个m×n的实数矩阵A,我们想要把它分解成如下的形式
![]()
其中U和V均为单位正交阵,即有![]() 和
和![]() ,U称为左奇异矩阵,V称为右奇异矩阵,Σ仅在主对角线上有值,称它为奇异值,其它元素均为0。上面矩阵的维度分别为
,U称为左奇异矩阵,V称为右奇异矩阵,Σ仅在主对角线上有值,称它为奇异值,其它元素均为0。上面矩阵的维度分别为![]() 。
。
11.2.1.4 为什么要用SVD进行降维?
1. 内存少:奇异值分解矩阵中奇异值从大到小的顺序减小的特别快,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上。
2.SVD可以获取另一个方向上的主成分,而基于特征值分解的只能获得单个方向上的主成分。
3.数值稳定性:通过SVD可以得到PCA相同的结果,但是SVD通常比直接使用PCA更稳定。PCA需要计算XTX的值,对于某些矩阵,求协方差时很可能会丢失一些精度。
11.2.2 LDA(线性判别式分析)
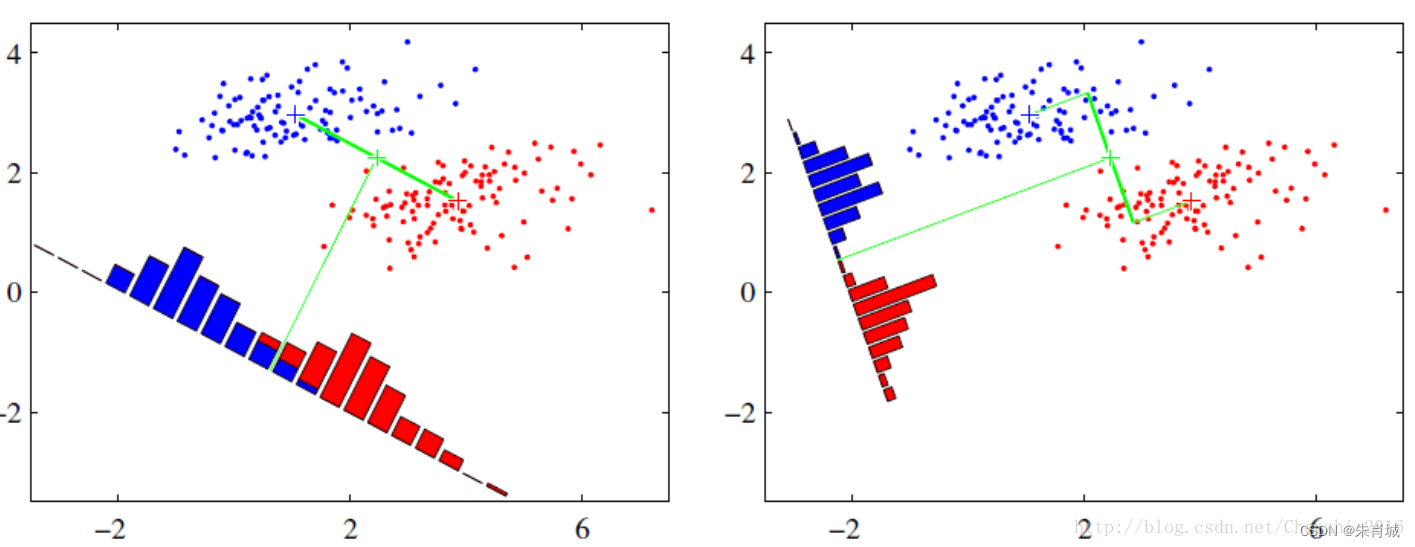
LDA降维的原理:LDA一种有监督的降维算法,它是将高维数据投影到低维上,并且要求投影后的数据具有较好的分类.(也就是说同一类的数据要去尽量的投影到同一个簇中去),投影后的类别内的方差小,类别间的方差较大.
理解: 数据投影在低维度空间后,投影点尽可能的接近,而不同类别的投影点群集的中心点彼此之间的离得尽可能大。
11.2.3 PCA vs SVD
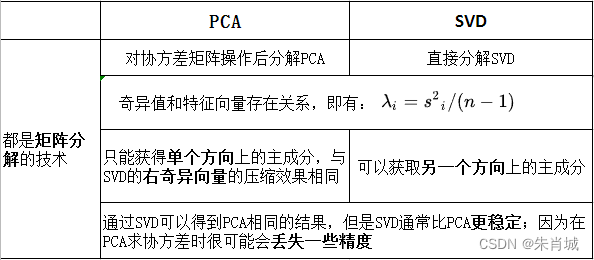
11.2.4 LDA vs PCA
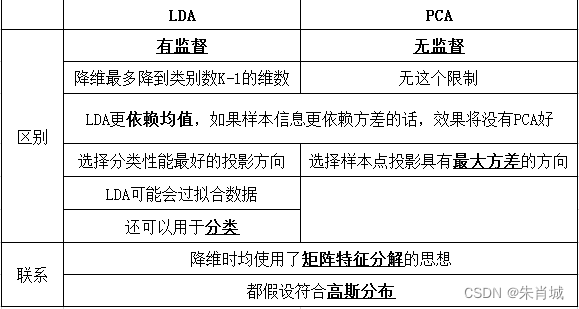
11.2.5 降维的作用是什么?
①降维可以缓解维度灾难问题
②降维可以在压缩数据的同时让信息损失最小化
③理解几百个维度的数据结构很困难,两三个维度的数据通过可视化更容易理解
11.2.6 矩阵的特征值和特征向量的物理意义是什么?
对于一个非方阵的矩阵A,它代表一个多维空间里的多个数据。求这个矩阵A的协方差阵Cov(A,A’),得到一个方阵B,求的特征值,就是求B的特征值,它就是代表矩阵A的那些数据,在那个多维空间中,各个方向上分散的一个度量(即理解为它们在各个方向上的特征是否明显,特征值越大,则越分散,也就是特征越明显),而对应的特征向量:是它们对应的各个方向。
(协方差:用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。)
11.2.7 维度灾难是什么?为什么要关心它?
- 维度灾难的一个主要后果是使分类器过拟合,其次使得样本在搜索空间(解释:目前本人将搜索空间理解为样本特征空间)的分布变得不均匀。
- 在特征数增加到一定数量后,继续添加新的特征会导致分类器的性能下降,这种现象称为“维度灾难”(The Curse of Dimensionality)。
解决方法:
降维算法:将高维数据转换为低维数据,并保留数据的关键信息,如PCA、LDA、MDS
特征选择:从原始数据中选取最具代表性的特征,并保留相对较少的特征,如卡方检验、信息熵
集成学习:将多个学习器进行有效的集成,以提高算法的预测准确度和鲁棒性,如随机森林、Adaboost等。