随想录日记part13

$time：$ 2024.03.06

---

---

主要内容：今天的主要内容是二叉树的第二部分哦，主要有层序遍历；翻转二叉树；对称二叉树。

• 102.二叉树的层序遍历
• 226.翻转二叉树
• 101. 对称二叉树

---

---

Topic1二叉树的层序遍历

题目： 给你二叉树的根节点 $root$ ，返回其节点值的层序遍历。 （即逐层地，从左到右访问所有节点）。

示例：

输入： $root=[3,9,20,null,null,15,7]$
输出： $[[3],[9,20],[15,7]]$

**思路：**层序遍历是一层一层去遍历二叉树，符合先进先出的规则，即图论中的广度优先遍历思路，所以这道题目我们需要辅助的队列来实现层序遍历。其遍历的动画可以观看下面的动画：

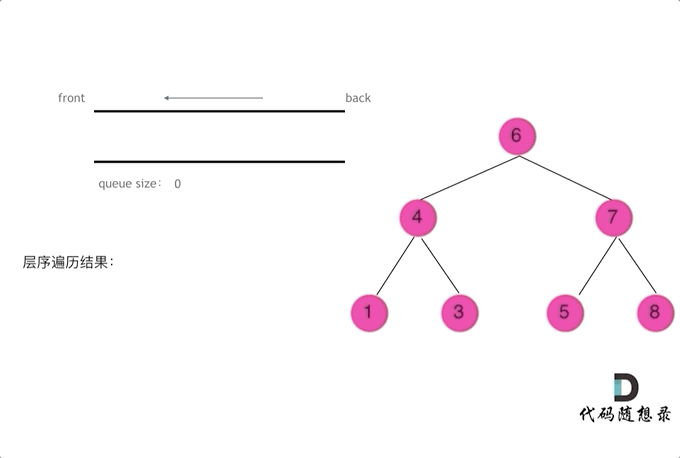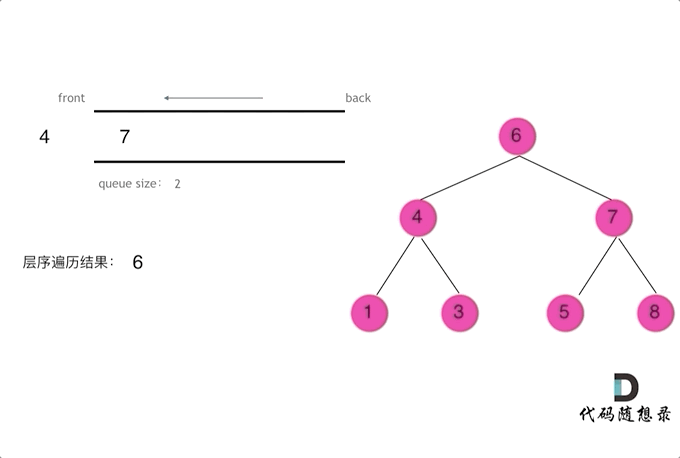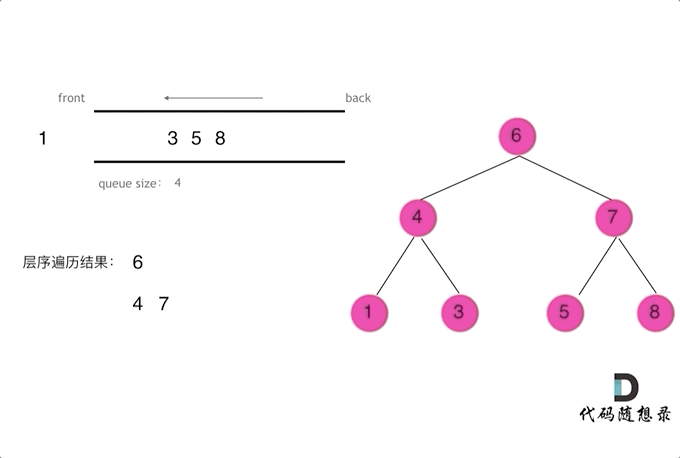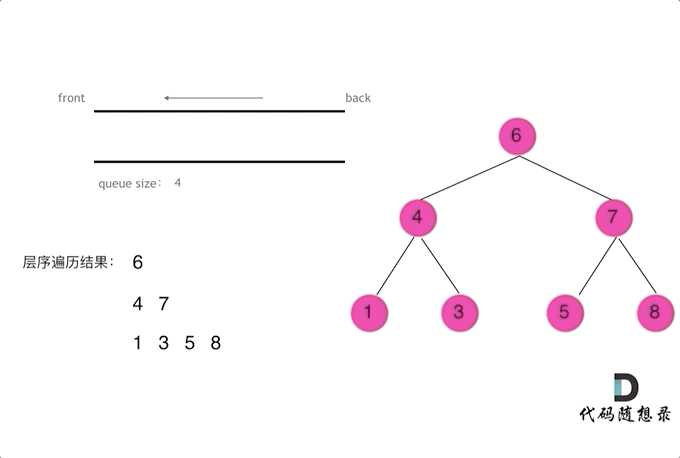
下面给出两种层序遍历的写法：

class Solution {
    // 定义一个记录组后输出的数组
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        //levelOrder_queue(root);
        levelOrder_queue_pro(root,0);
        return resList;
    }

    // 使用栈辅助进行层次遍历
    private void levelOrder_queue(TreeNode root) {
        if (root == null)
            return;
        // 创建辅助队列
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.offer(root);
        while (!q.isEmpty()) {
            List<Integer> tem = new ArrayList<Integer>();
            int length = q.size();
            while (length > 0) {
                TreeNode t = q.poll();
                tem.add(t.val);
                if (t.left != null)
                    q.offer(t.left);
                if (t.right != null)
                    q.offer(t.right);
                length--;
            }
            resList.add(tem);
        }
    }

    //使用递归的方法
    private void levelOrder_queue_pro(TreeNode root,int deep){
        if(root==null) return;
        deep++;
        if(resList.size()<deep){
            //当层级增加时，list的Item也增加，利用list的索引值进行层级界定
            List<Integer> tem = new ArrayList<Integer>();
            resList.add(tem);
        }
        resList.get(deep-1).add(root.val);
        levelOrder_queue_pro(root.left,deep);
        levelOrder_queue_pro(root.right,deep);

    }
}

上面的两种写法务必要记住。

---

---

Topic2翻转二叉树

**题目：**给你一棵二叉树的根节点 $root$ ，翻转这棵二叉树，并返回其根节点。
示例：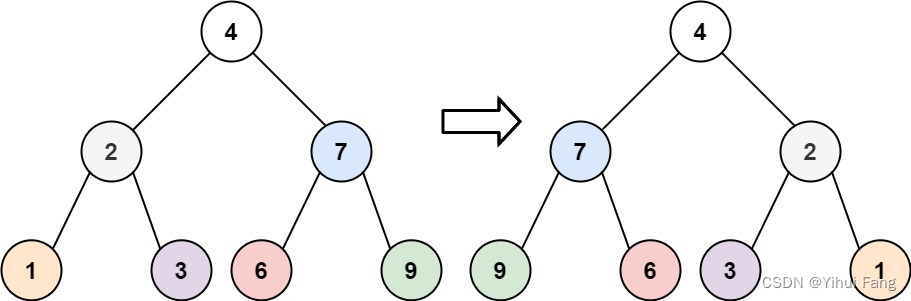
输入： $root=[4,2,7,1,3,6,9]$
输出： $[4,7,2,9,6,3,1]$

**思路：**整个树的翻转主要有两种思路：

• 递归
• 迭代

• 递归法：写好递归是要有三个关键点注意的：
  1.确定参数和返回值

TreeNode transTree(TreeNode root);

2.确定中止条件

 if(root==null)return null;

3.确定单层递归逻辑
我的代码是前序遍历，先反转左右子树，然后进行交换左右孩子节点

		TreeNode b=transTree(root.right);
        TreeNode a=transTree(root.left);
        tem.left=b;
        tem.right=a;

完整的 $java$ 代码如下：

class Solution {
    public TreeNode invertTree(TreeNode root) {
        return transTree(root);
    }

    private TreeNode transTree(TreeNode root) {
        TreeNode tem = root;
        if (tem == null)
            return null;
        TreeNode b = transTree(root.right);
        TreeNode a = transTree(root.left);
        tem.left = b;
        tem.right = a;
        return root;
    }
}

---

• 迭代法：能够使用递归的方法都能使用栈来实现：
  如下面代码实现：

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root==null)return root;
        //建立栈
        Stack<TreeNode> stack=new Stack<TreeNode>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode tem=stack.pop();
            transpoint(tem);
            if(tem.right!=null)stack.push(tem.right);
            if(tem.left!=null)stack.push(tem.left);
        }
        return root;
    }

    private void transpoint(TreeNode root){
        if(root==null)return;
        else{
            TreeNode t=root.left;
            root.left=root.right;
            root.right=t;
        }
    }
}

---

---

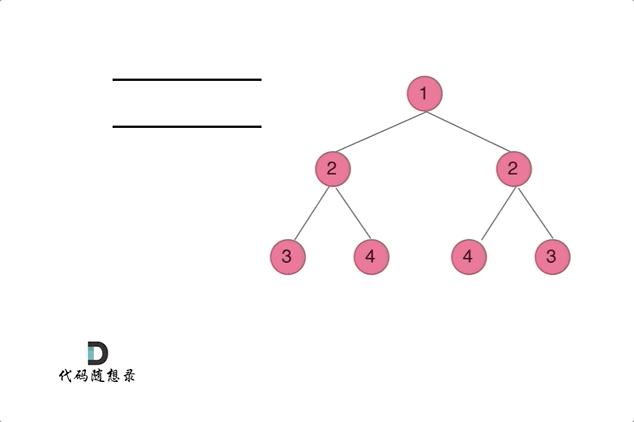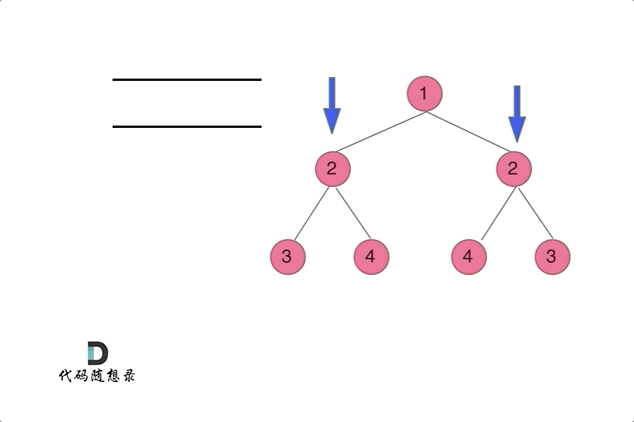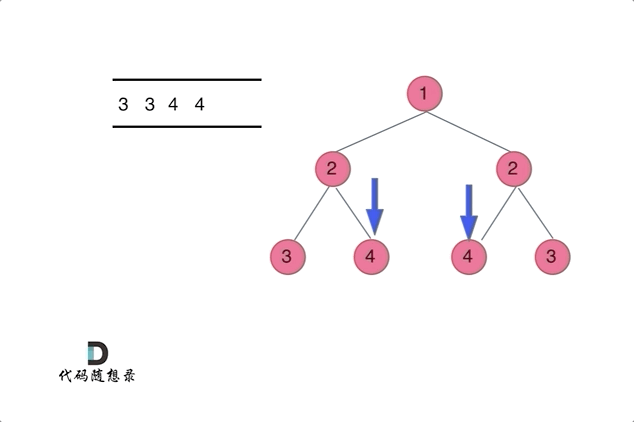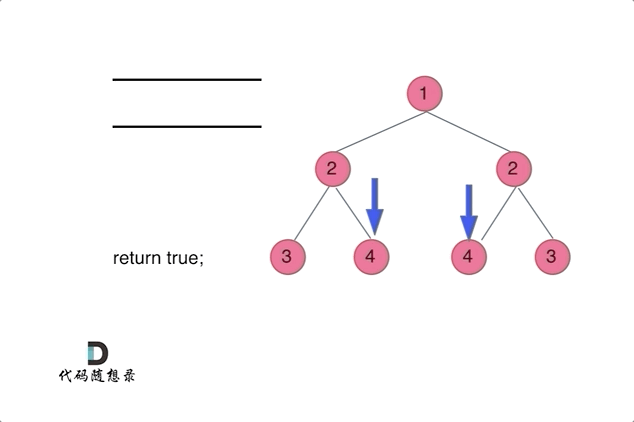
Topic3对称二叉树

**题目：**给你一个二叉树的根节点 $root$ ， 检查它是否轴对称。
示例：

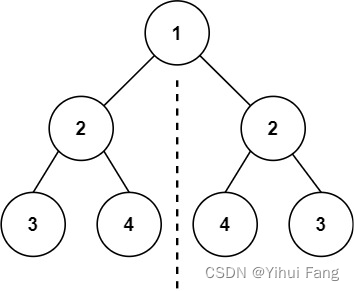
输入： $root=[1,2,2,3,4,4,3]$
输出： $true$

思路：
后序遍历的递归法以及迭代法

递归法：

class Solution {// 递归法
    public boolean isSymmetric(TreeNode root) {
        if (root == null)
            return true;
        else
            return isSame(root.left, root.right);
    }

    private boolean isSame(TreeNode left, TreeNode right) {
        if (left == null && right != null)
            return false;
        else if (left != null && right == null)
            return false;
        else if (left == null && right == null)
            return true;
        else {
            boolean a = isSame(left.left, right.right);
            boolean b = isSame(left.right, right.left);
            return (a && b);
        }
    }
}

迭代法：

代码实现如下：

class Solution {// 使用队列辅助实现的迭代法
    public boolean isSymmetric(TreeNode root) {
        if (root == null)
            return true;
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offerFirst(root.left);// 将左子树头节点压入
        queue.offerLast(root.right);// 将右子树头节点压入
        while (!queue.isEmpty()) {
            TreeNode left = queue.pollFirst();
            TreeNode right = queue.pollLast();
            if (left == null && right == null)
                continue;
            if (left == null || right == null || left.val != right.val)
                return false;
            queue.offerFirst(left.left);
            queue.offerLast(right.right);
            queue.offerFirst(left.right);
            queue.offerLast(right.left);
        }
        return true;
    }
}