本专栏内容为：递归，搜索与回溯算法专栏。 通过本专栏的深入学习，你可以了解并掌握算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：递归搜索回溯专栏
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

题目来源

本题来源为：

Leertcode 50.Pow(x,n)

题目描述

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xⁿ ）。

算法原理

解法一：暴力+循环
看到这个题很容易就想到暴力解决。
例如2的10次方，我们就让循环10次，每次进行相乘，但这么做肯定会超时。

解法二：快速幂

快速幂是一个算法，有两种解决办法：

1. 递归
2. 循环
   这里我们讲解递归的方法：

例子1：3¹⁶的计算：

我们将16次方拆成两个8次方相乘，将8次方拆成两个4次方相乘，依次内推，当数是1次方的时候，我们拆成3的0次方。而这个0次方也将作为我们的出口，因为0次方在拆也还是0次方。

例子2：3²¹

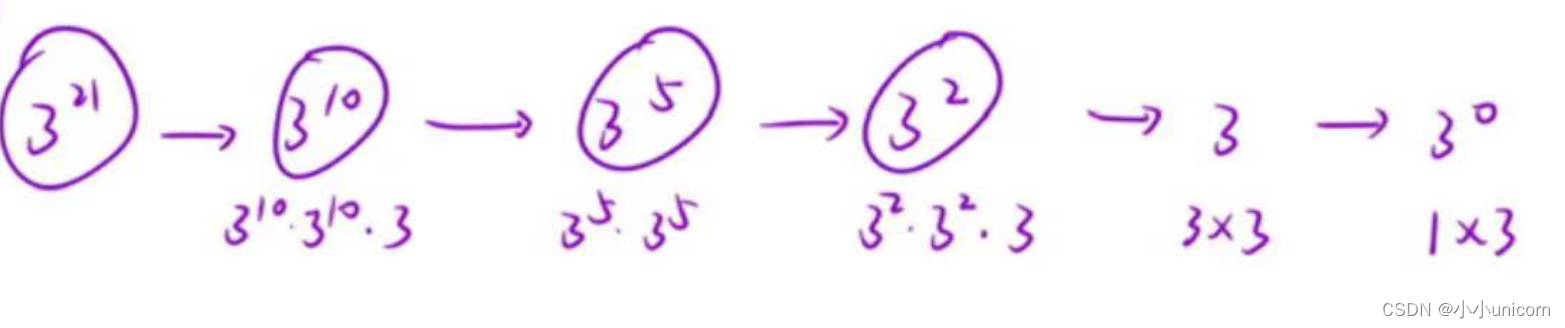
首先将21次方拆成一半，除不尽，就在多乘以本身这个值，依次内推。

分析到这，我们其实已经发现这道题相同的子问题了，那么就用递归来解决：

相同子问题->函数头

本题相同子问题很好分析，就是计算xⁿ;

只关心每个子问题做了什么->函数体

那么子问题应该做什么呢？

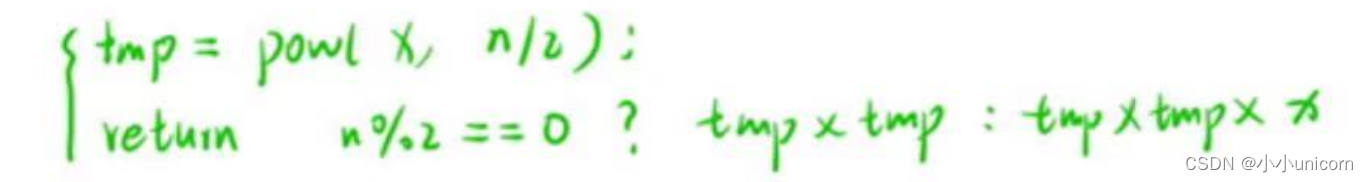
分两步：

1. 先计算x的一半次方的值，将其保存起来。
2. 看这个结果能否被除尽，能除尽直接返回，不能除尽就在这个值的基础上再乘一个x.

函数出口

写递归一定要写出口，防止造成死循环。
本题函数出口就是当n==0的时候，返回1即可。

细节问题：

其实分析到返回值，就可以代码实现，但是还要注意一下细节问题。
因为n有可能会无穷大也有可能会无穷小或者为负数：

1. 当为负数时：
   
   我们在计算完结果跟1进行相除，变成分数。

2. 当为无穷小时：
   
   我们将其进行强转即可。

代码实现

class Solution 
{
public:
    double myPow(double x, int n) 
    {
        //注意判断是否为负数以及数据溢出进行强转
        return n<0?1.0/pow(x,-(long long)n):pow(x,n);
    }
    double pow(double x,long long n)
    {
        //递归出口：
        if(n==0)
        return 1.0;
        //保存值
        double tmp=pow(x,n/2);
        //判断是否除尽
        return n %2 ==0?tmp*tmp:tmp*tmp*x;
    }
};