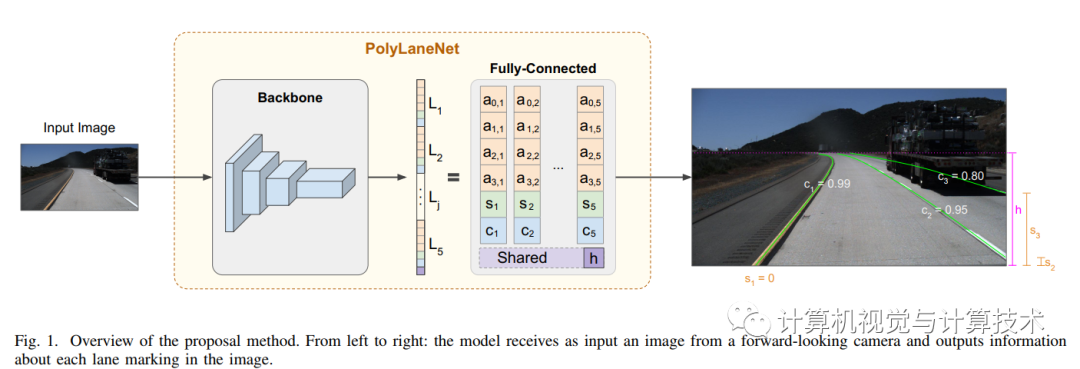
文章目录
- 泛函
- 泛函定义
- 泛函的变分
- 自变量的变分
- 泛函相近
- 泛函距离
- 泛函的连续性
- 线性泛函
- 泛函的变分
- 泛函的极值
- 泛函极值的定义
- 泛函的极值
- 泛函极值条件
泛函
泛函定义
对于某一类函数集合
{
x
(
t
)
}
\{x(t)\}
{x(t)} 中的每一个函数
x
(
t
)
x(t)
x(t), 在映射关系
J
J
J 下均有一个确定的数与之对应,则称
J
J
J 为依赖于函数
x
(
t
)
x(t)
x(t) 的泛函,记作
J
=
J
[
x
(
.
)
]
=
J
[
x
(
t
)
]
J=J[x(.)]=J[x(t)]
J=J[x(.)]=J[x(t)]
注:泛函与函数的区别
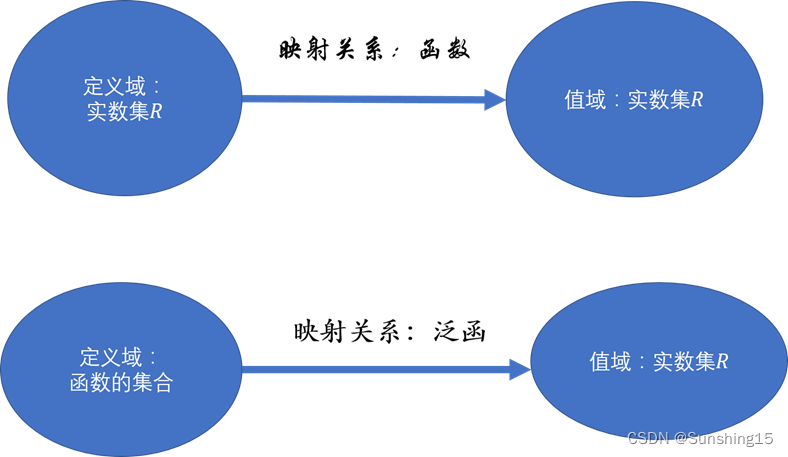
泛函即为以函数为自变量的一种映射到实数域的映射关系。而函数则是以某一实数为自变量映射到实数域的映射关系。这里的
J
[
x
(
t
)
]
J[x(t)]
J[x(t)]可理解为整条曲线
x
(
t
)
x(t)
x(t) 在映射关系
J
J
J 下对应一个实数值。
泛函的变分
自变量的变分
- 宗量:若函数 x ( t ) x(t) x(t) 是映射关系 J J J 的自变量函数,则称 x ( t ) x(t) x(t) 为泛函 J [ x ( t ) ] J[x(t)] J[x(t)] 的宗量函数。
- 宗量的变分:宗量的变分是指在同一函数类中的两个宗量函数间的差,即: δ x ( t ) = x ( t ) − x ∗ ( t ) . \delta x(t)=x(t)-x^*(t). δx(t)=x(t)−x∗(t).
泛函相近
- 零阶相近
当宗量的变分 δ x ( t ) \delta x(t) δx(t) 的绝对值对于 x ( t ) x(t) x(t) 定义域中的一切 t t t 都很小时,称函数 x ( t ) x(t) x(t) 与 x ∗ ( t ) x^*(t) x∗(t) 是接近的,也称为零阶相近。 - 一阶相近
当宗量的变分 δ x ( t ) \delta x(t) δx(t) 的绝对值以及 δ x ( t ) \delta x(t) δx(t) 的一阶导数的绝对值对于 x ( t ) x(t) x(t) 定义域中的一切 t t t 都很小,则称函数 x ( t ) x(t) x(t) 与 x ∗ ( t ) x^*(t) x∗(t) 是一阶相近的。 - K阶相近
当 ∣ x ( t ) − x ∗ ( t ) ∣ |x(t)-x^*(t)| ∣x(t)−x∗(t)∣, ∣ x ˙ ( t ) − x ˙ ∗ ( t ) ∣ |\dot{x}(t)-\dot{x}^*(t)| ∣x˙(t)−x˙∗(t)∣, … \ldots …, ∣ x ( k ) ( t ) − x ∗ ( k ) ( t ) ∣ |x^{(k)}(t)-x^{*(k)}(t)| ∣x(k)(t)−x∗(k)(t)∣ 对一切 t t t 都很小时, 称函数 x ( t ) x(t) x(t) 与 x ∗ ( t ) x^*(t) x∗(t) 是 k k k 阶相近的。
泛函距离
- 零阶距离
在连续函数全体组成的函数空间 C [ a , b ] C[a,b] C[a,b]中,泛函自变量的距离可定义为 d [ x ( t ) , x ∗ ( t ) ] = max a ≤ t ≤ b { x ( t ) − x ∗ ( t ) } d[x(t),x^*(t)]=\displaystyle \max_{a\leq t\leq b}\{x(t)-x^*(t)\} d[x(t),x∗(t)]=a≤t≤bmax{x(t)−x∗(t)} -
k
k
k 阶距离
由在区间 [ a , b ] [a,b] [a,b]上连续且具有连续的 k k k 阶导数的函数的全体构成的函数空间 C k [ a , b ] C^{k}[a,b] Ck[a,b] 中,任意两个函数间的 k k k阶距离定义为 d [ x ( t ) , x ∗ ( t ) ] = max a ≤ t ≤ b { ∣ x ( t ) − x ∗ ( t ) ∣ , ∣ x ˙ ( t ) − x ˙ ∗ ( t ) ∣ , … , ∣ x ( k ) ( t ) − x ∗ ( k ) ( t ) ∣ } d[x(t),x^*(t)]=\displaystyle \max_{a\leq t\leq b}\{|x(t)-x^*(t)|,|\dot{x}(t)-\dot{x}^*(t)|,\ldots,|x^{(k)}(t)-x^{*(k)}(t)|\} d[x(t),x∗(t)]=a≤t≤bmax{∣x(t)−x∗(t)∣,∣x˙(t)−x˙∗(t)∣,…,∣x(k)(t)−x∗(k)(t)∣}
泛函的连续性
对于任意给定的正数
ε
\varepsilon
ε, 总可以找到一个正数
δ
\delta
δ, 使得当
d
(
x
,
x
∗
)
<
δ
d(x, x^*)<\delta
d(x,x∗)<δ 时, 有
∣
J
[
x
(
t
)
]
−
J
[
x
∗
(
t
)
]
∣
<
ε
|J[x(t)]-J[x^*(t)]|<\varepsilon
∣J[x(t)]−J[x∗(t)]∣<ε 则称泛函
J
[
x
(
t
)
]
J[x(t)]
J[x(t)] 在
x
∗
(
t
)
x^*(t)
x∗(t) 处是连续的。其中,
d
(
x
,
x
∗
)
=
max
a
≤
t
≤
b
∣
x
(
t
)
−
x
∗
(
t
)
∣
d(x, x^*)=\displaystyle \max_{a\leq t \leq b}|x(t)-x^*(t)|
d(x,x∗)=a≤t≤bmax∣x(t)−x∗(t)∣。根据所采用的泛函自变量之间的距离的定义方式的不同,可分别定义泛函的零阶连续以及
k
k
k 阶连续泛函。
Lemma 1: 如果函数
F
(
t
)
F(t)
F(t) 在区间
[
t
0
,
t
f
]
[t_0, t_f]
[t0,tf] 上是连续的, 而且对于只满足某些一般条件的任意选定的函数
η
(
t
)
\eta(t)
η(t) 有
∫
t
0
t
f
F
(
t
)
η
(
t
)
d
t
=
0
\displaystyle\int_{t_0}^{t_f}F(t)\eta(t)dt=0
∫t0tfF(t)η(t)dt=0, 则在区间
[
t
0
,
t
f
]
[t_0, t_f]
[t0,tf] 上有
F
(
t
)
=
0
F(t)=0
F(t)=0。
线性泛函
连续泛函 J [ x ( t ) ] J[x(t)] J[x(t)] 如果满足如下两个条件: J [ x 1 ( t ) + x 2 ( t ) ] = J [ x 1 ( t ) ] + J [ x 2 ( t ) ] J[x_1(t)+x_2(t)]=J[x_1(t)]+J[x_2(t)] J[x1(t)+x2(t)]=J[x1(t)]+J[x2(t)] J [ C x ( t ) ] = C J [ x ( t ) ] J[Cx(t)]=CJ[x(t)] J[Cx(t)]=CJ[x(t)]其中 C C C 为常数, 则 J [ x ( t ) ] J[x(t)] J[x(t)] 为线性泛函。
泛函的变分
- 泛函的增量
由自变量函数 x ( t ) x(t) x(t) 的变分 δ x ( t ) \delta x(t) δx(t) 引起泛函 J [ x ( t ) ] J[x(t)] J[x(t)] 的增量 Δ J = J [ x ∗ ( t ) + δ x ( t ) ] − J [ x ∗ ( t ) ] \Delta J=J[x^*(t)+\delta x(t)]-J[x^*(t)] ΔJ=J[x∗(t)+δx(t)]−J[x∗(t)] 为泛函 J [ x ( t ) ] J[x(t)] J[x(t)] 的增量。 - 泛函的变分
当宗量函数 x ( t ) x(t) x(t) 有变分时,泛函 J [ x ( t ) ] J[x(t)] J[x(t)] 的增量 Δ J [ x ( t ) ] \Delta J[x(t)] ΔJ[x(t)] 可表示为 Δ J = J [ x ∗ ( t ) + δ x ( t ) ] − J [ x ( t ) ] = d J d x ∣ x ∗ δ x + 1 2 d 2 J d x 2 ∣ x ∗ ( δ x ) 2 + R , \Delta J=J[x^*(t)+\delta x(t)]-J[x(t)]=\frac{dJ}{dx}|_{x^*}\delta x+\frac{1}{2}\frac{d^2J}{dx^2}|_{x^*}(\delta x)^2+R, ΔJ=J[x∗(t)+δx(t)]−J[x(t)]=dxdJ∣x∗δx+21dx2d2J∣x∗(δx)2+R, 其中 Δ J \Delta J ΔJ 的线性部分称为泛函的变分,记作 δ J \delta J δJ,即 δ J = d J d x ∣ x ∗ δ x , \delta J=\frac{dJ}{dx}|_{x^*}\delta x, δJ=dxdJ∣x∗δx,换句话说即为泛函的变分是泛函增量的线性主部。
Lemma 2: 泛函的变分 δ J = ∂ ∂ α J [ x ( t ) + α δ x ( t ) ] ∣ α = 0 \delta J=\frac{\partial}{\partial \alpha}J[x(t)+\alpha \delta x(t)]|_{\alpha=0} δJ=∂α∂J[x(t)+αδx(t)]∣α=0
Example 1: 计算泛函
J
=
∫
0
1
x
2
(
t
)
d
t
J=\displaystyle \int_0^1x^2(t)dt
J=∫01x2(t)dt 的变分。
δ
J
=
∂
∂
α
J
[
x
(
t
)
+
α
δ
x
(
t
)
]
∣
α
=
0
=
∂
∂
α
∫
0
1
[
x
(
t
)
+
α
δ
x
(
t
)
]
2
d
t
∣
α
=
0
=
∫
0
1
2
[
x
(
t
)
+
α
δ
x
(
t
)
]
δ
x
(
t
)
d
t
∣
α
=
0
=
∫
0
1
2
x
(
t
)
δ
x
(
t
)
d
t
\begin{aligned} \delta J&=\frac{\partial}{\partial \alpha}J[x(t)+\alpha\delta x(t)]|_{\alpha=0}\\ &=\frac{\partial}{\partial \alpha}\displaystyle\int_0^1[x(t)+\alpha\delta x(t)]^2dt|_{\alpha=0}\\ &=\displaystyle\int_0^12[x(t)+\alpha \delta x(t)]\delta x(t)dt|_{\alpha=0}\\ &=\displaystyle\int_0^12x(t)\delta x(t)dt \end{aligned}
δJ=∂α∂J[x(t)+αδx(t)]∣α=0=∂α∂∫01[x(t)+αδx(t)]2dt∣α=0=∫012[x(t)+αδx(t)]δx(t)dt∣α=0=∫012x(t)δx(t)dt
泛函的极值
泛函极值的定义
如果泛函 J [ x ( t ) ] J[x(t)] J[x(t)] 在 x ( t ) = x ∗ ( t ) x(t)=x^*(t) x(t)=x∗(t) 的邻域内,其增量 Δ J = J [ x ( t ) − x ∗ ( t ) ] = J [ x ( t ) ] − J [ x ∗ ( t ) ] ≥ 0 \Delta J=J[x(t)-x^*(t)]=J[x(t)]-J[x^*(t)]\geq 0 ΔJ=J[x(t)−x∗(t)]=J[x(t)]−J[x∗(t)]≥0 或 Δ J = J [ x ( t ) − x ∗ ( t ) ] = J [ x ( t ) ] − J [ x ∗ ( t ) ] ≤ 0 \Delta J=J[x(t)-x^*(t)]=J[x(t)]-J[x^*(t)]\leq 0 ΔJ=J[x(t)−x∗(t)]=J[x(t)]−J[x∗(t)]≤0 则称泛函 J [ x ( t ) ] J[x(t)] J[x(t)] 在 x ( t ) = x ∗ ( t ) x(t)=x^*(t) x(t)=x∗(t) 有极小值或极大值。
泛函的极值
- 强极值:如果 J [ x ∗ ( t ) ] J[x^*(t)] J[x∗(t)] 是在与 x ( t ) x(t) x(t) 仅仅具有零阶接近度的曲线 x ( t ) x(t) x(t) 的泛函中比较得出的极值,称为强极值。
- 弱极值:如果 J [ x ∗ ( t ) ] J[x^*(t)] J[x∗(t)] 是在与 x ( t ) x(t) x(t) 具有一阶或一阶以上接近度的曲线 x ( t ) x(t) x(t) 的泛函中比较得出的极值,称为弱极值。
泛函极值条件
- 必要条件
若可微泛函 J [ x ( t ) ] J[x(t)] J[x(t)] 在曲线 x ( t ) = x ∗ ( t ) x(t)=x^*(t) x(t)=x∗(t) 达到极值,则泛函 J [ x ( t ) ] J[x(t)] J[x(t)] 在 x ( t ) = x ∗ ( t ) x(t)=x^*(t) x(t)=x∗(t) 上的变分等于零,即 δ J [ x ∗ ( t ) ] = 0 \delta J[x^*(t)]=0 δJ[x∗(t)]=0。
证明:对于任意给定的 δ x ( t ) \delta x(t) δx(t) 来说, J [ x ∗ ( t ) + α δ x ( t ) ] J[x^*(t)+\alpha \delta x(t)] J[x∗(t)+αδx(t)] 是实变量 α \alpha α 的函数。泛函 J [ x ( t ) ] J[x(t)] J[x(t)] 在 x ∗ ( t ) x^*(t) x∗(t) 达到极值,即函数 J [ x ∗ ( t ) + α δ x ( t ) ] J[x^*(t)+\alpha \delta x(t)] J[x∗(t)+αδx(t)] 在 α = 0 \alpha=0 α=0 时达到极值,所以它的导数在 α = 0 \alpha=0 α=0 时应为零,即 ∂ ∂ α J [ x ∗ ( t ) + α δ x ( t ) ] ∣ α = 0 = 0 \frac{\partial}{\partial\alpha}J[x^*(t)+\alpha\delta x(t)]|_{\alpha=0}=0 ∂α∂J[x∗(t)+αδx(t)]∣α=0=0 由变分引理可知 ∂ ∂ α J [ x ∗ ( t ) + α δ x ( t ) ] ∣ α = 0 = δ J [ x ∗ ( t ) ] = 0 \frac{\partial}{\partial\alpha}J[x^*(t)+\alpha\delta x(t)]|_{\alpha=0}=\delta J[x^*(t)]=0 ∂α∂J[x∗(t)+αδx(t)]∣α=0=δJ[x∗(t)]=0。得证。 - 充要条件
设可微泛函 J ( x ) J(x) J(x) 存在二次变分, 则在 x = x ∗ x=x^* x=x∗ 处达到极小值的充要条件为: δ J ( x ∗ ) = 0 , δ 2 J ( x ∗ ) > 0. \delta J(x^*)=0,\delta^2J(x^*)>0. δJ(x∗)=0,δ2J(x∗)>0. 同理,设可微泛函 J ( x ) J(x) J(x) 存在二次变分,则在 x = x ∗ x=x^* x=x∗ 处存在极大值的充要条件为: δ J ( x ∗ ) = 0 , δ 2 J ( x ∗ ) < 0. \delta J(x^*)=0,\delta^2J(x^*)<0. δJ(x∗)=0,δ2J(x∗)<0.